Dandelin Spheres and the Conic Sections

Apostol's ice-cream-cone proof — click image for the entire page.

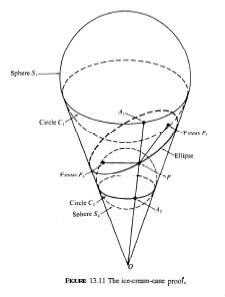
In high school, the fact that the conic sections are derived from the cone was mentioned in passing, but they were defined in the plane by their equations and tied to their focal properties. So seeing the Dandelin spheres in Apostol fifty years ago was a revelation, effective and surpassingly elegant. He called it the ice-cream-cone proof, virtually a proof by picture that a cone cut obliquely by a plane results in an ellipse as defined by its focal property. The book in question is Calculus, Volume I, by Tom Apostol^[1], among my top three favorite books all-time, first for math. Originally published by Blaisdell in 1961 in large format — unusual in that day, 10" x 7" — Apostol did not condescend, but did not batter you either. After many miles, you look back on an old teacher and think, he did that perfectly, not fully comprehending yourself that he taught you once and for all what mathematical taste is one day in 1965. The book is deeply informed by history altogether apart from the historical introductions, economical and suggestive of hidden depths as they are. Some subjects are one with their own history, philosophy for example, and math is a little like that.

In the first few pages, he develops Archimedes' method of exhaustion, pointing out quite rightly that calculus originated with the old master of thought (that is what Archimedes means). Then he takes up mathematical induction and puts the real numbers on a firm foundation, including the Archimedean property (!). He has you proving the Binet formula for the Fibonacci numbers and Cauchy-Schwarz by page 35, both as exercises and eminently approachable with his guidance. He takes up integration before differentiation in keeping with the historical development and rolls out analytic geometry in a particularly effective way, dot and cross products and the rest, including in 3D. I've reached for my Apostol many times over the years when wrestling with computer graphics. Old calculus teachers could say with more authority, but this book may have had considerable influence on calculus texts in the United States over this period; like George Thomas's old classic, Apostol is still in print, and not in the 13^th edition either — he did it right pretty much from the start.

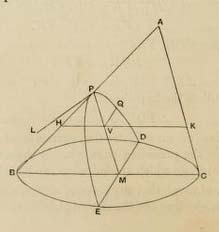
Of course the ancients brought the conic sections down from the cone to the plane, and quickly if Apollonius is any guide. The image here is from Heath's edition of his Conic Sections, Proposition I, 11, concerning the parabola. Apollonius uses simple considerations of parallelism and similar triangles to prove that:

\[ QV^2 = {PL \cdot PV}, \]

where \( QV \) is the abscissa, \( PV \) the ordinate, and \( PL \) the constant latus rectum. The ideas of ordinate and abscissa played a prominent role in Apollonius, not those words and not in the sense of modern Cartesian geometry, but the ideas themselves — see Heath's discussion at those links. Befitting an ancient Greek geometer, this expression actually equates the area of a square on the left with the area of a rectangle on the right. The latus rectum of the parabola plays a big role; in the plane, it can be identified with the line segment through the focus perpendicular to the axis and connecting opposite points on the parabola (and similarly for ellipse and hyperbola). In modern notation, Apollonius's equation reads \( y^2 = ax \), our equation for a parabola.

Proposition I, 12 and I, 13 bring down the hyperbola and ellipse, respectively, and the modern equations jump out right away. Descartes and his editor and commenter van Schooten posed and solved a similar problem for the ellipse, deriving the equation much as we would. Gary Stoudt does a fine job recapitulating Apollonius at the MAA site.

Germinal Pierre Dandelin was born on 23 Germinal, Year II (April 12, 1794), presumably into a revolutionary family; his father was French, his mother Belgian. He volunteered to fight for the Napoleonic regime as a teenager and took part in the revolution of 1830 according to Dirk Struik, an extensive uprising leading to Belgian independence from the Netherlands. A military engineer by profession, he participated broadly in the science and culture of his time, writing a successful libretto for an opera with Quetelet. In 1822, he wrote Mémoire sur quelques propriétés remarquables de la focale parabolique^[2], explaining how to derive the focal properties of the conic sections from their definitions as sections on the cone. He considers the ellipse in the first few paragraphs, as follows:

Cut a right circular cone by an oblique plane in such a way that the intersection is a closed curve (the plane intersects just one nap of the cone and is not parallel to any of the lines running down the cone from the vertex); by definition, the intersection of cone and plane is an ellipse. Fit a tiny sphere tightly inside the cone towards the vertex above the cutting plane; its intersection with the cone will be circle. Gradually increase the size of the sphere, keeping it tangent to the inside of the cone, walking it down the cone until the sphere intersects the plane below at a single point, \( F_1 \) in the figure. Start similarly with a very large sphere under the plane, gradually decreasing its size and moving it up the cone until it touches the plane above at a single point \( F_2 \). When that configuration is reached, both spheres are tangent to the cutting plane and to the cone; the intersection of the cone with the smaller circle above is labelled \( k_1 \), and the intersection of the cone with the larger circle below is labelled \( k_2 \),

Let \( P \) be any point on the ellipse. Draw a line from \( P \) through the cone up to its vertex \( S \) and let \( P_1 \) be its point of intersection with circle \( k_1 \). Connect \( P \) to \( F_1 \), line segment \( PF_1 \) being entirely in the cutting plane. Then:

\[ PF_1 = PP_1, \]

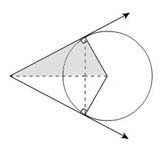
because each represents a segment tangent to the small sphere from the external point \( P \). Such tangent segments are equal as shown by the figure here, because the tangents are perpendicular to the circle and the gray triangle is congruent to the matching one just underneath it; the extension to a sphere is immediate. Stare at the picture until you see it, the entire proof is right there. In exactly the same way:

\[ PF_2 = PP_2,. \]

because both those segments are tangent to the large sphere from external point \( P \). But \( PP_1 + PP_2 \) is constant, just being the slant distance between the parallel planes containing circles \( k_1 \) and \( k_2 \). It follows that \( PF_1 + PF_2 \) is constant, which is the focal property of the ellipse with foci \( F_1 \) and \( F_2 \):

\[ {PF_1 + PF_2} = {PP_1 + PP_2} = \text{ constant}. \]

Those three equations obtain as the point \( P \) moves all around the ellipse. The construction even identifies the foci as the points of tangency of the spheres with the cutting plane; they are called Dandelin spheres. In Dandelin's words, changing only the labels for points:

Germinal Dandelin

Mais cette dernière quantité est constante, puisqu’elle dépend seulement de l’angle au centre du cône et de la position des deux sphères, et que ces trois élémens sont indépendans de la position du point \( P \) sur le contour de la section; donc on peut en conclure que la somme des rayons vecteurs, menés des points \( F1 \) et \( F2 \) à un point quelconque de cette section, est constante.

But this quantity is constant, since it only depends on the angle of taper and the position of the two spheres, and these three elements are independent of the position of the point \( P \) on the contour of the section; so we can conclude that the sum of the radius vectors from the points \( F1 \) and \( F2 \) to any point of this section is constant.

Click image for larger version.

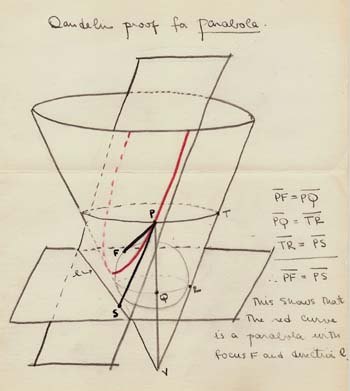
The parabola requires just one Dandelin sphere, as shown in my drawing from all those years ago, tucked away in Apostol. The cutting plane cuts down through the plane parallel to one of its generators, that is, line \( TRV \) running up the cone from the vertex. Drop a small sphere down the cone behind the plane as suggested by the picture, enlarging it until it fits snugly, tangent to the plane at point \( F \), which is going to be the focus.

The sphere intersects the cone in the small circle lower in the figure and parallel to the base of the cone. The horizontal plane is the plane of that circle, itself parallel to the base of the cone. The cutting plane and the horizontal plane intersect in line \( l \), which is going to be the parabola's directrix. Take any point \( P \) on the parabola and connect it to \( F \). Also connect \( P \) to the cone's vertex \( V \) by a line running down through the cone and intersecting the little circle at \( Q \). Draw the horizontal circle around the cone through \( P \); it's in the middle of the cone as pictured here and is parallel to the base of the cone and to the little circle lower on the cone. Let \( T \) be the point on this circle just opposite the cutting plane and likewise \( R \) is the point on the little circle opposite the cutting plane. Put otherwise, the cutting plane is parallel to line \( TRV \) thought of as a generator of the cone. Finally, draw a line from \( P \) down through the cutting plane and perpendicular to line \( l \), meeting line \( l \) at \( S \). Then:

\[ PF = PQ = TR = PS. \]

The first equality is because segments \( PF \) and \( PQ \) are tangent to the sphere from external point \( P \). The second inequality is because \( PQ \) and \( TR \) are each the slant distance between the two parallel circles along the cone. The third inequality is because \( TR \) and \( PS \) are parallel and represent the same slant distance between two parallel planes. In short, \( PF = PS \), the focus-directrix property of the parabola, where point of tangency \( F \) is the focus and line \( l \) is the directrix.

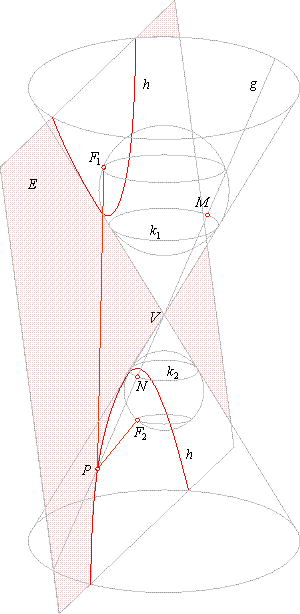
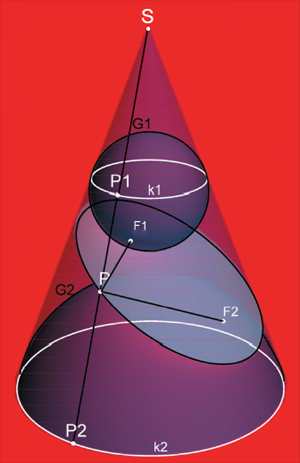
Finally is the hyperbola, the image here courtesy of nabla.hr, which discusses the math succinctly as well — Vladimir Serdarušić at nabla has done a wonderful job on this subject, especially considering how important the images are in understanding the proof. With a hyperbola, the cutting plane intersects both naps of the cone, producing two branches. Now there are two Dandelin spheres, one in each nap. Let \( F_1 \) and \( F_2 \) be their points of tangency with the cutting plane. Let \( P \) be any point on the hyperbola and connect \( P \) to \( F_1 \) and to \( F_2 \). We want to show \( PF_1 - PF_2 \) is constant for all \( P \). Run a straight line up from \( P \) through vertex \( V \), intersecting the spheres at \( N \) and \( M \) respectively. Note that \( PF_1 = PM \), the first being tangent to the upper sphere in the cutting plane, the second tangent to the upper sphere through a line in the cone. Similarly \( PF_2 = PN \), both tangent to the lower sphere. Therefore:

\[ {PF1 - PF_2} = {PM - PN} = MN = \text{ constant}. \]

This follows immediately from the figure, which shows line \( PNVM \) going through vertex \( V \). Circles \( k_1 \) and \( k_2 \), containing points \( M \) and \( N \) respectively, are the intersections of the spheres with the cone, and they are in parallel planes. \( MN \) is just the slant distance between these planes along the angle of the cone. I remember struggling with the hyperbola and still have my picture, much inferior to this one. Amazing how the right image tells the tale, virtually a proof without words.

Mike Bertrand

February 26, 2015

^ 1. Calculus, Volume I, 1^st ed., by Tom Apostol (Blaisdell, 1961).

^ 2. Mémoire sur quelques propriétés remarquables de la focale parabolique (Memoir on some remarkable properties of the focus of the parabola), by Germinal Pierre Dandelin, Nouveaux mémories de l’Académie royale de Bruxelles, 2, 1822, p 171–200.