Archimedes and Pi

Archimedes is one of greatest mathematicians of all time (his name \( A \rho \chi \iota \mu \acute{\eta} \delta \eta \varsigma \) means "master of thought" in Greek). He lived in the third century BC in Syracuse in Sicily (287 BC - 212 BC), then an outpost of Greek civilization. He has been highly regarded since his own time, which is perhaps why much of his work survives. Not all of it though, The Method being turned up in 1906 in the Archimedes Palimpsest (see Wikipedia's write-up as well). What survives is sufficient to measure his stature; he plainly anticipated calculus and knew as well as anyone today what a proof is, heir to the great classical school of Greek mathematics and Euclid. There are a few stories. One is that he was relaxing in his bath pondering the question of whether the king's gold crown had been adulterated and in an instant conceived the notion of buoyancy that bears his name. He was so excited, he jumped up and ran naked through the town shouting "εὕρηκα!" (Eureka - I have found it). It does seem fanciful, but is based on his surviving work On Floating Bodies.
He was a pioneer of physics and engineering as well and is supposed to have invented weapons to keep the investing Romans at bay (the Claw of Archimedes and the heat ray). Archimedes is said to have remarked of the lever, "Give me a place to stand on, and I can move the Earth." They say when the Romans finally came over the walls, he was found in the yard deep in study of some figures in the sand; a Roman soldier stepped forward and cast a shadow on his diagram and Archimedes angrily ordered him away. The soldier slew him on the spot, a perfect metaphor for Roman contempt for theoretical science, practical geniuses that they were.
My source is The Works of Archimedes[1], edited by Sir Thomas Heath, an impressive person in his own right, his prodigious work in classical Greek mathematics being an avocation in an otherwise busy life. Heath included an extensive introduction and modernized the original in various ways, including adding intermediate steps in some cases. I bought my Dover copy in 1970 for $2.00 and it says it's an unabridged reissue of the 1897 edition together with a supplement from 1912. Like all the classical Greek mathematicians, Archimedes work was geometrical through and through. Heath has a section on Archimedes' arithmetic and it is heavy slogging with different Greek letters for tens, hundreds, thousands, and so on; you'd need a higher degree to do long division and it is a small wonder he and his peers could achieve anything whatever involving numerical work. But they did. Heath has a good deal on how Archimedes and his contemporaries probably extracted square roots and in the introduction, asks how in Measurement of a Circle, "Archimedes should all at once, without a word of explanation, give out that":
\[ {1351 \over 780} \gt \sqrt 3 \gt {265 \over 153}. \]
Which amounts to
\[ 1.7320 5128 \gt \sqrt 3 \gt 1.73202614. \]
The higher approximation is within 5 x 10-7, considering that √3 = 1.73205081. Archimedes had a way of teasing readers like that and maybe he gives more away in works now lost, which appear to be extensive; that is exactly what happened in the case of The Method, which turned up early in the 20th century, where Archimedes reveals his physical method for determining areas and volumes - once known, the formulas could be proved. Heath includes The Method, together with helpful introductory remarks. He has a long discussion of how Archimedes may have come up with his approximation of √3 and it is steeped in good mathematics and history. But it seems to me way too coincidental that both these fractions are convergents in the continued fraction expansion of √3 - (1;1,2) in compressed notation and this when expanded:
\[ 1+\cfrac{1}{1+\cfrac{1}{2+\cfrac{1}{1+\cfrac{1}{2+\cfrac{1}{1+\cdots}}}}} \]
The "convergents" of a continued fraction are the fraction taken up to a certain point, leaving off the tail, much like the partial sums of an infinite series. The fourth convergent of the continued fraction above, for example, is:
\[ 1+\cfrac{1}{1+\cfrac{1}{2+\cfrac{1}{1}}} = 7/4. \]
Wolfram Alpha generates the continued fraction above with search term "continued fraction of sqrt(3)" - the default is a closed form if it exists, but click "Fraction form" to get the full blown expression. This very nice continued fraction calculator generates convergents; for the one above (last column is the error, + for over - for under):
| 1 | 1 | 1 | -0.73205081 |
| 2 | 2 | 2 | +0.26794919 |
| 3 | 5 / 3 | 1.66666667 | -0.06538414 |
| 4 | 7 / 4 | 1.75 | +0.01794919 |
| 5 | 19/11 | 1.72727273 | -0.00477808 |
| 6 | 26 / 15 | 1.73333334 | +0.00128253 |
| 7 | 71 / 41 | 1.73170732 | -0.00034349 |
| 8 | 97 / 56 | 1.73214286 | +0.00009205 |
| 9 | 265 / 153 | 1.73202614 | -0.00002466 |
| 10 | 362 / 209 | 1.73205742 | +0.00000661 |
| 11 | 989 / 571 | 1.73204904 | -0.00000177 |
| 12 | 1351 / 780 | 1.73205128 | +0.00000047 |
| 13 | 3691 / 2131 | 1.73205068 | -0.00000013 |
Note Archimedes' approximations as the 9th and 12th convergents, and it's known that such convergents are the best approximations of all fractions with denominators the same or smaller.
But that is a bit of a sideshow. Let's look at the main propositions in Measurement of a Circle, only eight pages, put packed with vital mathematics. Proposition 1 reads:
The area of any circle is equal to a right-angled triangle in which one of the sides about the right angle is equal to the radius, and the other to the circumference, of the circle.
If r is the radius, C the circumference, and A the area of the circle, Archimedes is saying that A = ½r·C. Taken together with proposition 3, where he estimates the ratio of the circumference of a circle to its diameter (π), this is tantamount to the formula A = πr2, probably the most important and best know statement in mathematics after 1 + 1 = 2.
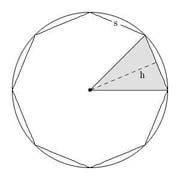 Neither the theorem nor the way it is stated are at all surprising for a Greek mathematician circa 220 BC. That might seem presumptuous and anachronistic, always a danger when trying to evaluate such things from a current standpoint so far in the future. But consider that the Greeks had a highly evolved and sophisticated triangle geometry by the time of Euclid around 300 BC; although The Elements is unquestionably a great work of art that canonized Greek geometry, most of it was discovered before being organized and presented in final form by Euclid. The Greeks liked regular polygons too. In this diagram of an inscribed regular octagon, the area of the gray triangle is ½hs and rotating the triangle around the circle's center repeatedly by 45° fills the octagon with eight congruent copies of that triangle. So the area of the entire polygon is ½h·(s + s + ... + s + s), where there are 8 s's. But there is nothing specific about 8 here - the area of a regular inscribed polygon in general is Area = ½h·Perimeter, and Greek mathematicians had this formula 300 years or more before Archimedes.
Neither the theorem nor the way it is stated are at all surprising for a Greek mathematician circa 220 BC. That might seem presumptuous and anachronistic, always a danger when trying to evaluate such things from a current standpoint so far in the future. But consider that the Greeks had a highly evolved and sophisticated triangle geometry by the time of Euclid around 300 BC; although The Elements is unquestionably a great work of art that canonized Greek geometry, most of it was discovered before being organized and presented in final form by Euclid. The Greeks liked regular polygons too. In this diagram of an inscribed regular octagon, the area of the gray triangle is ½hs and rotating the triangle around the circle's center repeatedly by 45° fills the octagon with eight congruent copies of that triangle. So the area of the entire polygon is ½h·(s + s + ... + s + s), where there are 8 s's. But there is nothing specific about 8 here - the area of a regular inscribed polygon in general is Area = ½h·Perimeter, and Greek mathematicians had this formula 300 years or more before Archimedes.
Even naive intuition tells you that as the number of sides of the polygon increases, h gets closer to the radius and the perimeter gets closer to the circumference, resulting in Proposition 1 in the limit. Anachronism, you say - the Greeks knew nothing of limits. But they did - the method of exhaustion in their terms. That is how Archimedes proved this proposition and the method was developed in earnest 150 years before Archimedes by Eudoxus, basing himself on still earlier work.
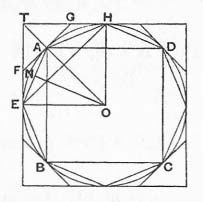
See the sidebar along the top left to show Heath's rendition of Measurement of a Circle in its entirety in a popup window, or examine the work on archive.org. Archimedes' strategy is to start with inscribed and circumscribed squares, then from them inscribe and circumscribe regular octagons, and repeat the doubling process in order to approximate the circle from inside (as suggested above) and outside - the figure here is straight from Heath. Then he assumes in turn that the circle is greater than the triangle or less, and derives a contradiction in each case. It remains that the two must be equal. That is the method of exhaustion and that is his terminology; if A and B are geometric figures, he often says "A is greater than B" rather than "A has greater area than B".
Case 1: He first assumes the circle is greater than the triangle, denoted K (who knows how much Heath has introduced). Let A = Area(Circle) and identify K with ½r·C. Denote the nth inscribed regular polygon as Pn, so P2 is a square, P3 a regular octagon, and so on. Pn+1 is derived from Pn by bisecting the arcs subtended by a side. In other words, Pn is a regular 2n-gon and they are nested and all contained in the circle. Taking the areas for the figures as Archimedes does: P2 < P3 < P4 < ... < A. He says to develop this progression until:
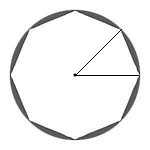
... the sides of the inscribed polygon whose angular points are the points of division subtend segments whose sum is less than the excess of the area of the circle over K.
Archimedes is assuming that the sum of the segments, as pictured in gray here for the octagon, can be made as small as desired by increasing the number of sides of the polygon. It follows that there is a polygon Pm greater than K = ½r·C. But all the polygons are patently less than K:
\[ P_n = \frac{1}{2} h \cdot Perimeter(P_n) < K = \frac{1}{2} r \cdot C, \hspace{10pt} all~n. \]
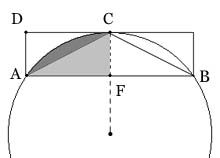
This contradiction proves that the circle cannot be greater than K = ½r·C, which is half the proof. It is true, but not obvious that the sum of the segments goes to zero. To see that it does, consider this diagram, where AB is any chord. If A1 is the dark gray region, then:
\[ \hspace{35pt} A_1 <~\bigtriangleup ADC~=~\bigtriangleup AFC \]
\[ 2 A_1 <~\bigtriangleup AFC + A_1 \]
\[ \hspace{-113pt} A_1 <~{1 \over 2} {(\bigtriangleup AFC + A_1)} \]
But this is the situation when proceeding from Pn to Pn+1. The gray areas taken together, ΔAFC + A1, are one eighth of the excess of the circle over Pn; and A1 is one eighth of the excess of the circle over Pn+1. The expression above shows that the latter is less than half the former. So just as Archimedes says, the sum of the segments can be made as small as desired by increasing the number of sides in the inscribed polygon. Or in modern notation, \( P_n \rightarrow A~as~n \rightarrow \infty \). Which sounds right up to date, but don't be fooled; competent Greek mathematicians of Archimedes' time were familiar with this type of argument and had been for hundreds of years.
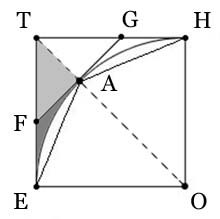
Case 2: Next Archimedes assumes the circle is less than the triangle, and now it's a matter of approximating the circle by a series of circumscribing regular 2n-gons, starting with a square as Q2, an octagon as Q3, and so on like in case 1, but now the polygons are outside the circle. The figure here is suggested by Archimedes and shows the northwest quadrant when progressing from the square to the octagon. In this case, point A is the midpoint of arc EH and FAG is the tangent at A, so \( FAG \perp TAO \). We want to get a handle on how much each polygon exceeds the circle in area. The gray region (both shades together) shows how much the square exceeds the circle, one eighth of it anyway; and the dark gray region shows how much the octagon exceeds the circle, again one eighth.
Archimedes says in essence that ΔEFA < ΔTFA, and that is so because they have the same height and the base of ΔEFA is less than the base of ΔTFA (EF < TF). To see that EF < TF, consider that ΔAOE is isosceles, its angle at O being 45° and its base angles at A and E being 67½°. But ∠OAF and ∠OEF are right angles, so their complements ∠FAE and ∠FEA are equal (22½°). That is, ΔFAE too is isosceles, so EF = FA. But FA < TF in right triangle ΔTFA, so ΔEFA < ΔTFA, QED.
So if A1' is the dark gray region, then:
\[ \hspace{35pt} A_1' <~\bigtriangleup EFA~<~\bigtriangleup FAT \]
\[ 2 A_1' <~\bigtriangleup FAT + A_1' \]
\[ \hspace{16pt} A_1' <~{1 \over 2} {(\bigtriangleup FAT + A_1')} \]
That is, the excess of the octagon Q3 over the circle is less than half of the excess of the square Q2, and similarly the excess of Qn+1 is less than half the excess of Qn. Much like in case 1, we have a series of nested circumscribed polygons Q2 > Q3 > Q4 > ... > A, and where \( Q_n \rightarrow A~as~n \rightarrow \infty \), and we proceed to a contradiction like in case 1: now there must be a polygon Qm' less than K = ½r·C. But all the circumscribing polygons are greater than K:
\[ Q_n = \frac{1}{2} \cdot Perimeter(Q_n) > K = \frac{1}{2} r \cdot C, \hspace{10pt} all~n. \]
This contradiction proves that the circle cannot be less than K, completing case 2..
To recap, case 1 says there is an increasing sequence of inscribed polygons \( P_n \nearrow A \) and assuming K < A
implies there there is an m such that Pm < K < A, leading to a contradiction; therefore K ≥ A.
Case 2 says there is a decreasing sequence of circumscribed polygons \( Q_n \searrow A \) and assuming K > A
implies there there is an m' such that Qm' > K > A, leading to a contradiction; therefore K ≤ A.
Jointly, these force K = A, which is Proposition 1.
Case 1 in Archimedes' proof of Proposition 1 seems particularly abbreviated, considering the exacting requirements of the Euclidean school and indeed of classical Greek mathematics generally. He just asserts that the sum of the segments between the Pn and the circle can be made as small as possible by increasing n. In fact, elements of the proof go back to Eudoxus, if not Hippocrates of Chios, according to Heath in his commentary on Euclid XII, 2:
Circles are to one another as the squares on the diameter.
Note that Eudoxus flourished 150 years before Archimedes, Hippocrates of Chios 200 years before (not Hippocrates the great physician, though they were contemporaries). Euclid proved XII, 2 with the geometric construction and halving argument given in case 1 above. Maybe that's why Archimedes didn't bother to spell it out - it was already well known and no doubt had been for some time before Euclid (E. J. Dijksterhuis[2], a respected authority, says flat out (p 34) that this treatise "is quite evidently a fragment or an excerpt from a longer work" and was in no better shape when Eutocius saw it in the 6th century). Euclid uses a double exhaustion, but each with inscribed polygons in one circle or the other. Archimedes' innovation seems to be adding the circumscribing polygons and exhausting from outside as well as inside. The fact that the area of the circle = ½r·C must have been known to Greek mathematicians long before Archimedes, and Euclid came so close to proving it. You wonder if it had been proven before or maybe Archimedes was the first to give a good argument and just have the nerve to say that constitutes a proof. My suspicion is that Proposition 1 was included for completeness and as prelude to his main result:
Proposition 3 is:
The ratio of the circumference of any circle to its diameter is less than \( 3 {1 \over 7} \) but greater than \( 3 {10 \over 71} \).
I) \( \large{\pi < 3 {1 \over 7}} \). The higher estimate is taken up first and involves the construction of circumscribing regular polygons - hexagon, dodecagon, 24-gon, and so on. The Pythagorean Theorem and Euclid VI, 3 are used repeatedly to get the half side length:
If an angle of a triangle is bisected by a straight line cutting the base, then the segments of the base have the same ratio as the remaining sides of the triangle; and, if segments of the base have the same ratio as the remaining sides of the triangle, then the straight line joining the vertex to the point of section bisects the angle of the triangle.
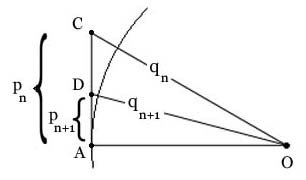
Here is the diagram. Archimedes has O as the center of the circle, OA a radius, and AC tangent to the circle at A, so \(\angle CAO \) is a right angle. He makes \(\angle AOC \) "one-third of a right angle", in other words 30°, so AC is one half the side of a circumscribing hexagon. He wants to get DA, which is one half the side of a circumscribing dodecagon. Simple calculations provide that, since the larger 30°-60°-90° triangle is determined and Euclid VI, 3 gives the ratio in which D cuts AC. The Pythagorean Theorem tells you OD, then you are ready to go again, bisecting \(\angle AOD \), to get the half side of the 24-gon. He continues a couple more times to the 96-gon.
I've added the ps and qs in the diagram to illustrate how to calculate (pn+1, qn+1) from (pn, qn) at each step. We assume the circle has radius 1 (OA = 1) and start with n = 1, where p1 is half the side of the circumscribing hexagon (so p1 = AC = \(\sqrt{3}/3\) and q1 = OC = \(2 \cdot \sqrt{3}/3\)). n doubles at each step - we are dealing with regular 6·2n-gons much as in Proposition 1, though now starting with a hexagon.
Let \( \pi_n \) be twice the perimeter of the nth circumscribed polygon, so (assuming the circle has radius 1), \( \pi_n \) is Archimedes' outside approximation for \( \pi \) at the nth step. Considering that pn is half the side of the nth polygon, \( \pi_n = {{(2 \cdot p_n \cdot 3 \cdot 2^n)} / 2} = {3 \cdot 2^n \cdot p_n} \). So \( \pi_1 \) = \(6 \cdot \sqrt{3}/3\)) = \(2 \cdot \sqrt{3}/3\)) = 3.4641. Proceed as follows to derive (pn+1, qn+1) from (pn, qn):
Euclid says:
\[ {{p_n - p_{n+1}} \over p_{n+1}} = {q_n \over 1}, \]
which, after re-arranging, becomes:
\[ {p_{n+1}} = {p_n \over {q_n + 1}}. \]
Pythagoras says:
\[ {q_{n+1}}^2 = {{p_{n+1}}^2 + 1}, \]
or:
\[ q_{n+1} = {\sqrt{{p_{n+1}}^2 + 1}} \]
Here's the derivation of \( (p_2, q_2) \text{ from } (p_1, q_1) = (\sqrt{3} / 3, 2 \sqrt{3} / 3) \):
\[ \hspace{-54pt} p_2 = {{\sqrt{3} / 3} \over {{2 \sqrt{3} / 3} + 1}} = {\sqrt{3} \over {2 \sqrt{3} + 3}} = {2 - \sqrt{3}} = 0.26795 \]
\[ q_2 = \sqrt{{(2 - \sqrt{3})}^2 + 1} = \sqrt{8 - 4 \sqrt{3}} = {2 \cdot \sqrt{(2 - \sqrt{3})}} = 1.03528 \]
\[ \hspace{-136pt} \pi_2 = {12 \cdot p_2} = 3.21540 \]
The iteration is easy to program in C, a good choice because of reliable IEEE 754 doubles (about 16 decimal digits):
n pi_n error (over)
-------------------------------
6 3.464101615 0.322508962
12 3.215390309 0.073797656
24 3.159659942 0.018067289
48 3.146086215 0.004493562
96 3.142714600 0.001121946
192 3.141873050 0.000280396
384 3.141662747 0.000070093
768 3.141610177 0.000017523
1536 3.141597034 0.000004381
3072 3.141593749 0.000001095
6144 3.141592927 0.000000274
12288 3.141592722 0.000000068
24576 3.141592671 0.000000017
49152 3.141592658 0.000000004
98304 3.141592655 0.000000001
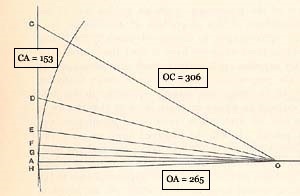
Note the error decreases by better than a factor of four at each step. But let's follow the master. The diagram here is from Heath - it is implicit in Archimedes' text whether in the original or not. The points down the vertical tangent result from bisecting angles at O, D results from bisecting \(\angle AOC \), E from bisecting \(\angle AOD \), and so on. I've added the numbers to highlight Archimedes coordinate system for the proof; note the approximation \(\sqrt 3 = 265 / 153 \) mentioned above. I'm going to use equations rather than inequalities to keep this manageable. Euclid VI, 3 says that
\[ {OC \over OA} = {CD \over DA}. \]
Adding 1 to both sides and noting in the second equality that CD + DA = CA:
\[ {{OC + OA} \over OA} = {{CD + DA} \over DA} = {CA \over DA}. \]
Rearranging gives
\[ \begin{equation}{{OA \over DA} = {{OC + OA} \over CA} = {{306 + 265} \over 153} = {571 \over 153}.} \tag{3} \end{equation} \]
Then from Pythagoras
\[ {OD^2 \over DA^2} = {{OA^2 + DA^2} \over DA^2} = {{571^2 + 153^2} \over 153^2} = {349,450 \over 23,409}, \]
so in an impressive feat of square root taking
\[ \begin{equation}{{OD \over DA} = {{591 {1 \over 8}} \over 153}.} \tag{4} \end{equation} \]
Tying into our ps and qs above, this amounts to:
\[ \hspace{-126pt} p_2 = {DA \over OA} = {153 \over 571} = 0.26795. \]
\[ q_2 = {OD \over OA} = {{OD \over DA} \cdot {DA \over OA}} = {{{591 {1 \over 8}} \over 153} \cdot {153 \over 571}} = {{591 {1 \over 8}} \over 571} = 1.03525, \]
which shows good agreement with the calculations above. Archimedes goes on to calculate the sides of the circumscribed 24, 48, and 96-gon, concluding from the last that:
\[ \pi < {3 {{667 {1 \over 2}} \over {4673 {1 \over 2}}}} = 3.142827 < 3.142857 = {3 {1 \over 7}}. \]
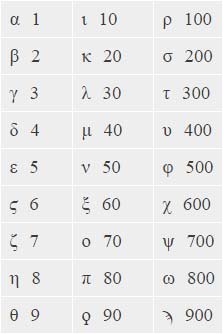
The Greeks of Archimedes' day expressed numbers in a base 10 scheme, but with no zero, one set of letters for units (1 - 9), another for tens (10 - 90), and so on, as shown here. Some gymnastics are required for values over 10,000, a myriad (\(\mu \upsilon \rho \iota \acute{\alpha} \varsigma\)), and fractions use still another notation. Here is the largest value in this section and something like the way Archimedes wrote it:
\[ \Large{{1,373,943 \small{{33 \over 64}}} = \overset{\rho \lambda \zeta}{M}
\unicode{x0375} \gamma \unicode{x03E1} \mu \gamma \unicode{x0384} \hspace{10pt} \lambda \gamma' \hspace{7pt} \xi \delta''}. \]
The capital 'M' signifies myriads and the \( \rho \lambda \zeta \) above it means there are 100 + 30 + 7 = 137 of them. The high and low tick marks around the next four digits mean that part of the number is in the thousands and the first \( \gamma \) stands for 3,000. The three digits after that (\(\unicode{x03E1} \mu \gamma\)) stand for their usual value, namely 900 + 40 + 3 = 943. After the space is the fractional part, the numerator with a single accent and the denominator with a double accent. So the numerator is \(\lambda \gamma\) = 30 + 3 = 33 and the denominator is \(\xi \delta\) = 60 + 4 = 64. It is amazing how far Archimedes pressed this unwieldy numeration system. There is evidence that his great contemporary Apollonius pushed it even harder and refined Archimedes' boundaries for \( \pi \), but no better value is found in the record for another 400 years or so. Liu Hui followed a similar strategy in China and came up with \( \pi \) = 3.1416 by using a 3072-gon in 263 AD. Dirk Struik[3] believes his work was independent of Archimedes, interesting if true because it corroborates how natural this approach is.

II) \( \large{3 {10 \over 71} < \pi} \). Next is to approximate the circle with inscribed regular polygons with 6, 12, 24, 48, and 96 sides in order to bound \( \pi \) from below. Archimedes' setup appears on the right, I can't do better. Note that the angles at C, D, E, and so on are right angles because they are inscribed in a circle and built on the diameter. Start with \(\angle CAB \) = 30°, so BC is the side of an inscribed hexagon. Since AD bisects \( \angle CAB \), BD is the side of a regular dodecagon and Euclid VI, 3 can be applied to to \( \bigtriangleup CAB \). Furthermore, \( \bigtriangleup ACd \sim \bigtriangleup dBD \sim \bigtriangleup ABD \) because all three are right triangles with a second angle the same. The basic idea is to start with BC (side of a hexagon) and AC from the initial 30°-60°-90° triangle; then from these calculate BD (side of a dodecagon) and AD; then iterate the process, running down to E (24-gon), F (48-gon), and G (96-gon). Finally, half the ratio of the perimeter of the 96-gon to AB will be the lower bound for \( \pi \).
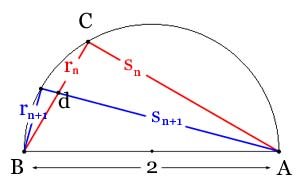
If \(s_0 = AC, r_0 = BC \) (side of the inscribed hexagon), Archimedes in this passage shows how to derive \( s_1, r_1 \) (side of the inscribed dodecagon). I've labeled with \( s_n, r_n, s_{n+1}, r_{n+1} \) in this diagram because the passage to the next step is always the same and Archimedes takes it three more steps with specific calculations like in (3) and (4) above. This is the calculation to get to the next step generally, understanding that the points referenced on the first line will be different at each step:
\[ {s_{n+1} \over r_{n+1}} = {AD \over DB} = \ldots = {{AB + AC} \over BC} = {{2 + s_n} \over r_n} = k_n. \]
Pythagoras says:
\[ s_{n+1}^2 + r_{n+1}^2 = 4. \]
Putting these together:
\[ {{(k_n \cdot r_{n+1})}^2 + r_{n+1}^2} = {r_{n+1}^2 ({k_n^2 + 1})} = 4 ,\]
and therefore:
\[ {r_{n+1} = {2 \over \sqrt{k_n^2 + 1}}}, \hspace{20pt} {s_{n+1} = {k_n \cdot r_{n+1}}}. \]
Here's the derivation of \( (r_2, s_2) \text{ from } (r_1, s_1) = (1, \sqrt{3}) \):
\[ r_2 = {2 \over \sqrt{{(2 + \sqrt{3})}^2 + 1}} = {1 \over \sqrt{2 + \sqrt{3}}} = 0.51764 \]
\[ \hspace{-34pt} s_2 = {{2 + \sqrt{3}} \over {\sqrt{{2 + \sqrt{3}}}}} = {\sqrt{{2 + \sqrt{3}}}} = 1.93185 \]
\[ \hspace{-101pt} \pi_2' = {6 \cdot r_2} = 3.10583 \]
That's for the dodecagon. Archimedes does this calculation, and carries it forward for the 24-gon, 48-gon, and 96-gon. He finally comes up for this for the 96-gon:
\[ \pi > {3 {{6336 \over {2017 {1 \over 4}}}}} = 3.14091 > 3.14085 = {3 {10 \over 71}}, \]
Below is the output from the C program based on the r's and s's. Note the values for the dodecagon and 96-gon agree reasonably with the foregoing, considering the dependence on an approximation for \( \sqrt{3} \); also that the error decreases by a little more than a factor of four at each step:
n pi_n' error (under)
-------------------------------
6 3.000000000 0.141592654
12 3.105828541 0.035764112
24 3.132628613 0.008964040
48 3.139350203 0.002242451
96 3.141031951 0.000560703
192 3.141452472 0.000140181
384 3.141557608 0.000035046
768 3.141583892 0.000008761
1536 3.141590463 0.000002190
3072 3.141592106 0.000000548
6144 3.141592517 0.000000137
12288 3.141592619 0.000000034
24576 3.141592645 0.000000009
49152 3.141592651 0.000000002
98304 3.141592653 0.000000001
To recap the approximation of \( \pi \):
\[ 3.14085 < \pi < 3.14283. \]
Averaging the two bounds, \( \pi \approx 3.14184 \), an error of \( 2.6 \times 10^{-4} \) or about one part in 4,000. Pretty good with the tools at hand and the record for some 400 years, at least in any surviving document. This method continued to be used for over 1,800 years to squeeze out more and more digits for \( \pi \) and appeared in different parts of the world until being replaced in the 17th century by infinite series. According to Plutarch, it was one of Archimedes' great talents to prove what no one else could and do it in such a smooth and clear way that after the fact, everyone says, well of course.
With the possible exception of Heath, the best single best source for studying the mathematics of Archimedes in English (or Dutch) is Dijksterhuis' Archimedes, listed at the bottom. After fifty pages of well-informed preliminaries, he includes all or almost all of the mathematical treatises, following Archimedes closely, but not being shy to include modern commentary in modern notation, much as I've attempted above. When discussing The Measurement of a Circle, he includes Archimedes' Greek numerals for ratios right next to the way we write them. This book was originally published in English in 1956 and was reissued in paperback by Princeton University Press in 1987; it is now sadly out of print.
Marshall Clagett starts his monumental Archimedes in the Middle Ages[4] like this:
The importance of the role played by Archimedes in the history of science can scarcely be exagerated. He was emulated and admired in his own day and at successive periods in later times. His name appears on the pages of the works of the great figures who fashioned the beginnings of modern mechanics. For example, Galileo owed a not inconsiderable debt to Archimedes - both direct and indirect. Galileo mentions Archimedes by actual count over one hundred times and in almost Homeric hyperbole, using such expressions as suprahumanus Archimedes, Archimedes inimitabilis, divinissimus Archimedes, and so on. Archimedes' significance for these founders of early modern science lay in the use of mathematics in the treatment of physical problems as well as in the originality and fertility of his mathematical techniques. But all of this is well known.
Clagett goes on to recount Archimedes' signal importance in the early middle ages. Plutarch's classic account of Archimedes in the Life of Marcellus gave weight to the legend (Plutarch was a Roman citizen of Greek extraction who wrote in Greek - dates 46 AD - 120 AD). In defending his home town Syracuse, Archimedes is shown unleashing a veritable Godzilla, terrifying the poor Romans with awesome engines of war that plucked entire ships from the water, to be shaken mercilessly and tossed aside like pebbles. The account continues for nine pages, biblical in scope and with a similar effect down through the ages. Few if any of even the foremost scholars of Latin Christendom before 1,100 AD had or could read classical Greek texts; nor did they have access to Latin translations, but hints of the great one leaked out to them, revered as a magus at first and increasingly as a great engineer, scientist and mathematician.
There was an early renaissance in the 12th century ("renaissance" signifying rebirth and entailing connection with and recovery of classical learning). Scholars went to border regions to learn Arabic, there to locate the Greek classics in Arabic translation and translate them in turn to Latin, accessible to all scholars in the Christian lands. Clagett (p 30) ascribes the first good and popular Latin translation of Measurement of a Circle to the celebrated Italian translator Gerard of Cremona, a diligent worker circa 1150-1187 in Toledo, then a cosmopolitan center and maintained as such by Moors and Castilians alike as the city changed hands. Here is the beginning of Gerard's translation, next to Clagett's English translation of that (Claggett, pp 40-41):
So an English translation of a Latin translation of an Arabic translation of the original Greek, intervening Syriac or Persian versions quite possible between the last two. Even the term "original Greek" is in question, Dijksterhuis (p 35-36) saying that the 6th century Byzantine mathematicians Eutocius and Isidore of Miletus and their school translated this work into then current Attic from Archimedes' classic Siculo-Dorian dialect (others think that transition occurred even earlier). Keep in mind that Eutocius and Isidore were further removed from Archimedes in time than we are from Chaucer. And that works could degrade rapidly, necessitating constant copying over time. The wonder is not that some of Archimedes' original manuscript is lost, but rather that any of it remains remotely intact.
Heath says in the preface:
My main object has been to present a perfectly faithful reproduction of the treatises as they have come down to us, neither adding anything nor leaving out anything essential or important. The notes are for the most part intended to throw light on particular points in the text or to supply proofs of propositions assumed by Archimedes as known; sometimes I have thought it right to insert within square brackets after certain propositions, and in the same type, notes designed to bring out the exact significance of those propositions.

The first translation from the Greek in the West is due to the Flemish Dominican William of Moerbeke in 1269, the start of a long tradition. William's Latin translation, in his own hand, is still in the Vatican library. The foremost modern translator from the Greek is the great Danish classical philologist Johan Ludvig Heiberg (1854-1928). Heath got the Greek from Heiberg's 1880 edition of the complete works[5] (immense pdf), the canonical source till this day (Heiberg included his own Latin translation on opposing pages, left-click the link to see it in a popup window). Discussing the provenance, Heath continues:
The MSS. of the best class all had a common origin in a MS. which, so far as is known, is no longer extant. It is described in one of the copies made from it ... as 'most ancient' (\(\pi \alpha \lambda \alpha \iota \omicron \tau \acute{\alpha} \tau \omicron \upsilon\)), and all the evidence goes to show that it was written as early as the 9th or 10th century.
There's a good chance this ancestral manuscript (Heiberg's Codex A) is in turn based on copies of Isadore and Eutocius. This manuscript, itself now lost, included the commentaries of Eutocius and you can see his addenda inlined in Heiberg's edition (left-click for popup window).

Early in the 20th century, Heiberg was alerted to the existence of an old Greek manuscript in the possession of the Greek Orthodox Church in Constantinople with suspicious mathematical writing underneath its religious exterior. This was a common practice in days past, valuable parchment being reclaimed by monks, scrubbed of its original unwanted text to take the new. Heiberg went to Constantinople in 1906 to examine the palimpsest (for that is what such a recycled document is called). He could actually read much of the writing underneath and determined immediately that it was an old Archimedes codex (ancient manuscript in book form). Not allowed to remove it, he had quality photographs taken for further study back in Copenhagen. He deciphered most of it, which contained many of the known works, a copy of On Floating Bodies not in Codex A, and a new work called The Method (\(E \phi \omicron \delta \omicron \varsigma \)), mentioned by ancient authors but not previously extant. Archimedes showed there how to physically find the center of gravity and volume of solid figures, anticipating both modern mechanics and calculus. Heiberg incorporated all this into a new edition of Archimedes' works published between 1910 and 1915. It was an explosive find, a Greek Archimedes going back to 975 AD or so, hundreds of years earlier than anything else extant and including the previously lost and immensely important Method (nice Wikipedia writeup here). He denoted the new work Codex C.
Stunningly, the codex fell from sight for most of the 20th century, badly used by criminals and vandals, marred by petty forgers and allowed to mold away in a fashion more destructive than anything the monks had done. Ironically, the old overwrite from the 13th century had served to preserve the codex both physically and socially, making it something generations of monks valued and wanted to retain. By a circuitous route, the palimpsest came to sale at Christie's in 1998 and was sold to a "high tech American", who (finally!) lent it to scholars and technical workers for preservation, copying, and study, even financially supporting the effort. Digital techniques and ultraviolet photography are now being employed to show every last letter in the Archimedian text.
The tale is told by two of the modern principals, historian of mathematics Reviel Netz and curator Will Noel in The Archimedes Codex[6]. It's a tossup whether Netz's mathematics or Noel's historical detective work and modern technology is more interesting - see Professor Berggren's informative and balanced review here. The codex was originally written around 975 AD based on earlier copies and copied over by a scribe whose name was Ioannes (John) Myronas in 1229 AD. Netz hazards that "scribes, typesetters, and publishers make a silent contribution to the history of science, sometimes as important as that of the scientists themselves", remarking pregnantly that the abbreviations they introduced to render Archimedes are a form of mathematical notation similar in kind to modern notations. In the end, Heiberg got most of the text on summer vacations in Constantinople in 1906 and 1908, aided by his photographs and a magnifying glass.
Professor Alexander Jones' review of Netz's translation of Archimedes' On the Sphere and the Cylinder published in Notices of the AMS (52:5) is a particularly lucid and compact account of much of the foregoing. The professor is well-versed on all the subjects in play, being an expert of ancient Greek science and its transmission to succeeding generations.
Scholars for 2,200 years have lost sleep carefully copying, storing, translating, emending, and transmitting these and other such works, the deepest heritage of the human race. Remember, no printing for most of this time! Countless anonymous Hellenic, Byzantine, Islamic and Christian scribes and others labored away over the centuries, in many cases hardly understanding what they were copying, driven by the faint but increasingly audible echo of past greatness. Also by the thought that intellectual pursuits too served the Lord, an idea gaining momentum in the West in the 12th century and reaching an apotheosis soon after in the immensely influential Thomas Aquinas (1225-1274).
What a privilege to read and comment on it all these years later (itself a grand tradition) and see how very modern, how very right it is, mathematically speaking. It's as if a whisper from the great ancient one, the Master of Thought, once almost silenced, has gained enough strength down through the ages to waken us from our slumbers.
Mike Bertrand
May 16, 2014
^ 1. The Works of Archimedes, with the Method of Archimedes, by T. L. Heath (ed.), Dover (1912, reissue of the 1897 edition with supplement on The Method), ISBN 978-0486420844 (2002 ed.).
^ 2. Archimedes, by E. J. Dijksterhuis, Ejnar Munksgaard, Copenhagen (1956), ISBN 978-0691024004 (1987 ed.).
^ 3. A Concise History of Mathematics (4th Revised Edition), by Dirk J. Struik, Dover (1st ed. 1948, 4th ed. 1987), ISBN 978-0-486-60255-4. See p 73 for Liu Hui.
^ 4. Archimedes in the Middle Ages, Vol. I: The Arabo-Latin Tradition, by Marshall Clagett, The University of Wisconsin Press, Madison (1964).
^ 5. Archimedis Opera Omnia cum Commentariis Eutocii (link to Vol I, immense pdf), by Johan Ludvig Heiberg, Teubner, Leipzig (1880).
^ 6. The Archimedes Codex, by Reviel Netz and William Noel, Phoenix / Orion Books, Ltd. (2008), ISBN 978-0-7538-2372-9. "originally written around 975 AD": p 84; "Ioannes (John) Myronas in 1229 AD: pp 274-5, p 227; "silent contribution": p 109.
