Resurrecting Tartaglia
Niccolò Tartaglia (1499-1557) was badly used by Cardano and his disciples and has been deprecated ever since, as if to prove the old adage about hating those the most whom you've unjustly injured the most. His partial solution of the cubic equation, expropriated by Cardano, should have propelled him into the first rank of mathematicians of his day[1]. Instead, it's been used to run him down, the supposedly small-minded foil to the great Cardano. In fact, the impoverished, self-trained Tartaglia was highly productive and exemplified the forward-looking mathematizing approach to the new science leading in direct line to Galileo and the modern approach generally.[2] First and foremost, Tartaglia was a maestro d'abaco, that is, a teacher of the new art of calculation with pen and paper. This tradition centered in vernacular commercial schools outside the universities, sidestepping the barren Boethian preoccupations of "mathematicians" debating endlessly in Latin quaestios about such matters as the true nature of even and odd numbers and what that might mean for the cosmos.
These schools are sometimes called "abacus schools" in English, but it was not the abacus they taught, but rather the kind of calculation practiced today by every grade-schooler. Not abstract calculation either, but calculations geared towards practical problems like currency exchange, surveying, and book-keeping. Problem solving was one of the main pedagogical approaches, a point-of-contact with the Tartaglia-Cadano controversy. Algebra too, insofar as it was necessary to solve problems. This was before anything like the liberating modern notation, of course, but they felt their way, the unknown \( x \) being the cosa (the thing) — hence the term cossists for practitioners of this art. The rechenmeisters in Germany were in the same vein, Adam Ries being a leading practitioner there.
Lucien Febvre writes of the "quest for knowledge" among plebeians as well as the better-off in renaissance France, including the amazing Thomas Platter (1499-1582), who with a heroic effort "tried to clear the heavy layer of cobwebs from his brain [and] carried on single combat with the Latin grammar of Donatus". Serving his masters by day, he studied alone at night, "fighting sleep by putting cold water or raw turnips or pebbles in his mouth to put his teeth on edge so that he would wake immediately should he doze off", thereby teaching himself Greek and the rudiments of Hebrew as well as Latin.[3] Tartaglia, born the same year, was like that:
The surname Tartaglia, which Niccolò always used, was a nickname given to him in his boyhood because of a speech impediment resulting from a wound in the mouth (tartagliare means “to stammer”). ... Tartaglia’s father, Michele, a postal courier, died about 1506, leaving his widow and children in poverty. Six years later, during the sack of Brescia, Niccolò, while taking shelter in the cathedral, received five serious head wounds. It was only through the loving care of his mother that he recovered. At the age of about fourteen, he went to a Master Francesco to learn to write the alphabet; but by the time he reached “k,” he was no longer able to pay the teacher. “From that day,” he later wrote in a moving autobiographical sketch, “I never returned to a tutor, but continued to labor by myself over the works of dead men, accompanied only by the daughter of poverty that is called industry” (Quesiti, bk. VI, question 8).[4]
I might add that this "sack of Brescia" in 1512 resulted in the brutal murder of some 45,000 defenseless men, women, and children there over five days by a crazed and uncontrolled French army, their commander angry because the Brescians had dared to defy him. It appears that Brescia never recovered from this atrocity. Tartaglia moved to Verona around 1517, then to Venice in 1534, a major European commercial hub and one of the great centers of the Italian renaissance at this time.
Working class mathematician — that is exactly the phrase Mario Biagioli uses for Tartaglia[5], and it is triply apt. He was dirt poor throughout life and died penniless despite lasting contributions only dreamed of by many of his his "betters". One of those was Cardano, by the way, an upper class professor of medicine who showed nothing but contempt for Tartaglia even as he robbed him. Tartaglia tried to improve himself materially and socially through his abbaco practice; he eked out a living teaching practical mathematics in abbaco schools and earned a penny where he could:
This remarkable man [Tartaglia] was a self educated mathematics teacher who sold mathematical advice to gunners and architects, ten pennies one question, and had to litigate with his customers when they gave him a worn out cloak for his lectures on Euclid instead of the payment agreed on.[6]
Practical applications, that was the key interest of the abbaco tradition. He hoped to attract a patron with his work on the cubic as well as his ballistics — that was one of the few paths to self-improvement for someone like him. Patronage was a major driving force of the new science in those days. We would know nothing of Copernicus were it not for his enabling bishop. Or consider the case of Galileo two generations later, someone who cultivated potential patrons assiduously and had to if he were to proceed.[7]
Nova scientia (1537) was Tartaglia's first published work, described by Matteo Valleriani as:
... one of the most fundamental works on mechanics of the Renaissance, indeed, the first to transform aspects of practical knowledge accumulated by the early modern artillerists into a theoretical and mathematical framework.[8]
Reverence for Aristotle had hobbled progress in physics. The problem was that Aristotle had a physics, and a thoughtful one for its day, but treated by the schoolmen like scripture 1800 years after being set down. Artillery and projectile motion posed problems that Aristotelian categories like "heavy" and "natural" and "violent" motion could not helpfully address. Recall too that this was the period of the Italian wars, when Venice and northern Italy were struggling for survival and looking to military art to save themselves. Mary J. Henninger-Voss writes that "Tartaglia's dynamics eviscerated Aristotelian terms of projectile movement".[9] Aristotle liked to focus on causes, what we would call force today, and its study, dynamics. But he banned mathematics from physics. Tartaglia brought it back in and focused mainly on where that cannonball was going to go — that is, kinematics, the science of the motion itself. That is exactly what one would expect from a practical mathematician, one trying to profit from his work and to find a patron.
Tartaglia's approach was decidedly mathematical. One of his findings was that the maximum range of a projectile was achieved by directing the cannon at a 45° angle to the horizon (I still remember the joy of proving that as a young physics student all those years ago). The proof had to wait for Galileo, who was also highly interested in this subject, but still. Tartaglia wasn't fully emancipated from an Aristotelian approach or from his idol Euclid. Henninger-Voss emphasizes this aspect of Tartaglia or of any transitional figure really, how categories are blurred and confused, how rigor is replaced by eclectic thinking driving for results. Of course he recognized that the trajectory was curved, but he patched together circular and rectilinear motion to get the curve. Tartaglia knew of Archimedes' work on the quadrature of the parabola from Guarico's Latin edition of 1503, which he had found "in the hands of a sausage-seller in Verona in 1531" (in mano di un salzizaro in Verona, l'anno 1531), but deeper understanding of the conic sections was wanting in Europe at that time; consider that Apollonius's great work on the conic sections was not published until 1566.
But that bears discussion too. Just because Apollonius was published in a book somewhere in Europe in 1566 does not mean that a poor scholar in Venice had immediate access to it. All the same, Venice was the printing cockpit of Europe at this point, the biggest publishing center in the world, and Tartaglia did have the advantage of association with wealthy scholars and book collectors, including churchmen, who provided him access to expensive and sometimes rare manuscripts and books. In that respect, he was in the right place at the right time.
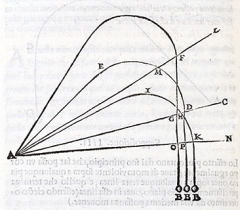
Tartaglia's model for a cannonball's flight was that it proceeded from the cannon in a straight line, then after a while started to arc towards the earth along a circular path, then finally dropped in another straight line directly towards the earth — examine the image above to get a sense of this for different elevations of the gun. At the end of Book 2 of Nova scientia, Tartaglia proposes to find the length of that initial rectilinear path for a projectile fired at an elevation of 45°[10]. He writes that Archimedean methods showed that the horizontal range in such a case was ten units, assuming that the initial rectilinear path for a projectile fired point blank (that is, at 0°, or parallel to the ground) is one unit. Presumably "Archimedean methods" meant experiment or practical data of some kind.
Here is the diagram, where the cannon is at point \( A \) and shoots a projectile at \( \angle EAH = 45^{\circ}. \) Also, \( AI = 10. \) The task is to find \( AH. \) Tartaglia painstakingly constructs the diagram shown here, appealing repeatedly to propositions from Euclid. In order to conclude that the area of \( \bigtriangleup \! ALO \) is \( 100, \) for example, he cites:
Euclid Book I, Propostion 41
If a parallelogram have the same base with a triangle and be in the same parallels, the parallelogram is double the triangle.
He first constructs the parallel lines \( CD \) and \( LK \) perpendicular to \( AI, \) having located points \( L \) and \( O \) so that \( \bigtriangleup \! AIL \) and \( \bigtriangleup \! AIO \) are congruent isosceles right triangles and \( AI \perp LO. \) So there is an implicit rectangle between the parallels with width \( AI = 10 \) and length \( LO = LI + IO = 10 + 10 = 20. \) The rectangle has area \( 200 \) and so \( \bigtriangleup \! ALO, \) which is between the parallels and has the same base as the rectangle, has half its area, namely, \( 100. \)
He proceeds by calculating the area of \( \bigtriangleup \! ALO \) in a different way and then solving for an unknown. Letting \( x = AH = HP = \text{radius of the circle}, \) we note that \( \bigtriangleup \! ALO = \; \bigtriangleup \! ALP \; + \bigtriangleup \! LOP \;+ \bigtriangleup \! OAP, \) where the altitude of each one of those three component triangles is \( x. \) Using the formula for the area of a triangle that area = ½ ∙ base ∙ height for each of those component triangles gives another expression for this area:
\begin{align}
\text{Area}(\bigtriangleup \! ALO) &= \text{Area}(\bigtriangleup \! ALP) + \text{Area}(\bigtriangleup \! LOP) + \text{Area}(\bigtriangleup \! OAP)\\
&= {{1 \over 2} \cdot AL \cdot x} + {{1 \over 2} \cdot LO \cdot x} + {{1 \over 2} \cdot OA \cdot x}\\
&= {x \over 2} \cdot (AL + LO + OA)\\
&= {x \over 2} \cdot (10 \sqrt{2} + 20 + 10 \sqrt{2})\\
&= {20 x \over 2} \cdot (\sqrt{2} + 1)\\
&= 10 x \cdot (\sqrt{2} + 1).\\
\end{align}
Equating the two expression for the area of \( \bigtriangleup \! ALO \) and solving for \( x \) results in:
\begin{align}
x &= {10 \over {\sqrt{2} + 1}}\\
&= 10 \cdot {{\sqrt{2} - 1} \over {({\sqrt{2} + 1}}) ({\sqrt{2} - 1})}\\
&= 10 \cdot {{\sqrt{2} - 1} \over {2 - 1}}\\
&= 10 \cdot (\sqrt{2} - 1)\\
&= 4.14\\
&\sim 4 {1 \over 7}.\\
\end{align}
This is exactly Tartaglia's argument, though he doesn't have modern notation or use \( x \) for the unknown. He writes as follows, the original in the Venetian dialect as it usually was for him:
Hor uolendo saper per numero la quantita della retta AH primamente del centro P duceremo le due linee PL et PO procederemo per algebra, pomendo che il semidiametro del cerchio sia una cosa.
Now, if we want to know the measurement of the straight line AH by means of numbers, we first of all produce two lines PL and PO from the center P and then proceed algebraically. We assume that the semidiameter of the circle is one cosa.[11]
The cosa is \( x \)! There are a number of striking aspects to this demonstration. Note the construction of what amounts to a coordinate system with perpendicular \( x \) and \( y \) axes, this exactly one hundred years before Descartes' La Géométrie in 1637. Also the association of numbers with geometric objects and a readiness to measure line segments and areas indiscriminately with the same unit (line segments and areas are inherently different and can't be mixed like this in a strictly Euclidean tradition). Bringing in algebra, with the cosa standing for a line segment no less, introduces a radically new approach. And all in the service of modelling a physics problem in a way antithetical to Aristotelian thought, which still dominated polite university discourse.
Mary J. Henninger-Voss notes that "Tartaglia's work on military science had an enormous circulation throughout Europe", being a reference for common gunners into the eighteenth century, sometimes through unattributed translations. He influenced Galileo as well, who owned "richly annotated" copies of his works on ballistics as he set about solving the projectile problem once and for all.[12]
The first task of scientists in this period was to break the death grip of the logic-chopping universities. By the time a young scholar learned the necessary Latin, he too was in thrall to the barren scholasticism practiced there, closing the loop. Tartaglia's lack of education was oddly liberating, his independence, drive, and practical bent more than compensating for formal training.
The new science associated itself with Archimedes, at first simply from the atavistic intuition that in antiquity it was he who harnessed mathematics in the defense of Syracuse from the Roman invaders in 212 BC. Archimedes' works were first available in Europe in the twelfth century in Latin translations from the Arabic and included pure mathematics like the quadrature of the circle and parabola, but also works of mathematical physics in hydraulics and and statics (finding the center of gravity, for example). His manuscripts were few and badly understood in the age of bowdlerized Euclid and the reigning scholastic tradition[13], but they began to be studied outside the universities in Tartaglia's day as exemplary of the notion that mathematics is the key to understanding physics. The great translator and mathematician Federigo Commandino only reflected his peers when saying in 1558 that "with respect to geometry no one of sound mind could deny that Archimedes was some god" and that:
It has always been my opinion that a mathematician who has not studied the works of Archimedes accurately ought scarcely to be called a mathematician. For such a mathematician [who does not know Archimedes] would be harassed by an ignorance of many things without which mathematical disciplines would have to be, in a certain way, imperfect and inchoate."[14]
All the more credit for Tartaglia, who published a Latin edition of Archimedes in 1543, Opera Archimedis Syracusani philosophi et mathematici ingeniosissimi, which included the following (the first titles are Tartaglia's, the parenthesized ones the titles in T. L. Heath's English translations):
- De Centris Gravium / On the Centers of Gravity (On the Equilibrium of Planes), Book I
- De Centris Gravium / On the Centers of Gravity (On the Equilibrium of Planes), Book II
- Quadratura Parabola / Quadrature of the Parabola (Quadrature of the Parabola)
- (No title) / Measurement of the Circle (Measurement of the Circle)
- De Insidentibus Aquae / On Bodies in Water (On Floating Bodies), Book I
Opera Archimedis is 71 pages long and is full of inline diagrams, the preparation of which was no mean task in those days. Tartaglia was working from a manuscript copy of Moerbeke's thirteenth century Latin translation from the Greek, not that he knew it (Moerbeke didn't sign his original Archimedes manuscript and its provenance wasn't nailed down until the Marshall Clagett's pioneering work in the 1970s).[15] Most of the text is Moerbeke's, but Tartaglia added some interpolations. The Circle and Parabola were published by Gaurico in 1503, whose work was likely consulted by Tartaglia; the others had not been printed previously and were based on a manuscript copy or copies. Tartaglia published Italian versions of some Archimedean texts later in life, his executor continuing to publish his translations after his death.

Disseminating good editions of Euclid also occupied Tartaglia, another critical task for humanist mathematics in this period. He translated Euclid into Italian from Latin and published the work as Euclide Megarense philosopho, also in 1543. This was the first published edition of Euclid in any vernacular language, German, French, and English translations following some twenty years later.[16] This work went through many editions in the sixteenth century and helped diffuse knowledge of mathematics to a non-academic but increasingly well-informed literate public in Italy.
Euclid had been available in manuscript in Europe since Adelard of Bath's translation from Arabic to Latin in the twelfth century — available but dimly understood in a scholastic tradition foreign to exacting Euclidean logic. Antoni Malet describes Tartaglia's Euclid as "mathematically cogent, innovative, and influential", noting that he modified the text available to him with happy results, correcting medieval manuscripts regarding the pivotal topic of proportion.[17] Let Mary J. Henninger-Voss have the final word on Tartaglia the translator and publisher:
Because Tartaglia was the "rude mechanic" of mathematicians, he was seldom highly celebrated by his high-brow colleagues. His own student, Giovan Battista Benedetti cited him to refute him, and Cardano and Ferrari dismissed him as a teacher of little boys. Nevertheless, Tartaglia was a mathematical force to reckon with, if only because he out-sold most other mathematicians of his century. He both attracted readers to his new science, and made widely available editions of Euclid in Italian, and Archimedes in Latin and Italian. It is probably through the editions of Tartaglia that Galileo first learned the work of the "divine Archimedes."[18]
The Republic of Venice was a commercial and political powerhouse in the sixteenth century, a maritime empire with outposts as far away as the Black Sea, and increasingly a cultural center driven by the printing press. The first printed arithmetic was published at Treviso in 1478, today a suburb of Venice and incorporated into the Republic in 1339.[19]
Such printed abacco books became common, written typically by maestros d'abaco and used in their extensive network of commercial schools. This business civilization spawned Niccolò Tartaglia and he rose to the occasion with the General Trattato di Numeri et Misure (General Treatise on Number and Measure)[20], a 1500 page encyclopedia in six parts written in the Venetian dialect, the first three coming out in 1557 about the time of Tartaglia's death and the last three published posthumously by his literary executor and publisher Curtio Troiano in 1560. David Eugene Smith wrote of the General Trattato that it was:
the best treatise on arithmetic that appeared in Italy in his century, containing a very full discussion of the numerical operations and the commercial rules of the Italian arithmeticians. The life of the people, the customs of the merchants, and the efforts at improving arithmetic in the 16th century are all set forth in this remarkable work.[21]
Part I is 554 pages long and constitutes essentially a commercial arithmetic, taking up such topics as basic operations with the complex currencies of the day (ducats, soldi, pizolli, and so on), exchanging currencies, calculating interest, and dividing profits in joint companies. The book is replete with worked examples with much emphasis on methods and rules (that is, algorithms), all ready to use virtually as is. Tartaglia served Venice with this work, and others too as it became translated in following years (into French, by Gosselin, for example). Served Venice, but exemplified it as well with his entrepreneurial spirit. Just looking at Part I, what an impressive artifact, with beautiful block plate leading letters, inset tables, and a dizzying array of symbols for all those currencies. Here's a example from Book 3, showing how to add up a series of values in the mixed Venetian currency of the day:
The circled symbols denote units of Venetian currency: ducats, lire, soldi, and pizzoli. Tartaglia notes that 12 pizzoli make a soldo (che pizzoli 12 fanno un soldo), 20 soldi make a lira, and 6 lira and 4 soldi make a ducat — this last causes some difficulties. Let's walk through the calculation, starting with the pizzoli in the right column. They add up to 10 + 9 + 8 + 6 + 7 = 40 pizzoli = (3 x 12 + 4) pizzoli = 3 soldi + 4 pizzoli. Write 4 at the bottom of the pizzoli column and carry the 3 soldi to the next column to the left. Next add up the soldi, including the carried 3 carried ones: 3 + 13 + 12 + 4 + 10 + 19 soldi = 61 soldi = (3 x 20 + 1) soldi = 3 lire + 1 soldo. Write 1 at the bottom of the soldi column and carry the 3 lire. Then add up the lire, including the 3 carried ones: 3 + 3 + 4 + 5 + 3 = 18 lire. Write 18 at the bottom of the lire column. Finally add up the ducats: 754 + 375 + 569 + 37 + 5 = 1740 ducats. Write 1740 at the bottom of the ducats column. So the provisional sum is 1740D : 18L : 1S : 4P, where (D, L, S, P) stand for (ducats, lire, soldi, and pizzoli) respectively.
We need an adjustment to the 18 lire, which amounts to 2 ducats and then some. A ducat is 6 lire and 4 soldi, so 2 ducats equals 12 lire and 8 soldi. Add the two ducats to that column, now totaling 1742 ducats. Then subtract those two ducats (in the form of 12 lire and 8 soldi) from the previously calculated values for lire and soldi, namely, 18 lire and 1 soldi. That is, execute the calculation (18L : 1S) - (12L : 8S) = (5L : 13S), after borrowing. The pizolli are unaffected but there are new values for the lire and soldi. As Tartaglia shows, the final sum is (1742D : 5L : 13S : 4P).
This is but one example and a simple one. Varied commercial calculations continue for hundreds of pages and it took a prodigious amount of work not only to prepare the manuscript, but to typeset the book — Tartaglia must have lived at his printer's.
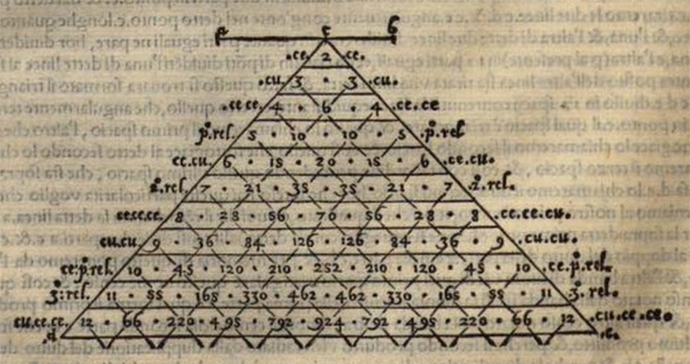
Part II takes up more general arithmetic problems, including progressions, powers, binomial expansions, Tartaglia's Triangle (as "Pascal's Triangle" is still called in Italy), calculations with roots, and proportions / fractions. Consider this from Book 2:
The numbers on the right are given as eight products (primo produtto through ottauo produtto). The tip-off is the eighth product \( 16384 = 2^{14} = 4^7 \), that together with the fact that the sum at the bottom (summa) is \( 10000000 = 10^7 \). Powers of \( 2 \) are listed elsewhere in the book if there is any question about that. In fact these are the summands in the binomial expansion:
\begin{align}
10^7 &= (6+4)^7\\
&= {7 \choose 0} \cdot 6^7 + {7 \choose 1} \cdot 6^6 \cdot 4 + {7 \choose 2} \cdot 6^5 \cdot 4^2 + \cdots + {7 \choose 5} \cdot 6^2 \cdot 4^5 + {7 \choose 6} \cdot 6 \cdot 4^6 + {7 \choose 7} \cdot 4^7\\
&= \color{red}{1} \cdot 6^7 + \color{red}{7} \cdot 6^6 \cdot 4 + \color{red}{21} \cdot 6^5 \cdot 4^2 + \color{red}{35} \cdot 6^4 \cdot 4^3 + \color{red}{35} \cdot 6^3 \cdot 4^4 + \color{red}{21} \cdot 6^2 \cdot 4^5 + \color{red}{7} \cdot 6 \cdot 4^6 + \color{red}{1} \cdot 4^7\\
&= 279,936 + 1,306,368 + 2,612,736 + 2,903,040 + 1,935,360 + \color{blue}{21 \cdot 36 \cdot 1024} + 172,032 + 16,384
\end{align}
The red numbers in the third line are the binomial coefficients. The blue product on the last line is the sixth product when multiplied out (sesto produtto): \( \color{blue}{21 \cdot 36 \cdot 1024 = 774,144}. \) You can make out in Tartaglia's highlighted text how the \( 21 \) is multiplied by \( 1024 \) to make \( 21504 \) and then that is multiplied by \( 36 \) to make \( 774,144. \) I have to admit to making a number of mistakes when following this calculation, calculator in hand. That Tartaglia, his publisher, and their helpers filled hundreds of pages like this with precise and correct calculations (if my spot checks are any indication) testifies to their mathematical acuity and the high production values they brought to making this book.
It won't be a surprise at this point that Tartaglia knew of "Pascal's Triangle" one hundred years before Pascal, as shown in this extract from the General Trattato:
His examples are numeric, but he thinks about it geometrically, the horizontal line \( ab \) at the top of the triangle being broken into two segments \( ac \) and \( cb, \) where point \( c \) is the apex of the triangle. Binomial expansions amount to taking \( (ac + cb)^n, \) for exponents \( n = 2, 3, 4, \cdots \) as you go down the triangle. The symbols along the outside represent powers at this early stage of algebraic notation: \( ce = 2, cu = 3, ce . ce = 4, \) and so on. He writes explicitly about the additive formation rule, that (for example) the adjacent \( 15 \) and \( 20 \) in the fifth row add up to \( 35, \) which appears beneath them in the sixth row.
Here he explains how to cube a binomial and fill out the second row of the triangle accordingly, writing:
che il cubo di tutta la detta linea .ab. è eguale a 4. produtti, & perche (se ben ti aricordi) il primo, & ultimo di questi 4 produtti sono li cubi delle dette due parti .ac. & .cb. ... & perche il secondo produtto si forma (se ben tiari cordi) dal treppio del quadrato della .ac. sia la .cb. & perche tal treppio è satto con la multiplicatio ne satta per 3. per memoria di questa multiplicita, ouero tripplicita, notaremo questo 3 di dentro del detto secondo spacio (ma dalla banda sinistra) & perche il terzo di detti 4 produtti si forma con quel medesimo ordine, che vien formato il secondo (ma per modo contrario) cioe el si forma con il treppio del quadrato della parte .cb. sia la parte .ac. & pero per memoria di questa multiplicita notaremo vn'altro 3 da l'altra banda (cioe dalla destra) nel detto secondo spacio, come nella figura vedi. (General Trattato, Part II, Book 2, p. 69v)
that the cube of such a line ab equals four products, and because (if properly remembered), the first, and last of these four products are the cubes of the parts ac and cb ... and because the second product is formed (if properly remembered) by three times the square of ac times cb and because this product comes from multiplying by three. To remember that product we'll put this three inside the second cell from the left and because the third of the four products is formed in the same way as the second (but in the opposite order), it equals three times the square of cb times ac, so we put another three in the second cell from the right, as shown in the figure. (Translation by Stefania Sani and me.)
Next Tartaglia takes up calculations with square roots, as shown in these three examples:

piu means plus in the circled expression and the odd capital R symbol with an arrow through the leg is a square root sign — \( \sqrt{} \) as we write it. So the calculation is:
\begin{align}
(5 + \sqrt{3})^2 &= (5 + \sqrt{3}) \cdot (5 + \sqrt{3})\\
&= 5^2 + 2 \cdot 5 \cdot \sqrt{3} + \sqrt{3}^2\\
&= 25 + 10 \sqrt{3} + 3\\
&= 28 + \sqrt{300}
\end{align}
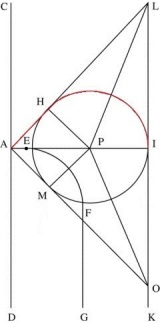
Note that immediately above the examples Tartaglia refers to Euclid II, 4 (per la detta quarta del secondo di Euclide):
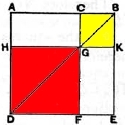
Euclid II, 4: If a straight line be cut at random, the square on the whole is equal to the squares on the segments and twice the rectangle contained by the segments.
When Euclid talks about a square here, he means the area of the square and the same for the rectangles. So this is a statement about areas, and that is how Tartaglia views the squaring of an expression like \( x + y, \) switching to modern notation. Let \( x = AC = HG\) be the side of one of the smaller squares and \( y = CB = CG\) the side of the other. Then \( (x+y)^2 = (AC+CB)^2 = AB^2 \) is "the square on the whole" and:
\begin{align}
AB^2 &= (AC+CB)^2\\
&= \color{red}{HG^2} + CB^2 + 2 \cdot AC \cdot CG\\
&= \color{red}{AC^2} + CB^2 + 2 \cdot AC \cdot CB\\
\end{align}
That is:
\[ (x+y)^2 = x^2 + y^2 + 2xy. \]
Tartaglia was immersed in Euclid whom he taught and translated into the vernacular, so this was a natural way for him to think and illustrates the emergence of the new algebra from classical geometric ideas and texts.
Part IV concerns triangles, regular polygons, the Platonic solids, and Archimedean topics like the quadrature of the circle and circumscribing a cylinder around a sphere. In Part IV, Book 1 (p. 24v), he gives Ptolemy's old figure in his table of chords in the Almagest for the side of a regular decagon inscribed in a circle of radius 60. Ptolemy's value for the side of the decagon is \( 37 : 4' : 55'' \) using the astronomers' old notation of minutes and seconds — parti \( 37 .\) m \( . 4 . \) \( \frac{1}{2} . 55 \) as Tartaglia writes it in the circled extract. This is the sexagesimal or base sixty notation we still use in measuring time and angles: \( 37 : 4' : 55'' = 37 + \frac{4}{60} + \frac{55}{60^2} = 37 + \frac{4}{60} + \frac{55}{3600} = 37.0819 \; 4444 ,\) the last being its equivalent in decimal notation. The correct ratio of side to radius for the regular pentagon is \( 1 / \varphi = 0.6180 \; 33988, \) where \( \varphi = \frac{\sqrt{5}+1}{2} \) is the golden ratio, so if \( d \) is the side of the regular decagon inscribed in a circle of radius \( 60, \) then:
\begin{align}
d &= \frac{1}{\varphi} \cdot 60\\
&= 0.6180 \; 33988 \cdot 60\\
&= 37.0820 \; 3933\\
&= 37 : 4' : 55'' : 20'''\\
\end{align}
This shows that Ptolemy's value is correct to the nearest second, that final \( 20 \) on the last line indicating \( \frac{20}{60}'' = \frac{1}{3}''; \) that is, one third of a second. Ptolemy's value to three sexagesimal places errs from the actual value by \( 10^{-4}; \) in other words, it is correct to one part in ten thousand, not bad for ~150 AD, when Ptolemy flourished.
To calculate the side of the regular pentagon from that of the decagon, Tartaglia proceeds to cite Euclid XIII, 10:
Euclid XIII, 10: If an equilateral pentagon be inscribed in a circle, the square on the side of the pentagon is equal to the squares on the side of the hexagon and that of the decagon inscribed in the same circle.
That is to say:
\begin{align}
p^2 = r^2 + d^2,
\end{align}
where p is the side of the decagon, r is the radius of the circle (which is the same as the side of the hexagon), and d is the side of the decagon. He first performs the calculation on the right:
\begin{align}
p^2 &= r^2 + d^2\\
&= 60^2 + (37 : 4' : 55'')^2\\
&= 3600 + 1375 : 4' : 14''\\
&= 4975 : 4' : 14''.
\end{align}
The notation in this calculation is mine, but the values are Tartaglia's, and they are correct to the nearest second. He then says that \( p = \sqrt{4975 : 4' : 14''} = 70 : 32' : 3'', \) this too being correct to the nearest second. It would be good to know how Tartaglia calculated square roots of sexagesimal values, maybe it's buried somewhere in the Trattato. It might have been trial-and-error — in this case, it's easy to see that \( 4975 \) is about midway between \( 70^2 = 4900 \) and \( 71^2 = 5041, \) so \( \sqrt{4975} \sim 70 : 30'. \) The actual value is calculated like this:
\begin{align}
p &= {\sqrt{{5 - \sqrt{5}} \over {2}}} \cdot r\\
&= 1.1755 \; 70505 \cdot 60\\
&= 70.5342 \; 3028\\
&= 70 : 32' : 3'' : 13''',
\end{align}
so Tartaglia's final result also is correct to the nearest second. Sixteenth century mathematicians were at the mercy of sexagesimal notation and calculations when fractions wouldn't do. Tartaglia just missed Simon Stevin's epochal invention of decimal fraction notation in 1585 and surely would have appreciated it.
Tartaglia was capable of exact calculations in this vein, as shown by his figures for the Platonic solids later in Part IV, where he gives the side length of each solid when inscribed in a sphere. He assumes a sphere of radius \( 6 \) (Sel diametro della sphera sara \( 12 \) / If the diameter of the sphere is \( 12 \)) and gives the side length for the regular tetrahedron as \( \sqrt{96} \) (Il lato del quattro base sara \( \sqrt{96} \) / The side of the solid with four bases is \( \sqrt{96} \)).
| Figure | side / radius | As decimal |
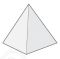
Tetrahedron
|
\( \sqrt{96} / 6 \) | \( 1.6329 \; 93162 \) |
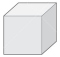
Cube
|
\( \sqrt{48} / 6 \) | \( 1.1547 \; 00538 \) |
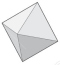
Octahedron
|
\( \sqrt{72} / 6 \) | \( 1.4142 \; 13562 \) |
All of Tartaglia's values are correct; here are the first three. In discussing these results, he cites Book XIII of Euclid, where the Platonic solids are all constructed and many relationships among them derived — that the inscribed cube actually sits inside the inscribed dodecahedron, for example, some of the dodecahedron's vertices being connected to describe the cube (in Book XIII, 17, Euclid inverts this point of view, constructing the dodecahedron by building little pup tents on the faces of the cube). In Book XIII, 18, Euclid sets out the sides of all five figures inscribed in a single sphere, comparing them to each other in one diagram in the plane. In his commentary on this proposition, Heath gives the figures' sides as a function of the radius (for the tetrahedron, he has that the side = \( \frac{2}{3} \sqrt{6} \cdot \text { radius}, \) for example, this expression being equivalent to \( \sqrt{96} / 6, \) as appears in the chart here).
The tetrahedron and cube calculations are straightforward, but perhaps the octahedron is simplest. Cut the octahedron in half by a plane making two mirrored pyramids and two equal hemispheres. The cross-section contains a square in a circle: the vertices of the square are vertices of the octahedron and the circle is a great circle of the sphere. The diameter of the circle is the diameter of the sphere and the side of the square is the side of the octahedron. For a square, the ratio of a side to a diagonal (which is the same as the diameter of the circumscribing circle) is \( \sqrt{2} / 2, \) so the ratio of a side to the radius of the circle is \( \sqrt{2}. \) It follows that \( \sqrt{2} \) is also the ratio of a side of the octahedron to the radius of its circumscribing sphere. If the diameter is \( 12, \) as Tartaglia assumes, then the side is \( 6 \sqrt{2} = \sqrt{72} \) as he says.
What a travesty that Tartaglia is mainly known today for finding the roots of cubic polynomials, at least in the English-speaking world. Even this accomplishment is used against him, latter-day partisans taking Cardano's side in their dispute. Only the most tortuous backtracking assigns such central importance to solving the cubic. This line of research stalled in the sixteenth century, quartic or fourth degree polynomials being the last to be solved. The problem languished, to be taken up over two hundred years later by Lagrange and others in the late eighteenth century, culminating in the work of Abel and Galois proving the impossibility of a general solution to the quintic. But to think the question drove the development of mathematics in the interim is wildly anachronistic, testament to an cramped, internalist notion of the history of mathematics.
A modern approach looks for values of \( x \) satisfying:
\begin{equation}{
x^3 + ax^2 + bx + c = 0, \hskip{40px} a, b, c \in \mathbb{R}.
}\tag{0} \end{equation}
Such values of \( x \) are called roots of the equation. The Fundamental Theorem of Algebra says there are three roots in the complex plane for any \( a, b, c \in \mathbb{R}, \) and the task is to express them in terms of \( a, b, \) and \(c \) (two of the roots may be complex numbers, but at least one of them is real). Such an approach was completely foreign to Tartaglia, working before modern algebraic notation or even wide acceptance of negative numbers. He addressed the problem in 1546 in Book IX of Quesiti et inventioni diverse (Questions and Assorted Discoveries), where he collected a series of letters written to him with questions, together with his answers. He regarded these three equations as different, for example:
\begin{equation}{x^3 + 3x = 10 \hskip{15px} \text{Type I,}}\tag{1} \end{equation}\begin{equation}{x^3 = 3x + 10 \hskip{15px} \text{Type II,}}\tag{2} \end{equation}\begin{equation}{x^3 + 10 = 3x \hskip{15px} \text{Type III.}}\tag{3} \end{equation}
He always worked in examples and expressed algorithms verbally. He sent a poem to Cardano on March 25, 1539 as part of Quesito XXXIIII explaining his solution to these three equations:[22]
The translation of this poem is mine, based on that of Friedrich Katscher. cose or cosa is "the thing", namely, the sought for number, what we denote by \( x. \) Let's go through the poem to explain the solution:
1) Quando chel cubo con le cose apressò (When the cube with the cosa beside it). This looks like \( x^3 + x, \) but it's going to be \( x^3 + 3x. \)
2) Se agualia à qualche numero difereto (Equals some other whole number). This sets the equation. Suppose the "other whole number" is \( 10, \) making the equation \( x^3 + 3x = 10. \)
3) Trouan dui altri differenti in esso (Find two other, of which it is the difference). Find two values \( u \) and \( v \) such that \( u - v = 10. \)
4) Cb'el lor produtto sempre sia eguale / Al terzo cubo delle cose neto (To put their product equal / To a third of the cosa, all cubed). The other condition on \( u \) and \( v \) is that \( u \cdot v = (3/3)^3 = 1^3 = 1. \)
5) El residuo poi suo generale / Delli lor lati cubi ben sottratti / varra la tua cosa principale (Then the difference / Of their cube roots, properly subtracted / Will be the value of your first unknown). The root is \( x = \sqrt[3]{u} - \sqrt[3]{v}. \)
Let's stop there, after the first three stanzas. Tartaglia is showing how to solve a Type I equation:
\begin{equation}{x^3 + 3x = 10.}\tag{1} \end{equation}
He says to find values \( u \) and \( v \) such that:
\begin{align}
&u - v = \color{red}{10}, \hskip{15px} \text{and}\\
&u \cdot v = \color{red}{3}/3 = 1,
\end{align}
where the \( \color{red}{10} \) and \( \color{red}{3} \) are the constant on the right side and the coefficient of \( x \) in equation (1) respectively. Eliminating \( v \) from this little system produces a quadratic equation in \( u, \) which Tartaglia solves operando per Algebra (using Algebra) to find:
Quesiti, Book 9, p. 124r.
\begin{align}
u &= \sqrt{26} + 5,\\
v &= \sqrt{26} - 5.\\
\end{align}
Note that all the numbers are positive. Subtraction is allowed, like with \( v = \sqrt{26} - 5, \) but the result must be positive. The root of equation (1) is then:
\begin{align}
x &= \sqrt[3]{u} - \sqrt[3]{v}\\
&= \sqrt[3]{\sqrt{26} + 5} - \sqrt[3]{\sqrt{26} - 5}.
\end{align}
To see that this value of \( x \) satisfies the equation, plug it in:
\begin{align}
x^3 + 3x &= (\sqrt[3]{u} - \sqrt[3]{v})^3 + 3 (\sqrt[3]{u} - \sqrt[3]{v})\\
&= \left[u -3(\sqrt[3]{u})^2 \sqrt[3]{v} + 3\sqrt[3]{u} (\sqrt[3]{v})^2 - v\right] + 3 (\sqrt[3]{u} - \sqrt[3]{v})\\
&= \left[u -3\sqrt[3]{u} \sqrt[3]{v} \left(\sqrt[3]{u} - \sqrt[3]{v}\right) - v\right] + 3 (\sqrt[3]{u} - \sqrt[3]{v})\\
&= \left[u -3\sqrt[3]{uv} \left(\sqrt[3]{u} - \sqrt[3]{v}\right) - v\right] + 3 (\sqrt[3]{u} - \sqrt[3]{v})\\
&= \left[u -3 \cdot 1 \left(\sqrt[3]{u} - \sqrt[3]{v}\right) - v\right] + 3 (\sqrt[3]{u} - \sqrt[3]{v})\\
&= u - v\\
&= 10.
\end{align}
The conditions on \( u \) and \( v \) now makes sense: they were chosen precisely to get all the cancellation in the final steps. The second line expands the binomial to the third power. After regrouping, we notice the appearance of \( \sqrt[3]{uv}, \) which is just \( 1 \) by the condition on \( u \) and \( v. \) Additive cancellation gets us to the next to the last line, \( u - v, \) which is just \( 10 \) by the other condition on \( u \) and \( v. \) What's nice about this is that you get an idea of how Tartaglia came up with it, having been playing around with binomial expansions for years.
The middle stanzas of the poem, starting with In el secondo de cotesti atti / In the second kind of equation, show how to solve an equation of Type II:
\begin{equation}{x^3 = 3x + 10.}\tag{2} \end{equation}
The only difference compared to the first kind of equation is that you set the sum of \( u \) and \(v \) equal to \( 10. \) The final stanzas, starting with El terzo poi de questi nostri conti / The third type of equation say that solving Type III equations is the same as for Type II.
| Type I: | \( b \) positive | \( c \) negative |
| Type II: | \( b \) negative | \( c \) negative |
| Type III: | \( b \) negative | \( c \) positive |
The three types of equations amount to finding a positive root of:
\begin{align}f(x) = x^3 + bx + c\end{align}
when \( b \) and \( c \) are positive and negative in different combinations. Note this is the general equation (0) above with no quadratic term (that is, \( a = 0 \)). \( c \) is negative for Type I and II equations, so \( f(0) = c < 0. \) But \( f(x) \rightarrow \infty \text{ as } x \rightarrow \infty, \) showing that \( f(x) \) always has a positive root for Type I and II equations. This is not always the case for Type III equations though. For example, consider:
\begin{equation}{x^3 + 10 = 3x,}\tag{3} \end{equation}
which has one negative real root and two complex roots. Like Tartaglia says, the solution for Type II equations works equally well for Type III, you just have to accept negative roots in some cases (which he doesn't). A simple transformation unknown to Tartaglia removes the quadratic term in equation (0), so his solutions are very close to the general solution. Compare with Euler's treatment two hundred years later in his Elements of Algebra, now fortified with a full algebraic apparatus but containing many examples and special cases just as the old maestro had done so many years earlier.
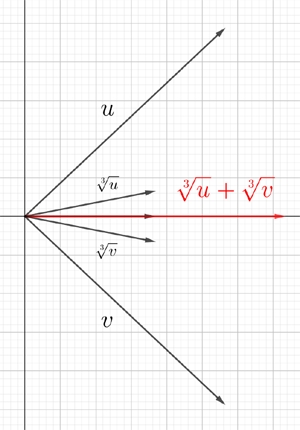
In a letter of August 7, 1539, Cardano asks Tartaglia about solving the type II equation \( x^3 = 9x + 10 \) (.1. cubo, equale à .9. cose ріu .10.). Tartaglia's method leads to:
\begin{align}
&u + v = 10,\\
&u \cdot v = (9/3)^3 = 3^3 = 27,
\end{align}
solving which leads to \( u = 5 + 2i, v = 5 - 2i, \) complex numbers with imaginary components as pictured here. The marvel is that Tartaglia's solution still works because \( \sqrt[3]{u} \) and \( \sqrt[3]{v} \) are complex conjugates (as \( u \) and \( v \) are), so the imaginary components cancel. It turns out that this equation has one positive root at \( x = \sqrt{6} + 1 \) and Tartaglia was well capable of verifying it were the root given. Of course complex numbers and calculations involving them were foreign to him and it took hundreds of years for mathematicians to become comfortable with them, a firm foundation not being set down until Wessel's work, first published in 1799, 250 years after Tartaglia. Targaglia's bête noire Cardano did write presciently about complex numbers in 1545 in Artis magnae when trying to solve:
\begin{align}
&u + v = 10,\\
&u \cdot v = 40,
\end{align}
a system plainly motivated by this work with cubic equations. Cardano correctly identified the solutions as \( 5 \pm \sqrt{-15}, \) noting that such values are as accurate as they are useless (adeo est subtile, ut sit inutile).
All the same, Tartaglia's priority claims regarding the cubic equation are sustained by Satyanad Kichenassamy in a recent article, where he argues that Tartaglia knew how to solve equations like \( x^3 + 6x^2 = 100 \) as early as 1530, a different class from those above where now there is a quadratic term but no linear term.[23] Kichenassamy's exemplary textual and contextual analysis emphasizes Tartaglia's reliance on the continued proportions approach of Luca Pacioli, a predecessor well known to Tartaglia and much cited in the General Trattato.
Tartaglia's poem illustrates another aspect of his writing, namely, how good it is, including his Dantean hendecasyllable, terza rima (eleven syllable, interlocking three-line rhyming) verses[24] which cogently express a three-pronged algorithm decipherable all these years later across a language barrier. Tartaglia has been pilloried for his language, starting in his own lifetime — Arielle Saiber has a catalog of slanders (disadorna [unadorned], rozza e dialettale [coarse and full of dialect], ributtante [disgusting], barbaro [barbarian], and so on).[25] A strong element of snobbery is detectable, often from well-trained and well-paid humanists who emancipated themselves from the university monopoly but not from class prejudice. Tartaglia's use of colloquial and clear language, addressed to a broad public, was itself a transgression to these purveyors of eloquence, it seems, as if meaning is subsidiary, and greatly so, to mode of expression. It is Tartaglia's echo that is recognizable to the modern ear though, not theirs (see Zilsel's remarks about Tartaglia's modernity in footnote 2 below).
The term "renaissance" was coined much later, but Tartaglia might have appreciated the tribute, immersed in classical mathematics as he was. Cradled in "the city circled by the sea", he strove to reorganize the ancient ways of thinking and present the new science and mathematics to an increasingly literate and numerate public. Venice produced him, but his influence extended far beyond his time and place as printing drove a confident Europe-wide scientific culture.
Several aspects of Tartaglia's work are foreign to modern mathematical sensibilities: the unabashed and extensive work on business mathematics, the lack of modern algebraic and decimal notation, the unwillingness to accept complex or even negative numbers, the constant appeal to Euclid in numerical work, the narrative style and lack of proofs, the use of examples to carry a point. Imagination is necessary to put him in context, to appreciate how he forwarded so many areas of mathematics in spite of the weakness of the tools at his disposal. Forwarded the subject, connected it to areas of practical interest, and disseminated it to a broad public active outside the universities. Tartaglia is different from us, but the wonder is how recognizable he is, properly understood, and how much he helped shape our world.
Mike Bertrand
July 20, 2019
In memory of Alvin Cline Bertrand (July 20, 1914 — January 6, 1995), another son of the working-class who appreciated mathematics.
^ 1. "Cardano v. Tartaglia: The Great Feud Goes Supernatural", by Tony Rothman, Mathematical Intelligencer, 36 4 (Winter 2014), pp. 59-66. This invaluable essay restores a much-needed balance, elevating Tartaglia to the first rank and conscientiously redressing a long history of malice and outright fabrication at Tartaglia's expense.
^ 2. The Social Origins of Modern Science, by Edgar Zilsel (edited by Diederick Raven, Wolfgang Krohn, and Robert S. Cohen), Kluwer Academic Publishers (2000), ISBN 0-7923-6457-0. Zilsel regarded Tartaglia and Simon Stevin (1548-1620) as "the two most important pioneers of scientific mechanics before Galileo" (p. 154) and wrote that Tartaglia spoke in "the voice of a representative of the true modern era" (p. 35). Zilsel's dates are 1891-1944. Most of these essays were first published in the 1940s.
^ 3. Life in Renaissance France, by Lucien Febvre (edited and translated by Marian Rothstein), Harvard University Press (1977), ISBN 0-674-53180-9. Quotes on p. 34. These essays were originally published in French in the 1920s.
^ 4. Niccolò Tartaglia, article by Arnoldo Masotti in the Dictionary of Scientific Biography.
^ 5. "The Social Status of Italian Mathematicians, 1450-1600", by Mario Biagioli, History of Science, 27 1 (March 1989), pp. 41-95. See his penetrating observation on p. 50: "It would be interesting to ask whether a 'working class' mathematician such as Tartaglia could have ever become the Philosopher and Mathematician of the Grand Duke, had he discovered the satellites of Jupiter [as Galileo had]."
^ 6. Edgar Zilsel, Social Origins of Modern Science, p. 35.
^ 7. "Science and Patronage: Galileo and the Telescope", by Richard S. Westfall, Isis, 76 1 (March 1985) pp. 11-30.
^ 8. Metallurgy, Ballistics and Epistemic Instruments: The Nova scientia of Nicolò Tartaglia, by Matteo Valleriani, Edition Open Access / Max Planck Research Library (2013), ISBN 978-3-8442-5258-3. The quote is on p. 1. This book contains a facsimile copy of Nova scientia, the Italian and English text on facing pages, and fifty pages of helpful commentary. It is online in its entirety at the link and is also available as an inexpensive paperback.
^ 9. "How the 'New Science' of Cannons Shook up the Aristotelian Cosmos", by Mary J. Henninger-Voss, Journal of the History of Ideas 63, 3 (July 2002) pp. 371-397. "eviscerated": p. 376.
^ 10. See Nova scientia in Valleriani in (8) above, pp. 169-181. I'm closely following "Tartaglia's Ragioni: A Maestro d'Abaco's Mixed Approach to the Bombardier's Problem", by Karen J. Ekholm, British Journal for the History of Science 43 2 (2010) pp. 181-207, especially pp. 197-200.
^ 11. Tartaglia's Nova scientia in Matteo Valleriani, Metallurgy, Ballistics and Epistemic Instruments, p. 176-177.
^ 12. Mary J. Henninger-Voss, "'New Science' of Cannons", pp. 391-393.
^ 13. Paul Lawrence Rose, The Italian Renaissance of Mathematics, Librairie Droz, 1975. Rose writes that "[Moerbeke's] translation [of Archimedes] remained almost unknown for two centuries, making scarcely any impression in scholastic geometry and exercising no influence at all on scholastic mechanics or physics. In fact, a strange reversal of influence took place. Such of Archimedes' works as were known in the Arabo-Latin tradition were 'scholasticized'. Scholastics like Bradwardine and Albert of Saxony elaborated Archimedes' original geometric proofs into new logical forms, introducing quite alien philosophical and physical arguments." p. 80.
^ 14. "William of Moerbeke: Translator of Archimedes", by Marshall Clagett, Proceedings of the American Philosophical Society, Vol 126, No. 5, 1982, pp. 356-366. "It has always been my opinion": p. 356.
^ 15. Marshall Clagett, "William of Moerbeke". See pp. 362-3 for the authorship of Moerbeke.
^ 16. The development of Euclidean axiomatics: The systems of principles and the foundations of mathematics in editions of the Elements in the Early Modern Age, by Vincenzo De Risi, Arch Hist Exact Sci. 2016, 70(6), pp. 591–676. "following some twenty years later": p. 597.
^ 17. "Euclid’s Swan Song: Euclid’s Elements in Early Modern Europe", by Antoni Malet, pp. 205-234 in Greek Science in the Long Run: Essays on the Greek Scientific Tradition (4th c. BCE-17th c. CE), edited by Paula Olmos, Cambridge Scholars Publishing (2012), ISBN (10) 1-4438-3775-X, ISBN (13) 978-1-4438-3775-0. "mathematically cogent": p. 207.
^ 18. Mary J. Henninger-Voss, "'New Science' of Cannons", p. 392.
^ 19. Capitalism and Arithmetic: The New Math in the 15th Century, by Frank J. Swetz, Open Court Publishing Company (1987), ISBN 0-8126-9014-1. Includes the full text of the Treviso Arithmetic of 1478, translated into English by David Eugene Smith. The Treviso Arithmetic was the first printed arithmetic, published some eighty years before the General Trattato in the Venetian municipality of Treviso and takes up 139 pages in Swetz's book, his helpful commentary comprising the remaining 200 pages. The Treviso Arithmetic exemplifies the commercial tradition, already mature in 1478, that spawned Targaglia and the problems are similar to those in Part I of the General Trattato.
^ 20. The parts of the General Trattato are all available at Google Books: Part I, Part II, Part III, Part IV, Part V, Part VI. The entire General Trattato can be downloaded as a pdf at ETH-Bibliothek.
^ 21. History of Mathematics, Volume 1, by David Eugene Smith, Dover Publications, Inc. (1923). See p. 298 for quote on Tartaglia.
^ 22. See Friedrich Katscher's highly informative series in MAA Convergence for August, 2011, "How Tartaglia Solved the Cubic Equation". Katscher translates the poem into English and provides a mathematical analysis of the poem and Tartaglia's solution generally.
^ 23. "Continued proportions and Tartaglia’s solution of cubic equations", by Satyanad Kichenassamy, Historia Mathematica 42, (2015) pp. 407–435.
^ 24. Measured Words: Computation and Writing in Renaissance Italy, by Arielle Saiber, University of Toronto Press (2017), ISBN 978-0-8020-3950-7. Saiber's literary analysis of Tartaglia's poem singles it out for special consideration in a context where such productions were not unheard of. She takes up four ""beautiful minds" at the intersection of mathematics and literature: Leon Battists Alberti, Luca Pacioli, Tartaglia, and Giambattista Della Porta. The bibliography is first rate. hendecasyllable, terza rima verses: p. 109.
^ 25. Ibid., p. 125.