Cauchy on Permutations and the Origin of Group Theory

The history of any subject is like a great river, the central channel meandering but ultimately driving down to the sea, with side branches veering off here and there along the shore to make their own way. Some of those rivulets find their way back to the main course, others peter out in a swamp, the two exchanging places as blockages and torrential rains come into play. Powerful underground springs interact with topography and gravity to govern the web of flowing water in mysterious ways. And all changing year by year as Mark Twain said of the old Mississippi.
Cauchy's early work on permutations was pivotal in the literal sense of that word. He harkened back to the preoccupations and problems of predecessors immediate and remote, recasting them into a new framework whose foundations last to this day and constitute the essential basis of group theory. Granted, everything in sight is a permutation group and it took some time for an abstract group theory to form and emancipate itself from early origins, even to outgrow the connection with algebraic functions and the term substitution (Cauchy's term for permutation). Camille Jordan's path-breaking book in 1870, for example, was titled Traité des substitutions et des équations algébriques, Eugen Netto's in 1882 Substitutionentheorie und ihre Anwendung auf die Algebra.
The task is to unwind the story as it actually unfolded, to expose the driving dynamics of the time and try to see things as the old ones did themselves. All the same, some old channels run so directly down to the present day that it is pointless to overlook their anticipatory value from early on; even the most inveterate antiquarian must acknowledge the genesis of a modern approach.
Cauchy published two early memoirs on permutations in January 1815, exactly two hundred years ago. He acknowledged Lagrange and other predecessors in this work, reframing their findings and building on them. This article concerns Cauchy's first memoir published in the Journal de l'École polytechnique (founded in Germinal, Year 3!). It is titled Memoire Sur le Nombre des Valeurs qu'une Fonction peut acquerir, lorsqu'on y permute de toutes les manieres possibles les quantites qu'elle renferme (Memoir on the number of values that a function can acquire when the variables it contains are permuted in all possible ways). The first link is to the original article from 1815, the second to my English translation.[1]

Cauchy's starting point, like that of earlier workers, was permuting the roots of polynomial equations with integer coefficients in hope of finding algebraic formulas giving the roots in terms of the coefficients. "Algebraic" here means addition, subtraction, multiplication, division, and taking roots. Think of the quadratic formula, known in essence to the Babylonians, but also the formulas for third and fourth degree polynomials discovered in the 16th century. But there progress stopped for 250 years, the quintic stymieing all efforts at solution. Those efforts were considerable and the failure a source of growing frustration as the power and depth of mathematical methods increased to unheard-of heights, calculus and all the rest, but still no solution to the quintic in 1815.
Vandermonde and especially Lagrange made a valiant start in two separate papers in 1771, as Cauchy says in the first sentence, and Ruffini almost pushed home a proof of the insolvability of the quintic based on their work. Ruffini polished his proof over the period 1799-1804 and expert consensus is that he never got all the way there, but it's hard to tell because very few people have been willing to wade through the mountains of paper he produced; the stream got diverted and poor Ruffini was left stranded — see Hans Wussing's appreciation of Ruffini in his highly regarded book on the history of group theory.[2] Abel published a six page paper on the insolvability of the quintic in 1824 generally acknowledged as a solid proof, schematic though it was.
Cauchy is very much in the main channel, here as elsewhere. Consider a function of several variables (quantités), he says, and consider how many values (valeurs) the function can take by rearranging the variables in all possible ways. He means by the value of a function an inherently different function, so these two functions, for example, have the same value:
\[ K' = {a_1 + a_2}, \hskip{20px} K'' = {a_2 + a_1}, \]
where \( K' \) and \( K'' \) are derived from each other by swapping \( a_1 \) and \( a_2 \) in \( {K(x_1, x_2)} = {x_1 + x_2} \). But the following two functions do not have the same value when \( a_1 \) and \( a_2 \) are swapped in their template function \( {L(x_1, x_2)} = {x_1 + \cos{x_2}} \):
\[ L' = {a_1 + \cos{a_2}}, \hskip{20px} L'' = {a_2 + \cos{a_1}}. \]
So function \( K \), thought of as a function of \( 2 \) variables, has one possible value, while function \( L \) has two possible values. Cauchy's purpose is to examine this problem for any number of variables \( n \) — to find the range of possible values functions can have and, in particular, to see if that range is restricted. As just shown, for \( n = 2 \), there are functions with one value and functions with two values.
Cauchy uses the term permutation for a rearrangement of symbols and thinks of permutations as acting on a template function like just explained. His notation for a permutation is:
\[ 1 \ . 2 \ . 4 \ . 3, \]
and then a substitution is one permutation on top of the other, like this:
\[ \begin{pmatrix}
1 \ . 2 \ . 4 \ . 3 \\
2 \ . 4 \ . 3 \ . 1 \\
\end{pmatrix} , \]
where \( 1 \to 2, 2 \to 4 \), and so on. The two row configuration is identical to modern notation for a permutation except for the periods, and Cauchy originated it in this paper. Later in the memoir he drops the periods when indices are represented by variables \( \alpha, \beta, \gamma \) and so on.
How about for \( n = 3 \) — are there functions with one, two, three, four, five, and six values? Note that's the extent of what's possible, because there are only \( {1 \cdot 2 \cdot 3} = 3! = 6 \) possible ways of arranging three letters \( (a_1, a_2, a_3) \). Consider \( {K(x_1, x_2, x_3)} = {x_1 + x_2 + \cos{x_3}} \) in order to follow Cauchy's findings. The six functions arising from replacing the variables with all permutations of \( (a_1, a_2, a_3) \) are:
\[ \Biggl\{
\begin{array}{lr}
K_1 &= a_1 + a_2 + \cos{a_3} \\
K_2 &= a_2 + a_1 + \cos{a_3} \\
\end{array} \Biggr.
\]
\[ \Biggl\{
\begin{array}{lr}
K_3 &= a_1 + a_3 + \cos{a_2} \\
K_4 &= a_3 + a_1 + \cos{a_2} \\
\end{array} \Biggr.
\]
\[ \Biggl\{
\begin{array}{lr}
K_5 &= a_2 + a_3 + \cos{a_1} \\
K_6 &= a_3 + a_2 + \cos{a_1} \\
\end{array} \Biggr.
\]
Each \( K_{\alpha} \) arises from a corresponding permutation; \( K_4 \) arises from permutation \( A_4 = 3 \ . 1 \ . 2 \), for example. The six functions can be broken into three blocks.
Each of the three blocks determines a different value of \( K \), there are only three total, and \( K \) has the same value within a block. Take a function from one of the blocks — say \( K_1 \) from the first block. Some substitution takes you from \( K_1 \) to \( K_2 \) in its block — namely, the transposition \( (1 \ 2) \) (the very term and notation employed by Cauchy incidentally, except he put a comma between the two indices). The same substitution acting on the indices takes you from \( K_3 \) to \( K_4 \) and from \( K_5 \) to \( K_6 \), because if permuting those variables in the first block didn't change the value, then the same is the case within the second or third block. The value for each block is different, but the same sequence of substitutions running through each block leaves that value unchanged.
In this case there are only two functions in each block, but in general, the same sequence of substitutions taking you through the first block, however large, takes you through each of the others. This shows that the blocks are all the same size and since they partition the set of all functions, the number of values it is possible for a function on \( 3 \) variables to take is a factor of \( 3! = 6 \); and by the same logic, the number of values it is possible for a function on \( n \) variables to take is a factor of \( n! \). For \( n = 3 \), there are functions taking three values and two values (eg, \( K = a_1 - a_2 \)), but not four or five values. Lagrange proved this for polynomials in his Réflexions sur la résolution algébrique des équations in 1771, and Cauchy credits Ruffini as well. In fact, this is the germ of Lagrange's Theorem, that in a finite group, the order of a subgroup divides the order of the group. In this example, \( \{A_1, A_2\} \) is a subgroup of \( S_3 \), the group of all substitutions on three letters, and the other two blocks are its cosets.
Next Cauchy takes a departure to state and prove his main result, which was new:
Theorem: The number of different values of a non-symmetric function of n variables cannot be less than the largest prime number p contained in n without becoming equal to 2.
He employs the notation:
\[ \begin{align*}
N &= {1 . 2 . 3 ... n} , \\
R &= \mathrm{number\ of\ different\ values\ the\ function\ can\ take,} \\
M &= \mathrm{size\ of\ each\ block;}
\end{align*} \]
so in the foregoing example, \( n = 3,\: N = 3! = 6,\: R = 3,\: M = 2 \). Note that \( {R \cdot M} = N \), as developed above. Let's walk through another example to exemplify the theorem, with \( {K(x_1, x_2, x_3, x_4, x_5)} = { x_1 x_2 + x_3 x_4 + x_5} \). We have \( n = 5,\: N = 5! = 120 \) for this function. Since the largest prime less than or equal to \( n \) is now \( p = 5 \), the theorem asserts that this or any other function cannot take a total of three or four values; ie, \( R \neq 3 \) and \( R \neq 4 \) for this function. Here are a few \( Ks \) with different values:
\[ K_1 = {a_1 a_2 + a_3 a_4 + a_5} \\ K_2 ={a_1 a_4 + a_2 a_3 + a_5} \\ K_3 = {a_1 a_3 + a_2 a_4 + a_5}. \]
Each one is associated with a block of functions, or substitutions if you will, giving the same value. \( K_1 \), for example is associated with
\[ K_1' = {a_4 a_3 + a_1 a_2 + a_5}, \]
where \( K_1 \) and \( K_1' \) are identified respectively with the substitutions:
\[ \begin{pmatrix}
1 \ 2 \ 3 \ 4 \\
1 \ 2 \ 3 \ 4
\end{pmatrix} ,
\begin{pmatrix}
1 \ 2 \ 3 \ 4 \\
4 \ 3 \ 1 \ 2
\end{pmatrix} .\]
I'm leaving out the \( 5 \) even though they are substitutions on \( 5 \) letters, because the \( 5 \) is always unchanged for the first block (and the other two shown for that matter). It looks like there will be another four blocks like this, where each of \( a_4, a_3, a_2, a_1 \) plays the role of that last summand sitting at the end of \( K \); that is, it looks like \( R = 15 \) and therefore \( M = {120 / R} = {120 / 15} = 8 \). If so, \( K \) certainly satisfies the theorem.
Let's examine the substitutions in the same block as \( A_1 \), that is, the substitutions on the indices leaving \( K_1 \) unchanged. It's clear that \( a_5 \) has to be retained as a summand at the end; also that the product \( x_1 x_2 \) or \( x_2 x_1 \) must be a summand and since the pair can be the first product or the second one, that's four possibilities, four different substitutions. The other product can be either \( x_3 x_4 \) or \( x_4 x_3 \), so there are eight substitutions all told leaving \( K_1 \) unchanged and \( M = 8 \). This squares with there being fifteen different values: \( {R \cdot M} = {15 \cdot 8} = 120 = N \). Here are the eight substitutions just described, the ones leaving the value of \( K_1 \) unchanged:
\[ \begin{pmatrix}
1 \ 2 \ 3 \ 4 \\
1 \ 2 \ 3 \ 4
\end{pmatrix} ,
\begin{pmatrix}
1 \ 2 \ 3 \ 4 \\
2 \ 1 \ 3 \ 4
\end{pmatrix} ,
\color{red}{
\begin{pmatrix}
1 \ 2 \ 3 \ 4 \\
1 \ 2 \ 4 \ 3
\end{pmatrix}} ,
\begin{pmatrix}
1 \ 2 \ 3 \ 4 \\
2 \ 1 \ 4 \ 3
\end{pmatrix} , \\
\begin{pmatrix}
1 \ 2 \ 3 \ 4 \\
3 \ 4 \ 1 \ 2
\end{pmatrix} ,
\begin{pmatrix}
1 \ 2 \ 3 \ 4 \\
3 \ 4 \ 2 \ 1
\end{pmatrix} ,
\begin{pmatrix}
1 \ 2 \ 3 \ 4 \\
4 \ 3 \ 1 \ 2
\end{pmatrix} ,
\begin{pmatrix}
1 \ 2 \ 3 \ 4 \\
4 \ 3 \ 2 \ 1
\end{pmatrix} . \]
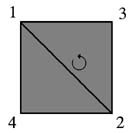
This block is a group, namely \( D_4 \), the dihedral group of order four, or the rigid motions of a square. To see this, number the corners of a square as shown and identify a rigid motion with its effect on the indices, thought of as a substitution. The motion suggested in the diagram rotates the square around the diagonal in the third dimension, the final figure being identical to the original one, but with the front going to the back and vice versa. Corners \( 1 \) and \( 2 \) are unchanged, but \( 3 \) and \( 4 \) are swapped (transposed). That's the red substitution above, and there is a similar interpretation for each of the eight substitutions.
Here is the genesis of group theory, because it is evident that if two different substitutions leave \( K \) unchanged when applied separately, then they will also leave \( K \) unchanged when applied one after the other. In other words, the block of substitutions leaving \( K \) unchanged is closed under the operation of substitution multiplication. It's an innocent start, the group showing up incidentally as a aid to studying the functions and how many different values they can take. Cauchy here and his predecessors had proved, at least for symmetric groups, that the order of a subgroup divides the order of the group, as does its index. That is exactly the word Cauchy uses for the value motivating his memoir: J'appellerai désormais indice de la fonction \( K \), le nombre \( R \) qui indique combien cette fonction peut obtenir de valeurs essentiellement différentes (I now call the index of the function \( K \) the number \( R \) which indicates how many essentially different values this function can take).
Returning to the original five indices in this example, note that there is at least one substitution of order \( p = 5 \), namely:
\[ P = \begin{pmatrix}
1 \ 2 \ 3 \ 4 \ 5 \\
2 \ 3 \ 4 \ 5 \ 1
\end{pmatrix} . \]
Like Cauchy, we apply substitutions left to right (apply the one on the left first, then the one on the right). Multiply the substitutions in the block by \( P \) on the right to obtain another block, and these are all the substitutions for another value of \( K \), an instance of which is \( K_2 = a_2 a_3 + a_4 a_5 + a_1 \), which is the first substitution in the original block (the identity substitution) multiplied by \( P \). Then multiply all the substitutions in the original block by \( P^2 \) to obtain still a third block, and so on. The five blocks obtained are all disjoint. We happen to know in this example that \( M = 8 \), but if we didn't, the foregoing analysis implies that \( M \) can't be too large and therefore that \( R \) can't be to small, since \( {R \cdot M} = 120 \). In particular:
\[ \begin{align*}
5M &\leq 120 = {M \cdot R} \\
\therefore R &\geq 5
\end{align*} \]
To prove the blocks are disjoint, suppose that for some \( d_1, d_2 \in D_4 \) and \( 0 \leq r, s < 5 \),
\[ {d_1 P^r} = {d_2 P^s}. \]
Exchanging indices if necessary:
\[ d_1 = {d_2 P^t}, \]
where \( 0 \leq t < 5 \).
\[ \therefore P^t = {d_2^{-1} \cdot d_1} = d_3 \in D_4. \]
The left side has order 5, the right side order \( 2 \) or \( 4 \), unless both are the identity, which must be the case, because an element can't have two different orders. It follows that \( t = 0 \) and \( d_1 = d_2 \), proving disjointness. I'm cheating in a couple ways here, using modern machinery and facts about \( D_4 \) specific to this particular example. All the same, the method shows the program of the proof, which Cauchy breaks into three parts, as follows.
It is shown that if one assumes \( R < p \), then each value of K may not be changed by any substitution of degree p.

Partition the substitutions into blocks as suggested here, each containing \( M \) substitutions. By hypothesis, there are fewer than \( p \) blocks. Let \( Q = \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \) be a substitution of degree \( p \), where \( p \) is a prime number — he writes "degree" (degré) rather than order. Cauchy goes to some length to develop an algebra of substitutions; if \( A_1 \) and \( A_2 \) are permutations in his sense (rearrangements of the indices), then \( \Large \bigl(\begin{smallmatrix} A_1 \\ A_2 \end{smallmatrix}\bigr) \) is the substitution transforming \( A_1 \) into \( A_2 \). The word substitution continued to be used in his sense throughout the 19th century. Substitutions can be multiplied by one another and their powers taken, including the zeroth; there is an identity substitution and a substitution's period is the smallest whole number such that the substitution taken to that power is the identity substitution. He says that if \( A \) is a permutation, you can multiply it repeatedly by a given substitution and eventually the series will cycle back to the original permutation after \( p \) iterations, say, where \( p \) is the degree of the repeatedly applied substitution.
Imagine circles or regular polygons like those pictured below, where you start with each of the \( N \) permutations at the top, then apply \( Q \) to it repeatedly and array them around the polygon in a clockwise fashion until after \( p \) iterations you return to the starting point.
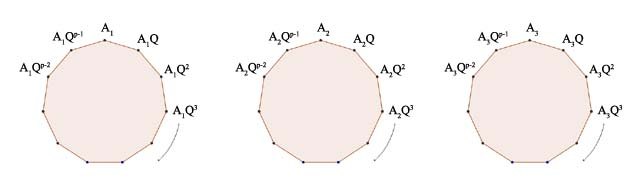
Ostensibly there are \( N \) polygons, one for each permutation, but in fact there are only \( N / p \) of them. To see this, suppose:
\[ \begin{align*}
{A_1 Q^u} &= {A_2 Q^v} \\
\therefore A_1 &= A_2 Q^v Q^{p-u} \\
&= A_2 Q^w, \hspace{16pt} 0 \leq w < p .
\end{align*} \]
That is, \( A_1 \) is in the polygon generated by \( A_2 \), and that is the general rule — any overlap implies complete overlap. That is to say, the polygons too partition the set of all permutations. Cauchy is using the fact that in these little cyclic subgroups, further multiplying an element by \( Q \) takes you eventually back to the identity; there are inverses! All the permutations in the first block are equivalent, meaning they lead to the same value \( K_1 \) of \( K \). Distributing them all among the polygons results in an least one polygon containing two of these equivalent permutations because there are more permutations in the first block of equivalent permutations (\( M \)) than there are polygons (\( N / p \)).
One of these substitutions is \( Q^r \) times the other one, meaning that applying \( Q \ r \) times doesn't change value \( K_1 \), but because \( p \) is prime, it is also true that some power of \( Q^r \) is \( Q \) itself, and since applying \( Q^r \) repeatedly doesn't change \( K_1 \), neither does applying \( Q \) itself. What's true of the first block is true of of all the others by the same analysis. QED Part 1.
It is shown that if a value of \( K \) cannot be changed by any substitution of degree \( p \), then it cannot be changed by any circular substitution of the 3rd degree.
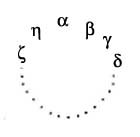
Cauchy talks at length about circular substitutions (substitution circulaire) just as we would, including this nice diagram suggesting letter substitutions around the circle and returning to the starting place: \( \alpha \to \beta \to \gamma \to \cdots \to \eta \to \alpha \). He relies on the fact that if \( p \) is prime, then all non-identity substitutions on \( p \) letters are circular of degree \( p \), so it is possible to write every three-cycle (substitutions circulaires du 3rd degré) as a product of substitutions of degree \( p \). Following is the notation and argument straight from the Memoire. Given any third degree substitution as shown on the right, compose two substitutions of degree \( p \) as follows on the left:
\[ \begin{pmatrix}
\color{red}{\alpha \ \beta \ \gamma} \ \delta \ \cdots \ \zeta \ \eta \\
\beta \ \gamma \ \delta \ \epsilon \cdots \ \eta \ \alpha
\end{pmatrix}
\begin{pmatrix}
\beta \ \gamma \ \delta \ \epsilon \ \cdots \ \eta \ \alpha \\
\color{red}{\gamma \ \alpha \ \beta} \ \delta \ \cdots \ \zeta \ \eta
\end{pmatrix} =
\begin{pmatrix}
\alpha \ \beta \ \gamma \ \delta \ \cdots \ \zeta \ \eta \\
\gamma \ \alpha \ \beta \ \delta \ \cdots \ \zeta \ \eta
\end{pmatrix} =
\begin{pmatrix}
\alpha \ \beta \ \gamma \\
\gamma \ \alpha \ \beta
\end{pmatrix} . \]
The indices other than \( \alpha, \beta, \gamma \) are cooked up to fill out the substitutions such that those parts reverse each other when the two substitutions of degree \( p \) are applied successively. Therefore if substitutions of degree \( p \) don't change the value \( K_1 \) of the function \( K \), then neither will any circular substitution of the third degree. QED Part 2.
It is shown that if a value of \( K \) is not changed by any circular substitution of third degree, then either this function is symmetric or else it has only two values.
A circular substitution of third degree can be written as the product (produit) of two transpositions:
\[ \begin{pmatrix}
\alpha \ \beta \ \gamma \\
\gamma \ \alpha \ \beta
\end{pmatrix} = (\alpha \ \beta) (\beta \ \gamma). \]
Since the substitution on the left doesn't change \( K_1 \), then the two transpositions applied in succession don't either. Conceivably \( (\alpha \ \beta) \) changes \( K_1 \) to some other value \( K_2 \), but then \( (\beta \ \gamma) \) must change \( K_2 \) back to \( K_1 \). In the latter situation, incidentally, \( (\alpha \ \beta) \) reciprocally changes \( K_2 \) to \( K_1 \) and \( (\beta \ \gamma) \) changes \( K_1 \) to \( K_2 \). In Similar vein:
\[ \begin{pmatrix}
\beta \ \gamma \ \delta \\
\delta \ \beta \ \gamma
\end{pmatrix} = (\beta \ \gamma) (\gamma \ \delta). \]
So each of those transpositions either leaves \( K_1 \) unchanged or changes it to some other value. But if \( (\beta \ \gamma) \) changes \(K_1 \) to some other value, then that value is \( K_2 \) from the discussion just before. It follows that \( K \) takes either one or two values; in the former case, the function is symmetric by definition. QED Part 3 and main theorem.
To recap the three parts of the proof and the main theorem following from them:
1) If the number of values taken by \( K \) is less than \( p \), then no substitution of degree \( p \) changes \( K \).
2) If \( K \) cannot be changed by any substitution of degree \( p \), then it cannot be changed by any circular substitution of degree 3.
3) If \( K \) cannot be changed by any circular substitution of degree 3, then the function is either symmetric or takes only two values.
Theorem: The number of different values of a non-symmetric function of n variables cannot be less than the largest prime number p contained in n without becoming equal to 2.
| Order | Index | #SG |
|---|---|---|
| 120 | 1 | 1 |
| 60 | 2 | 1 |
| 24 | 5 | 5 |
| 20 | 6 | 6 |
| 12 | 10 | 15 |
| Subgroups of \( S_5 \) with order \( \geq 12 \), #SG = # of each | ||
Cauchy gives this function as one of index \( 2 \) for a given \( n \):
\[ (x_1 - x_2)(x_1 - x_3) \cdots (x_1 - x_n)(x_2 - x_3) \cdots (x_2 - x_n) \cdots (x_{n-1} - x_n), \]
explaining how it produces exactly two values. Of course that generates \( A_n \), the alternating group of order \( n \), which is exactly half as large as its symmetric group. The main theorem above proves that \( S_5 \) has no subgroups of index \( 3 \) or \( 4 \); ie., of order \( 40 \) or \( 30 \), as born out by the list on the right from groupprops. To this day, \( S_5 \) is called the symmetric group of degree 5, no doubt a holdover from times past when this group was intimately connected with fifth degree algebraic functions.
Later in the memoir, Cauchy takes up the case of \( S_6 \) whose largest prime is also \( p = 5 \). Here too, the main theorem shows there cannot be subgroups of index \( 3 \) or \( 4 \) and since the order of \( S_6 \) is \( 720 \), that means there can be no subgroups of \( S_6 \) of order \( 240 \) or \( 180 \). Here \( p = 5 < n = 6 \) and he investigates whether there can be a subgroup of index \( 5 \), that is, order \( 144 \). He proves that there is not, saying he doesn't know of any \( n > 6 \) having an index less than \( n \), other than two, as mentioned above. In 1845, Bertrand proved that this is indeed the case, strengthening the main theorem. In the course of investigating \( S_6 \), Cauchy represents substitutions as the product of either an even or an odd number of transpositions, assuming implicitly that the evenness or oddness is invariant, a fact which has figured prominently ever since.
What amounts to the quadratic formula was known in antiquity and Scipione dal Ferro solved the cubic in 1515, exactly five hundred years ago and three hundred years before this memoir of Cauchy's. Solving a polynomial with integer coefficients means finding an expression for the roots in terms of the equation's coefficients using only addition, subtraction, multiplication, division, and root-taking. Then Cardan published the solution for the quartic (fourth degree) in Ars Magna in 1545. And there it sat for centuries, the quintic (fifth degree) resisting all attempts. And there were attempts — that is the context for Vandermode, Lagrange, and Ruffini's work. Lagrange analysed the old solutions for the cubic and quartic and introduced the reduced or resolvent equations they spawn that are solvable and in turn lead to solutions of the original equation. The resolvents involve permutations of the roots.
That's where Cauchy comes in and why he framed his permutation studies as he did. That \( S_5 \) does not contain subgroups of index \( 3 \) or \( 4 \) was highly significant, because it showed that the quintic wasn't amenable to the same methods as the cubic and quartic and tended to confirm the suspicion that the quintic was unsolvable in general, a fact proven by Abel in 1824 and giving this memoir of Cauchy's as the only citation. Galois digested and cited Cauchy's paper too, as noted by Professor Neumann in his recent impressive reconstruction of Galois's work (in time for the bicentennial of Galois's birth in 2011).[3]
So the motivation was firmly grounded in the desire to solve a nagging, longstanding problem arising from the history of the subject and a concrete, ongoing preoccupation of its practitioners. What's striking in retrospect is that not only was that problem put to bed, but the techniques developed for this express purpose were so fruitful, leading to the construction of vast empires of mathematics, of which classical Galois theory is only one example. By 1872, Felix Klein was pointing to group theory as the central organizing principle of geometry (the Erlangen Program) and number theory contributed another current to the great stream, but these origins in permutation theory were early and durable. Cauchy himself wrote extensively on the subject again in 1844 and 1845, further generalizing his work on permutation theory and proving among other things what is known today as Cauchy's Theorem, that if prime \( p \) divides the order of a group \( G \), then \( G \) has an element of order \( p \), a precursor of Sylow's first theorem, or as Eugen Netto called it, the Cauchy-Sylow Theorem.

Jordan's Traité des substitutions et des équations algébriques in 1870 is the first book on group theory and made a deep impression; it is based on his earlier work in this area and indeed on his thesis. Eugen Netto's Substitutionentheorie und ihre Anwendung auf die Algebra of 1882 had an impact as well, especially in the United States, where it was translated into English[4]. Netto was a student and follower of Kronecker, whose influence he was glad to acknowledge. The continuation of the earlier tradition is obvious even in the titles. Netto includes these theorems from Cauchy and his predecessors in §42, for example:
Theorem II. The order \( r \) of a group \( G \) of \( n \) elements is a divisor of \( n! \).
Theorem III. The number \( \rho \) of values of an integral function of \( n \) elements is a divisor of \( n! \).
Theorem IV. The product of the number \( \rho \) of the values of an integral function by the order \( r \) of the corresponding group is equal to \( n \).
The phrase group \( G \) of \( n \) elements might be confusing to a modern reader (we would say subgroup of \( S_n \)), but it's pretty recognizable, particularly the emphasis on the group and the use of the word, Galois's old term (gruppe in the original). In §114, he states and proves Bertrand's generalization of Cauchy's main result from 1815:
Theorem II. If the number \( \rho \) of the values of a function is less than \( n \), then either \( \rho = 1 \) or \( \rho = 2 \), and the group of the function is either symmetric or alternating. An exception occurs only for \( n = 4, \ \rho = 3, \ r = 8 \), the corresponding group being that belonging to \( x_1 x_2 + x_3 x_4 \).
As Netto continues, he starts to leave substitutions behind and takes up Kronecker's rational domains (fields), the adjunction of roots, and so on — you can almost feel the current pulling you towards modern Galois theory.
Mike Bertrand
December 14, 2014
^ 1. Memoire Sur le Nombre des Valeurs qu'une Fonction peut acquerir, lorsqu'on y permute de toutes les manieres possibles les quantites qu'elle renferme (Memoir on the number of values that a function can acquire when the variables it contains are permuted in all possible ways), by A. L. Cauchy, Journal de l'École polytechnique, Tome X, January 1815 (p 1-28). English translation.
^ 2. The Genesis of the Abstract Group Concept, by Hans Wussing (The MIT Press, 1984), ISBN 0-262-23109-3). Originally published in 1969 in the GDR as Die Genesis des Abstrakten Gruppenbegriffes. Ruffini's work is discussed on pp. 80-84.
^ 3. The Mathematical Writings of Évariste Galois, by Peter M. Neumann (European Mathematical Society, 2011), ISBN 978-3-03719-104-0. Galois's citation of Cauchy is discussed on p. 6 and shown in Galois's words on p. 128.
^ 4. The Theory of Substitutions and its Applications to Algebra, by Eugen Netto (The Register Publishing Company, 1892), translated by F. N. Cole.