CORDIC in C and Javascript
CORDIC is is a complex of fast algorithms to calculate transcendental functions using only table lookup, addition and bit shifting. Here I take up Volder's original scheme from 1959 to calculate sines and cosines quickly (CORDIC stands for COordinate Rotation DIgital Computer). My original article from 1992 holds up reasonably well, The CORDIC Method for Faster sin and cos Calculations, except for the Borland graphics — nice pre-Windows, but long-gone. Converting to Visual C requires only one change to the core routines related to moving from 16-bit to 32-bit integers (see comment in code). I've bundled up the source files for anyone who wants to take them into a Visual C Win 32 application, and here is a minimal C implementation. Wikipedia has a first-class article on this subject with lucid explanations and many pertinent references. Volder himself published an illuminating retrospective in 2000, explaining that the initial motivation was digitizing the navigation system of Convair's B-58 jet bomber (Volder worked for Convair).
Here is a minimal Javascript implementation, Javascript code here. The more extensive Javascript application on the right with rotating polygons is a proof of concept. Use the buttons along the bottom:
- Buttons at bottom-left for Play and Pause.
- Buttons at bottom-right to go faster or slower.
- Buttons in between for more sides or fewer sides.
This shows that:
a) The sines and cosines are accurate enough for many graphics applications (this one anyway!).
b) The sines and cosines are fast enough for such real-time purposes.
And these two points are the key ones: the trig ratios can be produced quickly and accurately enough for many applications. We are well-past the severely limited digital computers of the 1950s, so many of those applications are passé, but there are still situations where the hardware is limited (calculators, for example) and such integer-based routines are invaluable.
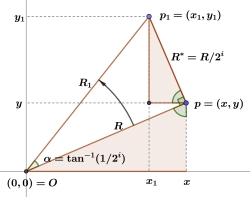
CORDIC generates sines and cosines by a series of successive approximations illustrated in this diagram. Suppose point \( p = (x, y) \) represents an initial approximation, with \( \cos = x /R \) and \( \sin = y /R \). Then swing vector \( R \) by angle \( \alpha = \tan^{-1}(1/2^i) \) in a counter-clockwise direction to vector \( R_1 \), locating point \( p_1 = (x_1, y_1) \) on \( R_1 \) perpendicular to \( R. \) \( \bigtriangleup Opp_1 \) is magnified here for the sake of understanding; it is in fact quite a small sliver, and all the smaller as \( i \) increases. The two colored right triangles are similar; to see this, note that the two marked acute angles at \( p \) are equal, both being complementary to the small sliver of white angle between them. \( \bigtriangleup Opp_1 \) is a right triangle by construction, whose acute angle at the origin is \( \tan^{-1}(1/2^i), \) also by construction. So if \( \alpha = \tan^{-1}(1/2^i) \) is the amount of the counter-clockwise swing, the white angle marked at the origin, then:
\[ \tan(\alpha) = {1 \over 2^i} = {R^* \over R}. \]
That is, the higher colored triangle is smaller than the lower colored triangle by a factor of \( 2^i. \) Note that \( R_1 \) is a little longer than \( R: \)
\[ R_1^2 = {R^2 + R^{*2}} = {R^2 + {R^2 \over 2^{2i}}} = {R^2\left(1 + {1 \over 2^{2i}}\right)}. \]
\begin{equation}{\therefore R_1 = R \cdot \sqrt{1 + {1 \over 2^{2i}}}.}\tag{1} \end{equation}
Now:
\[ y_1 = y + \underbrace{(y_1 - y),}_{\large \text{ leg of } R^* \text{ triangle }} \]
where \( y_1 - y \) is the longer leg of the \( R^* \) triangle, the higher colored one, and since that triangle is similar to the lower colored one and smaller than it by a factor of \( 2^i, \) we can relate the longer legs of the two triangles:
\[ y_1 - y = {x \over 2^i}. \]
Combining these two facts:
\begin{equation}{y_1 = y + {x \over 2^i}.}\tag{2} \end{equation}
and similarly:
\begin{equation}{x_1 = x - {y \over 2^i}.}\tag{3} \end{equation}
A similar diagram would show that swinging the original vector clockwise instead of counter-clockwise results in:
\begin{equation}{y_1 = y - {x \over 2^i}.}\tag{4} \end{equation}
\begin{equation}{x_1 = x + {y \over 2^i}.}\tag{5} \end{equation}
Equations (2-5) would put us in good shape if \( x \) and \( y \) were integers because not only are integer addition and subtraction fast for a computer, but so is division by a power of \( 2 \), amounting to shifting bits, one of the fastest operations a digital computer can execute.
To appreciate this, look at the calculation \( 45678 / 100, \) considered base ten in the usual way. As long as the remainder is not considered, the quotient can be obtained by simply shifting the digits of \( 45678 \) two places to the right, the \( 8 \) and then the \( 7 \) disappearing: \( 45678 \rightarrow 4567 \rightarrow 456. \) Each of those arrows represents a division by \( 10 \) with remainder ignored. Rounding can be effected by adding \( 50 \) (that is, half the denominator) to the the numerator before shifting: \( (45678 + 50) = 45728 \rightarrow 4572 \rightarrow 457. \)
For a base two example, consider \( 45 / 4 = 101101_2 / 10_2. \) As with base ten, shift the digits of the numerator to the right twice to obtain the quotient: \( 101101_2 \rightarrow 10110_2 \rightarrow 1011_2, \) this last being \( 11_{10}, \) the correct quotient ignoring the remainder. One way to think about this is that each digit in the shifted value represents one quarter as much as it did before shifting, so that will be true of the entire shifted number as well. Here is how to right-shift the bits of an integer in C:
#include "stdio.h"
void main()
{
int u, v;
u = 45;
// Shift the bits of u two places to the right.
v = u >> 2;
// Output: v = 11
printf("v = %d\n", v);
}
Everything in sight will be turned into an integer in order to facilitate fast calculations. Think of angle units: breaking the circle into 360 parts is just a historical accident, there's no reason it couldn't be divided into \( 2^{16} = 65,536 \) parts, and that is exactly what I'm going to do. There is nothing particularly magical about this choice, other than it being a power of two for fast calculating — it indicates the number of iterations that will be executed to find a sin / cos pair and the precision of the result. I'm going to call the new units CORDIC Angle Units (cau), where:
\[ 1^{\circ} = {{65,536 \text{ cau }} \over {360^{\circ}}} \sim 182 \text{ cau}. \]
Trig ratios too are stored as integers, thought of as a fraction of \( 2^{14} = 16,384, \) plus or minus. I call these values CORDIC Ratio Units (cru). \( 5000 \text{ cru}, \) for example, would represent the ratio:
\[ 5000 \text{ cru } = {5000 \over 16,384} = 0.3052. \]
Consider the following table to get a grip on these units:
\begin{array}{l|l|l|l|cr}
\text{angle}_{\text{deg}} & \text{angle}_{\text{cordic}} & \hskip{18pt} \text{sin}_{\text{cordic}} & \hskip{5pt} \text{sin}_{\text{lib}} & \text{error}\\[6pt]
\hline
\;\; 10^{\circ} & 1820 \text{ cau} & 2847 = 0.17377 & 0.17365 & +0.00012\\[4pt]
\;\; 20^{\circ} & 3641 \text{ cau} & 5605 = 0.34210 & 0.34202 & +0.00008\\[4pt]
\;\; 30^{\circ} & 5461 \text{ cau} & 8191 = 0.49994 & 0.50000 & -0.00006\\[4pt]
\;\; 40^{\circ} & 7282 \text{ cau} & 10531 = 0.64276 & 0.64279 & -0.00003
\end{array}
Let's walk through the first row for \( 10^{\circ}, \) that is, \( 10 / 360^{\text{th}} \) of a circle. The CORDIC equivalent is:
\[ 10^{\circ} \equiv {10 \over 360} \cdot 65,536 \text{ cau} = 1820 \text{ cau}, \]
the last calculation being rounded down. The algorithm produces \( 2847 \) for the CORDIC sine of this angle (the middle column), which also needs to be scaled:
\[ \text{sin}_{\text{cordic}}(2847) \equiv {2847 \over 16,384} = 0.17377. \]
Compare to the actual, or library, value \( \text{sin}_{\text{lib}}(10^{\circ}) = 0.17365 \) to see that the CORDIC value is too large by \( 0.00012. \)
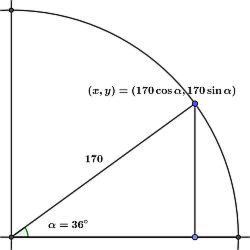
Suppose we want to calculate a vertex of a regular decagon. The central angle is one tenth of a circle:
\[ \alpha = 36^{\circ} = {{65,536 \over 10} \text{ cau }} = 6554 \text{ cau}. \]
The program calculates that:
\begin{align*}
\cos(6554 \text{ cau}) &= 13257,\\
\sin(6554 \text{ cau}) &= 9627,
\end{align*}
which compares with the actual values as follows:
\begin{alignat}{2}
{13,257 \over 16,384} &= 0.80914 \hspace{20pt} {9627 \over 16,384} &&= 0.58759\\
\cos 36^{\circ} &= 0.80902 \hspace{20pt} \sin 36^{\circ} &&= 0.58779
\end{alignat}
If the decagon is inscribed in a circle of radius \( 170, \) then the key calculations to find a vertex are:
\begin{alignat}{2}
x &= {170 \cdot \cos \alpha} &&= {170 \cdot {13,257 \over 16,384}} = {2,253,690 \over 16,384} = 137\\
y &= {170 \cdot \sin \alpha} &&= {170 \cdot {9627 \over 16,384}} = {1,636,590 \over 16,384} = 99
\end{alignat}
As suggested, the multiplication is performed first, then the division is effected by right-shifting bits. That is, the division is replaced by a faster multiplication, the shift being negligible. Furthermore, it is integer rather than floating point multiplication. Everything is rounded down here — the \( x \) and \( y \) values are really closer to \( 138 \) and \( 100. \) The correct values are obtained by adding \( 8192, \) half the denominator, to the numerators before shifting.
CORDIC works by successively approximating the given angle by the special angles \( \left\{\tan^{-1}(1/2^i)\right\}_{i=0}: \)
\begin{alignat}{3}
&\tan^{-1}(1) &&= 45^{\circ} &&&= 8192 \text{ cau}\\
&\tan^{-1}(1/2) &&= 26.57^{\circ} &&&= 4836 \text{ cau}\\
&\tan^{-1}(1/4) &&= 14.04^{\circ} &&&= 2555 \text{ cau}\\
&\tan^{-1}(1/8) &&= 7.13^{\circ} &&&= 1297 \text{ cau}\\
&\tan^{-1}(1/16) &&= 3.58^{\circ} &&&= 651 \text{ cau}\\
&&\vdots
\end{alignat}
The given angle can be taken in the first quadrant considering the symmetry of the situation. Using these special angles, \( 54^{\circ}, \) for example, is represented to a finer and finer precision as follows:
\begin{alignat}{2}
54^{\circ} &\sim 45^{\circ} &&= 45^{\circ}\\
54^{\circ} &\sim 45^{\circ} + 26.57^{\circ} &&= 71.57^{\circ}\\
54^{\circ} &\sim 45^{\circ} + 26.57^{\circ} - 14.04^{\circ} &&= 57.53^{\circ}\\
54^{\circ} &\sim 45^{\circ} + 26.57^{\circ} - 14.04^{\circ} - 7.13^{\circ} &&= 50.40^{\circ}\\
54^{\circ} &\sim 45^{\circ} + 26.57^{\circ} - 14.04^{\circ} - 7.13^{\circ} + 3.58^{\circ} &&= 53.98^{\circ}\\
&\vdots
\end{alignat}

This approximation has a physical interpretation. Think in terms of a vector \( 16384 \) units long and emanating from the origin in a standard \( x-y \) coordinate system. Starting at \( 0^{\circ} \) along the positive \( x \) axis, the vector rotates through each of the special angles one step at a time. Rotation at each step may be clockwise or counter-clockwise, whichever is needed to bring the vector closer to \( 54^{\circ}. \) The special angles represent rotations by smaller and smaller amounts, with positive signifying counter-clockwise rotation and negative signifying clockwise rotation.
Starting at \( 0^{\circ} \) along the positive \( x \) axis, plus \( 45^{\circ} \) is a counter-clockwise rotation into the middle of the first quadrant. The next step again rotates counter-clockwise by another \( 26.57^{\circ} \), but this results in \( 71.57^{\circ}, \) which overshoots the mark. The third rotation is therefore clockwise, signified by the minus \( 14.04^{\circ}, \) bringing the result back to \( 57.53^{\circ}. \) This continues as many times as there are bits in \( 16384 \) — \( 14 \) times. As mentioned above, rotating the vector results in a slight expansion at each step. The \( x \) and \( y \) coordinates of the rotating vector are the cosine and sine of the vector's angle at each step, after adjusting by the expansion factor, so each step of the iteration comes closer to \( \cos(54^{\circ}) \) and \( \sin(54^{\circ}). \)
Equation (1) gives the expansion of the rotating vector at each iteration. The effect accumulates, but is negligible in later iterations. The first rotation (\(45^{\circ}\)) expands the vector by a factor of \( \sqrt{2} = 1.414, \) the second rotation (\(26.57^{\circ}\)) expands it further by a factor of \( \sqrt{5/4} = 1.118, \) the third rotation (\(14.04^{\circ}\)) expands it again by \( \sqrt{17/16} = 1.031, \) and so on. The total expansion after fourteen iterations is:
\begin{align*}
\prod_{i=0}^{13} \sqrt{1 + {1 \over 2^{2i}}} &= \sqrt{\prod_{i=0}^{13} \left(1 + {1 \over 2^{2i}}\right)}\\
&= \sqrt{{2 \over 1} \cdot {5 \over 4} \cdot {17 \over 16} \cdot {65 \over 64} \cdot {257 \over 256} \cdots}\\
&= 1.646760.
\end{align*}
One approach (the one I take) is to divide the base of CORDIC Ratio Units, \( 2^{14} = 16,384, \) by this last figure before starting in order to offset the total expansion:
\[ \text{start with } {16,384 \over 1.646760} = 9949. \]
\( 9949 \) can be hard-coded if implementing on an embedded device without floating point math.
I'm executing on a computer, so have felt free to calculate the \( \tan^{-1} \)s with built-in trig routines; that won't subvert the main purpose of calculating many sines and cosines quickly, because those special angles are only calculated once in a CORDIC setup routine. The angles can be hard-coded on a device without trig.
Accuracy for this sixteen bit implementation averages to within about \( 0.0001, \) which gives perfect results when dealing with pixels in the range of hundreds, as in the decagon example above. One nice thing about this algorithm is that you can adjust the accuracy by changing the number of bits in the integer units, using long ints if necessary. There will be many applications where better accuracy is needed (consider that the C library routines are accurate to the precision of a C double, an eight-byte floating point value with a \( 52 \) bit mantissa, namely, about \( 15 \) decimal digits).
I was unpleasantly surprised to see that my CORDIC sines and cosines are four times slower than the built-in C library functions on my computer, but I shouldn't have been. Modern computers (writing in \( 2018 \)) have floating point and no doubt trig routines built in to the CPU, and they may use CORDIC routines for all I know (a version of CORDIC was used to calculate all the transcendental functions on the Intel 8087 math coprocessor, by the way — see the article by Rafi Nave in the references at the bottom). Things were different in the \( 1980 \)s, when floating point was implemented in software unless you had a math co-processor. You may have needed a million moderately accurate cosines per second for, say, ray-tracing applications. In such a situation, CORDIC was a tenable approach.
CORDIC was implemented on calculators from early days. The case for Hewlett Packard is particularly well documented, with lead designer David C. Cochran writing about it at the time for the revolutionary HP-35 scientific calculator introduced in 1972. Don't deny yourself the pleasure of listening to this brilliant engineer in the YouTube on the right — Here is Cochran in 2010:
The choice of algorithms for the HP-35 received considerable thought. Power series, polynomial expansions, continued fractions, and Chebyshev polynomials were all considered for the transcendental functions. All were too slow because of the number of multiplications and divisions required to maintain full ten-digit accuracy over the proposed two-hundred decade range. The generalized algorithm that best suited the requirements of speed and programming efficiency for the HP-35 was an iterative pseudo-division and pseudo-multiplication method described in 1624 by Henry Briggs in 'Arithmetica Logarithmica' and later by Volder and Meggitt. This is the same type of algorithm that was used in previous HP desktop calculators.
The "iterative pseudo-division and pseudo-multiplication method" is of course CORDIC and adaptations of the same basic method were used to calculate other transcendental functions (in 1962, Meggitt had published an article in an IBM journal showing how such algorithms can calculate logs, square roots, and even quotients). The reference to Henry Briggs in 1624 is amusing as well as instructive, warning off would-be litigators who might want to yammer about prior art. In 1971, J. S. Walther of HP revealed a single unified CORDIC-like iterative algorithm for calculating a range of elementary functions including division, sin, cos, tan, arctan, ln, and square root. An excellent reference on CORDIC trig and related algorithms for other transcendental functions was published in the Hewlett Packard Journal in 1977-78 by William E. Egbert.
Other calculators use CORDIC as well, notably those by Texas Instruments — this reference from some TI engineers says that "TI calculators have almost always used CORDIC".
Unlike my implementation of CORDIC, calculators typically represent numbers in binary-coded decimal (BCD) and execute internal algorithms accordingly. No matter, the idea is the same.

In his retrospective article in 2000, The Birth of CORDIC, Jack Volder writes of necessity being the mother of invention as his Convair team in Fort Worth attempted to digitize the navigation system on the B-58 bomber. He pondered the question like a sage of old, one imagines, describing his eureka moment like this:
I began looking for some clue to solving this problem in the trigonometric equations tabulated in my 1946 edition of the Handbook of Chemistry and Physics. This led to the massaging of the basic angle addition equations to obtain the following interesting equations. If \(\small \tan(\phi) = 2^{−n}, \) then: \begin{align*} \small K_n R \sin(\theta \pm \phi) &= \small R \sin(\theta) \pm 2^{-n} R \cos(\theta)\\ \small K_n R \cos(\theta \pm \phi) &= \small R \cos(\theta) \mp 2^{-n} R \sin(\theta) \end{align*} where \(\small K_n = \sqrt{1 + 2^{−2n}}. \)
He had to get permission from Convair and the Air Force to publish his results in 1959. It's a small marvel that both were so forthcoming, as was Hewlett Packard as they diffused the technology. One thinks of how the Internet too was a project of the U. S. military in concert with university researchers. The entanglement of new science and mathematics with productive technology is an old story, one nicely illustrated by CORDIC. It was the same in seventeenth century England, as Robert Merton sketched out in 1939, pointing to shipping and commerce, the military, and all manner of practical enterprise as the spur for technical and scientific innovation.
How beautiful is the entire integrated development. The basic geometry would have been appreciated by Greek mathematicians 2500 years ago, just as Henry Briggs would have liked the shifting strategies so similar to his approach to logarithms in 1624. Modern electronic technology is heavily implicated, CORDIC papers commonly showing the electronic circuits critical for engineers at the point of production. Who would have guessed that trig and binary math could be so closely connected, that an algorithm could be found to to calculate sines and cosines bit by bit. Plus, we can implement CORDIC in software on modern computers for instruction and to be transferred verbatim (or close) to small devices. All excellent!
Mike Bertrand
May 8, 2018
1) "Science and the Economy of Seventeenth Century England", by Robert K. Merton, Science & Society, Vol. 3, No. 1 (Winter, 1939), pp. 3-27.
2) "The CORDIC Computing Technique", by Jack Volder, Proceedings of the Western Joint Computer Conference , March 1959, pp. 257–261.
3) "The CORDIC Trigonometric Computing Technique", by Jack Volder, IRE Transactions on Electronic Computers 8, Sep 1959, pp. 226–230.
4) "Pseudo Division and Pseudo Multiplication Processes", by J. E. Meggitt, IBM Journal, April 1962 , pp. 210-226.
5) "A unified algorithm for elementary functions", by J. S. Walther, Proceedings of the Spring Joint Computer Conference 38, May 1971 pp. 379–385.
6) "Algorithms and Accuracy in the HP-35", by David C. Cochran, Hewlett Packard Journal 23, June 1972, pp. 10-11.
7) "Personal Calculator Algorithms I, II, III, IV", by William E. Egbert, Hewlett Packard Journal, May 1977 - April 1978.
8) "Implementation of Transcendental Functions on a Numerics Processor", by Rafi Nave, Microprocessing and Microprogramming 11, 1983, pp. 221-225.
9) Computer Arithmetic, vol 1, by Earl E. Swartzlander, Jr. (ed.), IEEE, 1990, ISBN 0-8186-8931-5. Contains many of the classic articles.
10) "The CORDIC Method for Faster sin and cos Calculations", by Michael Bertrand, The C Users Journal, Nov 1992, pp. 57-64.
11) "The Birth of CORDIC", by Jack E. Volder, Journal of VLSI Signal Processing 25, 2000, pp. 101–105.
12) "The HP-35 Design: A Case Study in Innovation", by David S. Cochran, Nov 2010.