Riesz Proves the Riesz Representation Theorem

Frigyes Riesz.

The Riesz Representation Theorem is a foundation stone of 20^th century functional analysis. Generalized almost beyond recognition, Frigyes (Frédéric) Riesz originally proved the theorem in 1909 for \( C[0,1] \), the continuous real-valued functions on \( [0,1] \):

If \( \mathcal{A} \) is a bounded linear functional on \( C[0,1] \), then there is a function \( \alpha \) of bounded variation on \( [0,1] \) such that for all \( f \in C[0,1] \): \[ \mathcal{A}[f(x)] = {\int_0^1 f(x)d\alpha(x).} \hskip{60pt} (1) \]

In this article, I propose to retrace Riesz's original proof in Sur les opérations fonctionnelles linéaires^[1] in 1909, augmenting with his discussion in Sur certains systèmes singuliers d'équations intégrales^[2] in 1911 where appropriate.

Fonctionnelles linéaires in 1909 is the original three page announcement — compact to a fault, and challenging, if illuminating, to fill in. Details followed in Équations intégrales in 1911, the first three sections of which concern the proof.

Riesz considers distributive and continuous operations \( \mathcal{A} \) from \( C[0,1] \) to \( \mathbb{R} \), which he denominates linear (Une opération distributive et continue est dite linéaire), functionals in modern parlance. Such an operation is continuous if when \( f_n \) are continuous functions on \( C[0,1] \) such that \( f_n \rightarrow f \), then \( \mathcal{A}(f_n) \rightarrow \mathcal{A}(f) \). He doesn't define distributive, but the context (and all later discussion, including his own) makes clear that he means:

\[ {\mathcal{A}(f + g) = \mathcal{A}(f) + \mathcal{A}(g)}, \hskip{20px} {\mathcal{A}(af) = a \cdot \mathcal{A}(f)}, \hskip{20px} \text{ where } f, g \in C[0, 1], \hskip{10px} a \in \mathbb{R}. \]

A real function \( f \) on \( [0,1] \) is said to be of bounded variation if the quantity

\[ \begin{equation}{{\sum_{k=0}^{n-1}|f(x_{k+1})-f(x_k)|}} \tag{2} \end{equation} \]

is bounded for all partitions \( \{{0 = x_0} < x_1 < x_2 < \cdots < {x_n = 1}\} \) of \( [0,1] \). The supremum of (2) is called the total variation \( V(f) \) of \( f \). The function \( g(x) = x^2 \sin{(1/x)}, g(0) = 0 \) is of bounded variation on \( [0,1] \), for example, while \( h(x) = x \sin{(1/x)}, h(0) = 0 \) is not. For such continuous functions, think of traveling along the graph of the curve as \( x \rightarrow 0 \) and add up the \( y \) increments in the course of the traversal — that is the total variation in the limit and it is finite for \( g \) but not for \( h \). If \( f \) is differentiable and its derivative is Riemann-integrable, the sum of those \( y \) increments, in the limit, is just the vertical component of the arc-length of its graph:

\[ V(f) = {\int_a^b |f'(x)| dx.} \]

The integral on the right side of (1) was introduced by Stieltjes in 1894, though Riesz wrote that Gyula Kőnig told him he had used it before that. It's now known as the Riemann–Stieltjes integral and is defined by Riesz like this:

Let us briefly recall the meaning of this expression (the integral on the right side of (1)). We understand the limit of the sum \( \sum_i f(\xi_i)[\alpha(x_{i+1}) - \alpha(x_i)] \) corresponding to a division of the interval (0, 1) into a finite number of subintervals; \( \xi_i \) denotes an element of the interval \( (x_i, x_ {i + i}) \). The passage to the limit is subject only to the sole condition that the length of the subintervals tends uniformly to zero.

Riesz says a distributive and continuous operation is bounded and proves it in §III of Équations intégrales, bounded here meaning there is a fixed value \( M_{\mathcal{A}} \), such that for all \( f \in C[0,1] \):

\[ \begin{equation}{|\mathcal{A}[f(x)]| \leq M_{\mathcal{A}} \times max. |f(x)|.} \tag{3} \end{equation} \]

He points out that

\[ {\left|\int_0^1 f(x)d\alpha(x)\right|} \leq \text{ maximum of } |f(x)| \times V(\alpha(x)), \]

when \( \alpha(x) \) is of bounded variation, showing that that \( {\mathcal{A}[f(x)]} = {\int_0^1 f(x)d\alpha(x)} \) is a linear operation (functional). He wants to show that every linear operation is of this form — that is the Riesz Representation Theorem on \( C[0,1] \).

He continues:

After these preliminaries, given a linear operation \( \mathcal{A}[f(x)] \), we define the function \( \text{A}(x) \) by the equality \( \text{A}(\xi) = \mathcal{A}[f(x;\xi)] \), where we designate by \( f(x;\xi) \) the function equal to \( x \) for \( 0 \leq x \leq \xi \) and to \( \xi \) for \( \xi \leq x \leq 1 \). Now by applying the inequality (3) to the continuous function \( f(x) \) defined by the conditions \( {f(x_i) = 0}; {f\left({{x_i+x_{i+1}} \over 2}\right)} = {\text{sign}[\text{A}(x_{i+i}) - \text{A}(x_i)]} \), \( f(x) \) is linear in each half-interval, and we get the inequality \[ \begin{equation}{ {{\LARGE{\sum_i}} {{\left|\text{A}(x_i)-2\text{A}\left({{x_i+x_{i+1}}\over 2}\right)+\text{A}(x_{i+1})\right|} \over {x_{i+1}-x_i}}} \leq {M_{\mathcal{A}} \over 2}.} \tag{4} \end{equation} \]

Let's dig in to this. Consider a partition \( \{{0 = x_0} < x_1 < x_2 < \cdots < {x_n = 1}\} \) of \( [0,1] \) and define \( f(x) \) on it as suggested in the image: \( f(x) = 0 \) at each partition point \( x_i \) and \( f(x) = \pm 1 \) midway between partition points, whether \( +1 \) or \( -1 \) to be determined. Within each subinterval, connect the three points to trace out a continuous piecewise linear function, so \( f(x) \) consists of a series of connected peaks above and below the \( x \) axis reaching up to \( y = 1 \) and down to \( y = -1 \), the seesaw figure pictured here (note the increments \( \delta_i = {x_{i+1} - x_i} \) are not necessarily equal).

Riesz says to go up to \( y = 1 \) in a subinterval \( (x_i, x_{i+1}) \) if:

\[ {\text{A}(x_{i+1}) - \text{A}(x_i)} = {\mathcal{A}[f(x;x_{i+1})] - \mathcal{A}[f(x;x_i)]} = {\mathcal{A}[f(x;x_{i+1}) - f(x;x_i)]} > 0, \]

and go down to \( y = -1 \) otherwise. That is, go up if the functional of \( f(x;x_{i+1}) - f(x;x_i) \), shown to the right, is greater than \( 0 \), go down otherwise. That's not right and is corrected in Équations intégrales, where he says the condition should be based directly on the numerator inside the sum of (4), namely, go down to \( -1 \) if and only if:

\[ \text{A}(x_i) -2\text{A}\left({{x_i + x_{i+1}} \over 2}\right) + \text{A}(x_{i+1}) < 0, \]

\[ \text{ie.,} \hskip{10pt} \mathcal{A}[f(x;x_i)] - 2 \mathcal{A}\left[f\left(x;{{x_i + x_{i+1}} \over 2}\right)\right] + \mathcal{A}[f(x;x_{i+1})] < 0, \]

\[ \text{or} \hskip{10pt} \mathcal{A}\left[f(x;x_i) - 2f\left(x;{{x_i + x_{i+1}} \over 2}\right) + f(x;x_{i+1})\right] < 0. \]

The function on the third line is pictured here for \( (x_1, x_2) \) and adding them all together results in a version of the sawtooth function \( f(x) \), but with each peak pulled towards the \(x\)-axis so that the peak angle is 90°, making an isosceles right triangle. So if \( \delta_i = {x_{i+1} - x_i} \), then the \( i^{th} \) peak is \( \delta_i / 2 \) above or below the \(x\)-axis, as the case may be.

To flesh this out, let \( P_i(x) \) be the piecewise linear peak function on \( (x_i, x_{i+1}) \), \( 0 \) elsewhere, so \( f(x) = {\sum_{i=0}^{n-1} P_i(x)} \). Then put \( S_i(x) = \) \( (\delta_i / 2) \cdot P_i(x) = \) \( f(x;x_i) - 2f\left(x;{{x_i + x_{i+1}} \over 2}\right) + f(x;x_{i+1}) \), pulling the peak down (or up) to the little isosceles triangle. Applying (3) to \( f(x) \):

\[ \mathcal{A}[f(x)] \leq {M_{\mathcal{A}} \cdot max |f(x)|} = {M_{\mathcal{A}} \cdot 1} = M_{\mathcal{A}}. \]

\[ \therefore {\mathcal{A}\left[\sum_{i=0}^{n-1} P_i(x)\right]} = {\sum_{i=0}^{n-1} \mathcal{A}[P_i(x)]} = {\sum_{i=0}^{n-1} \mathcal{A}\left[{S_i(x) \over {\delta_i/2}}\right]} \leq M_{\mathcal{A}}. \]

Pulling the \( \delta_i / 2 \) outside functional \( \mathcal{A} \) (it's linear!) and then the \(2 \) outside the sum leads to:

\[ {\sum_{i=0}^{n-1} \mathcal{A}\left[{S_i(x) \over \delta_i} \right]} = {\sum_{i=0}^{n-1} {{\mathcal{A}[{S_i(x)}]} \over \delta_i}} \leq {M_{\mathcal{A}} \over 2}. \]

That is:

\[ {{\LARGE{\sum_{\large{i=0}}^{\large{n-1}}}}{{\mathcal{A}[{f(x;x_i) - 2f\left(x;{{x_i + x_{i+1}} \over 2}\right) + f(x;x_{i+1})}]} \over \delta_i}} \leq {M_{\mathcal{A}} \over 2}. \]

This is Riesz's inequality (4) except for the absolute value signs, and they can be put in because \( f(x) \) and \( S(x) \) were chosen exactly so that they can.

Next he says, "It follows that the derived numbers of the function \( \text{A}(x) \) exist and that these derivatives are functions of bounded variation." The term derived number refers to a limit point of the difference quotients and Riesz is saying they are uniformly bounded throughout the interval. It's not perfectly clear, but helps to rewrite (4) as:

\[ \begin{equation}{{{\LARGE{\sum_{\large{k=1}}^{\large{m-1}}}} \left|{{\text{A}(x_{k+1}) - \text{A}(x_k)} \over {x_{k+1}-x_k}} - {{\text{A}(x_k) - \text{A}(x_{k-1})} \over {x_k-x_{k-1}}} \right|} \leq G,} \tag{5} \end{equation} \]

as Riesz himself does in Équations intégrales. Here \( x_k \) plays the role of the midpoint and the rearrangement as a sum of differences of difference quotients is highly suggestive. Putting \( D_k = \large{{\text{A}(x_k)-\text{A}(x_{k-1})} \over {x_k-x_{k-1}}} \), (5) reads:

\[ \begin{equation}{\sum_{k=1}^{m-1} |D_{k+1} - D_k| \leq G,} \tag{6} \end{equation} \]

so it's plain that the difference quotients are of bounded variation and therefore themselves bounded, much like any function of bounded variation is itself bounded (Riesz goes into this a bit in 1911). He says to put \( \alpha(x) \) equal to the negative of the upper right derivative (le nombre dérivé supérieur de droite) throughout \( (0,1) \), some special handling required at the endpoints (\( \alpha (0) = -\text{A}[n(x)] \), where \( n(x) \) is the function with the constant value \(1 \), \( \alpha (1) = 0\)). Today this is called a Dini derivative — there are four of them with the limit being taken from left or right in \( x \) and taking the greatest or smallest limit point (all four are equal for a differentiable function). The upper right Dini derivative Riesz appeals to is defined as:

\[ {D^+ \text{A}(x)} = {\limsup\limits_{h \rightarrow 0^+} {{\text{A}(x+h) - \text{A}(x)} \over h}}. \]

The boundedness of the difference quotients ensures that the upper Dini derivatives are finite — this is a key point. And because the difference quotients are of bounded variation, so are \( D^+ \text{A}(x) \) and \( \alpha(x) \).

Riesz takes it for granted that representation (1) holds for the base functions \( f(x;\xi) \) with the \( \alpha(x) \) he specified:

\[ \mathcal{A}[f(x;\xi)] = {\int_0^1 f(x;\xi) \; d\alpha(x)}. \]

Let's spell out why it does. The left side is \( \text{A}(\xi) \) by definition. We can break down the right side using the formula for integration by parts for Riemann-Stieltjes integrals, ascribed by Riesz directly to Stieltjes' 1894 paper in §II of Équations intégrales:

\[ {\int_a^b f(x) \; d\alpha(x) + \int_a^b \alpha(x) \; df(x)} = { f(b)\alpha(b) - f(a)\alpha(a)}. \]

Applying this formula to the integral from \( 0 \) to \( \xi \), with \( f(x) = x \), results in:

\[ \begin{align*}
{\int_0^1 f(x;\xi) \; d\alpha(x)} &= {\int_0^\xi x \; d\alpha(x)} + {\int_\xi^1 \xi \; d\alpha(x)} \\
&= \left( \xi \cdot \alpha(\xi) - 0 \cdot \alpha(0) - \int_0^\xi \alpha(x) \; dx \right) + {\int_\xi^1 \xi \; d\alpha(x)} \\
&= \Big(\xi \cdot \alpha(\xi) + (\text{A}(\xi) - \text{A}(0))\Big) + \xi \cdot (\alpha(1) - \alpha(\xi)).
\end{align*} \]

The two \( \xi \cdot \alpha(\xi) \) terms cancel each other out; \( \text{A}(0) \) is the functional evaluated at the function that is identically \( 0 \), which is \( 0 \) by the linearity of the functional; and \( \alpha(1) \) is \( 0 \) by definition. That is, everything on the third line drops out except \( \text{A}(\xi) \), proving that (1) holds for \( f(x;\xi) \), QED.

The tricky part of this little proof is ensuring that the indefinite integral of the Dini derivative is the function it is the derivative of, \( \text{A}(x) \), a routine enough maneuver for a function whose derivative is integrable. The master spells it out near the start of Équations intégrales, where he writes:

En réalité, la fonction \( \text{A}(x) \) admet des dérivées a gauche et à droite. Quant à notre but, il nous suffira de démontrer qu'elle admet l'un quelconque des quatre nombres dérivés, et que celui-ci représente une fonction à variation bornée. Car toute fonction à variation bornée est intégrable au sens de Riemann, et quand un nombre dérivé est intégrable, sa fonction primitive en est l'intégrale indéfinie(1).

In reality, the function \( \text{A}(x) \) has derivatives on the left and on the right. As for our purpose, it suffices to show that it admits any of the four derived numbers, and that they are functions of bounded variation. For every function of bounded variation is Riemann integrable, and when a derived number is integrable, its original function is the indefinite integral.

This passage has a footnote to Lebesgue's landmark 1904 treatise Leçons sur l'intégration et la recherche des fonctions primitives (Lessons on integration and the search for primitive functions), where these matters are addressed.

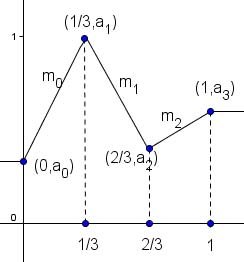
Given real values \( a_0, a_1, a_2, \cdots a_n \), we want to build a piecewise linear function on \( [0,1] \) with the abscissas evenly spaced and the ordinates the \( a_k \) — in other words, a piecewise linear function connecting \( (0,a_0), \; (1/n,a_1), \; (2/n,a_2), \cdots \) \( (1,a_n) \) as the corner points, as pictured here for \( n = 3 \). That function is:

\[ p(x) = a_0 + \sum_{k=0}^{n-1} m_k \cdot \Big(f(x;{{(k+1)} / n}) - f(x;{k / n})\Big), \]

where \( m_k = {{(a_{k+1} - a_k)} / {(1/n)}} \), that is, the slope of the line segment connecting \( (k/n,a_k) \) to \( ({(k+1)}/n,a_{k+1}) \).

It's evident that \( p(x) \) is piecewise linear because it is a linear combination of piecewise linear functions. Moreover, the corners occur exactly at the corners of its summand functions, namely, at \( j = 0, 1/n, \) \(2/n, \cdots 1 \). To see that \( p(j/n) = a_j \), proceed by induction on \( j \). For \( j = 0 \), \( x = {0 / n} = 0 \) and all the \( f(x; \xi) = 0 \), so \( p(0) = a_0 \). For \( j = 1 \):

\[ \begin{align*}
p(1/n) &= a_0 + m_0 \cdot {\big(f(1/n;1/n) - f(1/n;0)\big)} + \sum_{k=1}^{n-1} m_k \cdot \Big(f(1/n;{(k+1)} / n) - f(1/n;k / n)\Big) \\
&= a_0 + {{a_1-a_0} \over {1/n}} \cdot (1/n - 0) \\
&= a_0 + (a_1-a_0) \\
&= a_1.
\end{align*} \]

The sum on the first line vanishes because the two base function are equal for \( k \geq 1 \). The inductive step is much the same, with all the calculations up to the current point the same as in the earlier step, an adjustment involving the current slope, and the tail of the sum being \( 0 \). There is nothing critical about equal spacing on the \( x \) axis, by the way — the argument generalizes in a straightforward way.

The functional \( \mathcal{A} \) is linear and so is the Riemann-Stieltjes integral with respect to the integrand, so since (1) holds for the functions \( f(x;\xi) \), it also holds for linear combinations of them:

\[ \mathcal{A}[p(x)] = {\int_0^1 p(x) \; d\alpha(x),} \]

where \( p(x) \) is any piecewise linear function on \( [0,1] \).

The final proof follows from the fact that any continuous function on \( [0,1] \) is the uniform limit (limit in the sup norm) of piecewise linear functions by putting \( a_k = f(k/n) \):

\[ \begin{align*}
\mathcal{A}[f(x)] &= \mathcal{A}[{\displaystyle \lim_{n \rightarrow \infty}} p_n(x)] \\
&= {\displaystyle \lim_{n \rightarrow \infty}} \mathcal{A}[p_n(x)] \\
&= {\displaystyle \lim_{n \rightarrow \infty}} \int_0^1 p_n(x) \; d\alpha(x) \\
&= \int_0^1 f(x) \; d\alpha(x)
\end{align*} \]

The first line is because the \( p_n(x) \rightarrow f(x) \), the second line because functional \( \mathcal{A} \) is continuous, the third line because (1) holds for the \( f(x;\xi) \) and their linear combinations and the fourth line by a simple calculation based on the fact that \( p_n(x) \rightarrow f(x) \) uniformly in the sup norm. This completes the proof of (1) for all continuous functions \( f(x) \) on \( [0,1] \), the celebrated Riesz Representation Theorem:

\[ \mathcal{A}[f(x)] = {\int_0^1 f(x)d\alpha(x).} \]

This proof has many fine qualities, the foremost for me being that I can understand it, unlike the ten-step version encountered in Rudin^[4] all those years ago:

Let \( X \) be a locally compact Hausdorff space, and let \( \Lambda \) be a positive linear functional on \( C_c(X) \). Then there exists a \( \sigma \)-algebra \( \mathfrak{M} \) in \( X \) which contains all Borel sets in \( X \), and there exists a unique positive measure \( \mu \) on \( \mathfrak{M} \) which \( \cdots \)

It goes on. And on — half a page for the statement and six pages for the proof. Professor Rudin points out that there is good reason for generalizing here, namely, that Lebesgue measure can be constructed from functionals as the primitive concept. It's not that a functional is an integral, but that an integral is a functional, concepts of length and measure following from that (Rudin, p 34). Fine, but fifteen years before Rudin, Riesz's final proof of his Representation Theorem looked more like the foregoing than anything in Rudin. Instead of the \( f(x;\xi) \), he used simple discontinuous (characteristic) functions in 1952^[3], proving the version of the Hahn-Banach Theorem needed to extend the functional to a domain including simple characteristic functions.

There is something very attractive about proving such a general result based on these simple and concrete considerations. In his essay The Shaping of the Riesz Representation Theorem^[5], Jeremy Gray writes at length of Riesz's role as a skilled navigator between old and new and in particular of his effective leveraging of the Weierstrass Approximation Theorem as a fulcrum. Hadamard's precursor proof of 1903 was based on the kernel function \( e^{-x^2} \) Weierstrass used to prove his theorem in 1886. Riesz's proof, simpler but more general, followed Lebesgue's approach of approximating continuous functions by polygonal line segments (Sur l'approximation des fonctions, 1898).

O'Connor and Robertson's account of Riesz at St. Andrews includes this tribute by W. W. Rogosinski in his obituary in 1956:

The work of F Riesz is not only distinguished by the genuine importance of his results, but also by his aesthetic discernment in mathematical taste and diction. ... The more leisurely mastership of F Riesz's style, whether he writes in his native Hungarian, or in French or German, conveys such pleasure and is to the older mathematician a nostalgic reminder of what we are in danger to lose. For him there was no mere abstraction for the sake of a structure theory, and he was always turning back to the applications in some concrete and substantial situation.

Here (in his book Leçon's d'analyse fonctionnelle), in the first half written by himself, we find the old master picturing to us Real Analysis as he saw it, lovingly, leisurely, and with the discerning eye of an artist. This book, I have no doubt, will remain a classic in the treasure house of mathematical literature. With it, and with all his other work, will live the memory of Frederic Riesz as a great and fertile mathematician for long in the history of our art.

Frigyes Riesz was a great bridging figure, firmly rooted in the classical real analysis of the mid and late 19^th century, at the same time extending and generalizing the foundation with an unerring instinct for enduring mathematical value.

Mike Bertrand

May 24, 2015

^ 1. Sur les opérations fonctionnelles linéaires (On linear functional operations), by Frédéric Riesz, Comptes rendus, 149 (1909), p 974–977.

^ 2. Sur certains systèmes singuliers d'équations intégrales (On some noteworthy systems of integral equations), by Frédéric Riesz, Annales scientifiques de l'École Normale Supérieure, 28 (1911), p 33-62.

^ 3. Functional Analysis, by Frigyes Riesz and Béla Szőkefalvi-Nagy (Dover Publications, 1990), ISBN 0-486-66289-6. First published in English in 1955 as a translation of the 1952 original, Leçon's d'analyse fonctionnelle. See p. 106-110 for Riesz's last proof of his Representation Theorem.

^ 4. Real and Complex Analysis, by Walter Rudin (McGraw-Hill Book Company, 1966). See the Riesz Representation Theorem on p. 40-47.

^ 5. The Shaping of the Riesz Representation Theorem: A Chapter in the History of Analysis, by J. D. Gray, Archive for History in the Exact Sciences, 31(2), 1984–85, p. 127–187.