Pascal on Sums of Powers of Integers

Blaise Pascal (1623–1662)

Pascal's celebrated paper Traité du triangle arithmétique (Treatise on the Arithmetic Triangle)^[1] was written in 1654 and published in 1665. Though since named for him because of this work, "Pascal's" Triangle was long known in Europe before 1650 and in other civilizations too^[2]. The Traité contains a short appendix, Potestatum Numericarum Summa (The Sum of Powers of Numbers)^[3], showing how to derive polynomial expressions for sums of powers of integers like:
\begin{equation}{\sum_{k=1}^n k^2 = {1^2 + 2^2 + 3^2 + \cdots + n^2} = {{1 \over 6} n (n + 1)(2n+1)} = {{1 \over 3}n^3 + {1 \over 2}n^2 + {1 \over 6}n}.}\tag{1} \end{equation}

In Potestatum, Pascal walks through an extended example to exemplify his method, namely, finding:
\[ S = 5^3 + 8^3 + 11^3 + 14^3. \]
He says the method can be applied to the sum of any series of positive integers in arithmetic progression, each raised to the same positive integral power. Here the difference of the progression is \( 3 \) and the power is, coincidentally, also \( 3. \) The sum is easily calculated directly as \( S = 4712, \) but the point is to exemplify the method. Pascal says to introduce a variable \( A, \) then expand \( (A + 3)^4 \) by the binomial theorem, where \( 3 \) is the progression's difference and \( 4 \) is one more than the power:
\begin{align*}
(A + 3)^4 &= A^4 + 12 A^3 + 54 A^2 + 108 A + 81\\
\therefore (A + 3)^4 - A^4 &= 12 A^3 + 54 A^2 + 108 A + 81\\
\end{align*}
Plug in \( A = 14, A = 11, A = 8, A =5 \) successively to the second equation:
\begin{alignat*}{5}
17^4 &- 14^4 &&= 12 \cdot 14^3 &&+ 54 \cdot 14^2 &&+ 108 \cdot 14 &&+ 81\\
14^4 &- 11^4 &&= 12 \cdot 11^3 &&+ 54 \cdot 11^2 &&+ 108 \cdot 11 &&+ 81\\
11^4 &- 8^4 &&= 12 \cdot 8^3 &&+ 54 \cdot 8^2 &&+ 108 \cdot 8 &&+ 81\\
8^4 &- 5^4 &&= 12 \cdot 5^3 &&+ 54 \cdot 5^2 &&+ 108 \cdot 5 &&+ 81\\
\end{alignat*}
Adding these four equations leads to much cancellation on the left (this is the point!):
\[ 17^4 - 5^4 = 12 \cdot (\color{red}{14^3 + 11^3 + 8^3 + 5^3}) +54 \cdot (14^2 + 11^2 + 8^2 + 5^2) + 108 \cdot (14 + 11 + 8 + 5) + 4 \cdot 81. \]
We're seeking the sum in red, which can be solved for in this equation using standard algebraic techniques:
\begin{align}
83521 - 625 &= 12 \cdot (\color{red}{14^3 + 11^3 + 8^3 + 5^3}) + 54 \cdot 406 + 108 \cdot 38 + 4 \cdot 81\\
\therefore 83521 &= 12 \cdot (\color{red}{14^3 + 11^3 + 8^3 + 5^3}) + 21924 + 4104 + 324 + 625\\
&= 12 \cdot (\color{red}{14^3 + 11^3 + 8^3 + 5^3}) + 26977\\
\therefore \color{red}{14^3 + 11^3 + 8^3 + 5^3} &= (83521 - 26977) / 12\\
&= 4712.
\end{align}
On the face of it, this looks more involved and harder that the original calculation. But the beauty of it is to reduce a sum of cubes problem to a couple fourth powers, a sum of squares, and the sum of a simple arithmetic progression (first powers). Pascal points out that even ancient authors knew how do such calculations, so implicit in this example is a method for calculating sums of cubes. In a similar way, a sum of fourth powers can be reduced to a couple fifth powers, a sum of cubes, a sum of squares, and the sum of an arithmetic progression.

It's a small wonder how Pascal rolls out the calculations verbally with little recourse to algebraic notation, making it almost a virtue to proceed "without the help of letters" (absque litterarum auxilio). Presumably he knew of the prescient French algebraist Viète, who wrote some two generations earlier. This vignette catches algebra at a stage where it was just about to start its great ascent, where verbal explanations were perfectly acceptable, sometimes even preferred. It does reinforce one's appreciation for "the help of letters". Here is an extract from Potestatum Numericarum Summa:

   First, the sum of the proposed numbers, 5 + 8 + 11 + 14, namely 38, is multiplied by 108, leading to the product 4104.
   Then the sum of the squares of the proposed numbers, that is, 5² + 8² + 11² + 14², namely 25 + 64 + 121 + 196, whose sum is 406, is multiplied by 54 to make 21924.
   Next the number 5 is taken to the fourth power, which is 625.
   Finally the number 3 is taken to the fourth power, giving 81, which becomes 324 when multiplied by four. So the numbers subtracted are 4104, 21924, 625, and 324, whose sum is 26977, which leaves 56544 when subtracted from the number 83521.
   This remainder therefore is the sum asked for, 4712, multiplied by 12; and in fact, 4712 multiplied by 12 makes 56544.

The screenshots are from the 1923 issue of Œuvres de Blaise Pascal in the Les Grands Écrivains de la France series (The Great Writers of France). A French version appears there opposite the original Latin, shown above; the French title is Sommation des puissances numériques. The entire article is less than eight pages in the original Latin.

Put \( \displaystyle{s_p(n) = {\sum_{k=1}^n k^p} ={1^p + 2^p + 3^p + \cdots + n^p}.} \) Using Pascal's method, \( s_p(n) \) can be shown to be a polynomial in \( n \) of degree \( p + 1 \). Consider \( s_2(n) = {\sum_{k=1}^n k^2}, \) for example. Proceeding as in Pascal's example, but with the upper limit being the indeterminate \( n: \)
\begin{align*}
(n+1)^3 - n^3 &= 3n^2 + 3n + 1\\
n^3 - (n-1)^3 &= 3(n-1)^2 + 3(n-1) + 1\\
(n-1)^3 - (n-2)^3 &= 3(n-2)^2 + 3(n-2) + 1\\
\vdots\\
2^3 - 1^3 &= 3 \cdot 1^2 + 3 \cdot 1 + 1\\
1^3 - 0^3 &= 0^2 + 3 \cdot 0 + 1
\end{align*}
Adding them all up leads to the following, considering that almost everything on the left collapses:
\begin{equation}{(n+1)^3 = 3 \cdot \color{red}{\sum_{k=0}^n k^2} + 3 \cdot \sum_{k=0}^n k + n + 1.}\tag{2} \end{equation}
All that remains is to solve for \( \color{red}{\sum_{k=0}^n k^2}, \) assuming that \( \sum_{k=0}^n k \) is known (and it is: \( \sum_{k=0}^n k = n (n+1)/2): \)
\begin{align}
\color{red}{\sum_{k=0}^n k^2} &= {1 \over 3} \left((n+1)^3 - n - 1 - 3 \cdot \sum_{k=0}^n k \right)\\
&= {1 \over 3} \left(n^3 + 3 n^2 + 2n - 3 \cdot {n(n+1) \over 2} \right)\\
&= {1 \over 6} \left(2\left(n^3 + 3 n^2 + 2n\right) - 3n(n+1) \right)\\
&= {1 \over 6} \left( 2n^3 + 3n^2 + n \right)\\
&= {{1 \over 3}n^3 + {1 \over 2}n^2 + {1 \over 6}n},
\end{align}
which agrees with equation (1) at the top. Equation (2) can be written:
\[ (n+1)^3 = 3 \cdot s_2(n) + 3 \cdot s_1(n) + s_0(n) + 1.\]
Pascal's method shows, in general, that for integers \( p \geq 0, \; n \geq 0: \)
\begin{equation}{(n+1)^{p+1} - 1 = \sum_{k=0}^p \binom{p+1}{k} s_k(n).}\tag{3} \end{equation}
The proof is just like that for \( p = 2 \) discussed above. And like in that example, you can solve for \( s_p(n) \) in terms of the earlier \( s_k(n), \) where \( k \lt p, \) and of \( (n+1)^{p+1} - 1.\) Considering \( s_p(n) \) as unknown in equation (3), the greatest power of \( n \) encountered on the right hand side is \( n^p \) and the left hand side is a polynomial of degree \( n^{p+1}, \) the coefficient of \( n^{p+1} \) being one. All coefficients are rational. So solving for \( s_p(n) \) results in a polynomial in \( n \) of degree \( p + 1 \) with rational coefficients. The multiplier of \( s_p(n) \) in (3) is \( \binom{p+1}{p} = p+1, \) so the \( n^{p+1} \) term (one) will be divided by \( p+1 \) when solving for \( s_p(n). \) Furthermore, \( s_p(n) \) has no constant term and all its coefficients sum to one (evaluate at \( n = 0 \) and \( n = 1 \) respectively). To sum up:

\( s_p(n) = {\sum_{k=1}^n k^p} ={1^p + 2^p + 3^p + \cdots + n^p} \) is a polynomial in \( n \) of degree \( p + 1 \) with rational coefficients. The coefficient of \( n^{p+1} \) is \( 1 / (p+1). \) There is no constant term and all the coefficients sum to \( 1. \)

Around 1650 there was great interest in quadrature, that is, calculating areas under curves, or integration in our parlance. Remember the timing; Descartes' La Géométrie had been published in 1637, but it was obscure and opaque. Van Schooten published epochal editions in 1649 and (especially) 1659-61 that contained a great deal more commentary than there was text from Descartes. These were the texts transmitting the new analytic geometry and Pascal was right there with this contribution. Here he is explaining the connection with integration:

Conclusion.

   Anyone at all familiar with the doctrine of indivisibles will see what one can draw from all this for the determination of curvilinear areas. For all at once it is now easy to measure all kinds of parabolas and many other curves as well.
   If we apply this numerical method to continuous quantities, we can state these rules:

Rules for summing progressions of natural numbers starting with one:

The sum of linear terms is to the square of the largest as 1 is to 2.
The sum of squares is to the cube of the largest as 1 is to 3.
The sum of cubes is to the fourth power of the largest as 1 is to 4.

He goes on to state the \( 1 / (p+1) \) rule for "all kinds of parabolas", that is, for \( y = x^p, \) where \( p \) is any natural number. The idea is that the area under a parabola can be decomposed into a series of small rectangles becoming virtually lines as their widths decrease indefinitely, and insofar as the equation of a simple parabola is \( y = x^2, \) the height of a line at \( x = k/n \) is \( y = (k/n)^2. \) So the height of all those little rectangles taken together includes:
\[ s_2(n) = 1^2 + 2^2 + \cdots + n^2 = {n^3 \over 3} + \text{expression involving lower powers of } n. \]
All that is divided by \( n^2 \) and by another \( n \) to account for the width of each rectangle. The "expression involving lower powers of \( n \)" washes out as \( n \) increases indefinitely and all that remains in the end is the \( 1/3 \) and that is the area under the parabola. In Pascal's words:

Sic puncta lineis, lineae superficiebus, superficies solidis nihil adjiciunt ... Quare, inferiores gradus, nullius valons existentes, non considerandi sunt.
So points add nothing to lines, lines to surfaces, or surfaces to solids ... This is why lower powers are to be disregarded as having no value.

Riemann Sum for a parabola

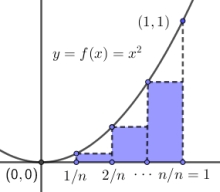
This is all perfectly solid, and to put it in modern notation, calculate a lower Riemann sum for \( y = f(x) = x^2 \) between \( 0 \) and \( 1 \) as pictured. Take \( n + 1 \) equally spaced points for the partition: \( \{0 = 0/n, 1/n, 2/n \cdots (n-1)/n, n/n = 1\}. \) Add up the areas of all the thin rectangles under the curve determined by those partition points and take the limit as \( n \rightarrow \infty : \)
\begin{align}
S_n(x^2) &= {{1 \over n} \cdot f\left({1 \over n}\right) + {1 \over n} \cdot f\left({2 \over n}\right) + \cdots + {1 \over n} \cdot f\left({{n-1} \over n}\right)}\\
&= {1 \over n} \cdot \left(\left({1 \over n}\right)^2 + \left({2 \over n}\right)^2 + \cdots + \left({{n-1} \over n}\right)^2 \right)\\
&= {1 \over n^3} \left(1^2 + 2^2 + \cdots + (n-1)^2 \right)\\
&= {1 \over n^3} \left({1 \over 3} (n-1)^3 + \text{ polynomial in } n \text { of degree } 2 \right)\\
&= {1 \over n^3} \left({1 \over 3} n^3 + \text{ polynomial in } n \text { of degree } 2 \right)\\
&= {1 \over 3} + {{\text{ polynomial in } n \text { of degree } 2} \over n^3} \longrightarrow {1 \over 3}.
\end{align}
\[ \therefore \; \int_{0}^{1} x^2 dx = \lim_{n \to \infty} S_n(x^2) = {1 \over 3}. \]

Pascal's \( 1 / (p+1) \) rule for the sum of the \( p^{\text{th}} \) powers shows similarly that:
\[ \int_{0}^{1} x^p dx = \lim_{n \to \infty} S_n(x^p) = {1 \over {p+1}}. \]
Thinking of an integral as area under the curve, it's clear that:
\[ \int_{0}^{1} \left(ax^p + bx^q\right) dx = a \int_{0}^{1} x^p dx + b \int_{0}^{1} x^q dx, \hspace{20px} a \geq 0, \; b \geq 0, \; p, q \in \mathbb{N}. \]
The \( x-\)axis could have been partitioned between \( x = 0 \) and \( x = c, \) for any \( c \geq 0, \) each increment along the axis measuring \( c/n \) instead of \( 1/n, \) leading to the formula:
\[ \int_{0}^{c} x^p dx = {c^{p+1} \over {p+1}}, \hspace{20px} c \geq 0, \; p \in \mathbb{N}. \]
The crux of it all is that Pascal was able to integrate any polynomial. This is a little anachronistic, considering that van Schooten and his associates were laying down the foundations of analytic geometry just at this moment. But not much, considering how they and other workers were able to proceed as I've indicated, given this work of Pascal's.

The universities throttled European mathematics until its reawakening in the late fifteenth century under the aegis of Regiomontanus (1436-1476), Tartaglia (1499-1557), Cardano (1501-1576), and a few others. The advent of printing quickened the phenomenon, as Elizabeth Eisenstein has so cogently explained^[4] — the case for Regiomontanus is particularly good, considering his extensive printing program. I say "reawakening", because the abortive translation movement of the twelfth and thirteenth centuries (from Arabic and Greek to Latin) revived Aristotle, but even that served to plow mathematics under. Paul Lawrence Rose explained how Fibonacci's promise of an auspicious beginning in the early 13th century was ignored for three hundred years except by the merchants' abacus schools and the surveyors. Bowdlerized Euclids held reign in the schools, often without proofs.^[5] Scholastics had access to Moerbeke's thirteenth century translation of Archimedes, but perverted him as if with an intent to kill. Only by overcoming this deeply reactionary intellectual tradition could the new mathematics truly revive the Archimedean tradition and start the long march to modern mathematics. Tartaglia, for example, was an accountant; Regiomontanus had close contact with the universities but was not a professor. Nor did Pascal have a university post a century later and just as well — he would have been smothered there.

Much like Descartes and the other intellectual innovators of the period, Pascal wrote mathematics in a narrative fashion with examples, so unlike the formal Euclidean approach favored in the universities, terminally in thrall to formal logic, tradition, and Aristotle. It is possible to recognize Euclid's Elements as one of the finest works of mathematics of all time and one of the greatest textbooks down the ages and at the same time acknowledge how slavish devotion to it can, and at that time did, have a stultifying effect. Like his contemporaries Descartes and Wallis in England (who derived the \( 1 / (p+1) \) rule by examining examples), Pascal connected geometry and numbers — that is, he helped found analytic geometry. He might be criticized for the hand-waving notion of indivisibles, blurring the distinction between lines and small rectangles. He shared this with Newton, Leibnitz, and the other founders of calculus, who somehow managed to create timeless mathematics without a solid logical foundation until Cauchy and the rest laid that foundation in the nineteenth century. It was absolutely necessary to break the chains of tradition in order to progress and that is exactly what Pascal and like-minded contemporaries did as they created a lasting legacy.

Mike Bertrand

June 25, 2018

^ 1. Traité du triangle arithmétique (Treatise on the Arithmetic Triangle), by Blaise Pascal (written 1654, published 1665).

^ 2. Pascal's Arithmetical Triangle, by A. W. F. Edwards, The Johns Hopkins University Press (2002, originally published 1987), ISBN 0-8018-6946-3.

^ 3. Potestatum Numericarum Summa (The Sum of Powers of Numbers), by Blaise Pascal (written 1654, published 1665).

^ 4. The Printing Press as an Agent of Change, by Elizabeth Eisenstein, Cambridge University Press (1980), ISBN 0521-22044-0.

^ 5. The Italian Renaissance of Mathematics, by Paul Lawrence Rose, Librairie Droz (1975), ISBN 978-2-600-03059-5. Fibonacci's promise: p 83; perverted him: p 80. The central thesis of this remarkable book is that Italian humanist mathematics revived the Archimedean tradition outside the universities, and it was this tradition that led to modern mathematics. I might add that the universities did adapt in the seventeenth century, but slowly, the Jesuits leading the way (Descartes was Jesuit-trained, for example).

Other references:

• "Pascal's Formula for the Sums of Powers of the Integers", by Carl B. Boyer, Scripta Mathematica 9 (1943), pp 237-244. Good historical background on antecedents to Pascal work on sums of powers. Contains an English translation of some of the Potestatum.

• Mathematical Masterpieces, by Arthur Knoebel, et al., Springer (2007), ISBN 978-0-387-33060-0. An English translation of the Potestatum appears on pp 32-37 (from the French in the 1923 Grands Écrivains edition). Good discussion is had just before and after the Potestatum itself.