Euler Proves Fermat's Theorem on the Sum of Two Squares

The theorem in question is:

If \( p \) is an odd prime with \( p \equiv 1 \; (\text{mod} \; 4), \) then \( p \) is the sum of two squares.\( (1) \)

Only if is easy, because for all natural numbers \( n, \; n^2 \equiv 0, 1 \; (\text{mod } 4), \) so \( n^2 + m^2 \equiv 0, 1, 2 \; (\text{mod} \; 4) \) and a sum of two squares cannot be congruent to \( 3 \; (\text{mod} \; 4). \) Obviously \( 2 = 1^2 + 1^2 \) as well. The Brahmagupta-Fibonacci identity assures that a product of sums of two squares is itself a sum of two squares:

\[ \begin{equation}{(a^{2}+b^{2})(c^{2}+d^{2})=(ac+bd)^{2}+(ad-bc)^{2}.}\tag{2} \end{equation} \]

So a natural number whose prime power decomposition contains only \( 2 \)s and primes congruent to \( 1 \; (\text{mod} \;4) \) is itself a sum of squares. With \( (a, b, c, d) = (2, 1, 3, 2), \) for example,

\[ 5^2 \cdot 13^2 = (2^2 + 1^2)(3^2 + 2^2) = 65 = (2\cdot 3 + 1 \cdot 2)^2 + (2\cdot 2 - 1 \cdot 3)^2 = 8^2 + 1^2. \]

The problem goes back (at least) to Diophantus, who in the Greek geometric tradition sought right triangles on a given hypotenuse with integer sides. According to Leonard Dickson in History of the Theory of Numbers^[1] (p. 227):

A. Girard (Dec 9, 1632) had already made a determination of the numbers expressible as a sum of two integral squares: every square, every prime \( 4n + 1, \) a product formed of such numbers, and the double of one of the foregoing.

Girard knew of Diophantus and this is correct and provable with Euler's help. Fermat of course was an acolyte and editor of Diophantus and posited many results connected to this problem, including on the number of ways such sums can be formed. Quoting Dickson again (p. 228):

Fermat called the theorem that every prime \( 4n + 1 \) is the sum of two squares [cited henceforth as Gerard's theorem] the fundamental theorem on right triangles. He stated that he possessed an irrefutable proof. Elsewhere he stated that his proof was by the method of infinite descent: "If a prime \( 4n + 1 \) is not a sum of two squares, there exists a smaller prime of the same nature, then a third still smaller, etc., until the number \( 5 \) is reached," thus leading to a contradiction.

The first claim of a proof is in a letter to Pascal in 1654, but no such proof is extant. Fermat is known to have made highly unlikely assertions of this kind (notoriously, for his "Last Theorem"), but Euler had the very highest opinion of him and credited the claim, calling it "Fermat's Theorem", as I do in the title of this article. Girard's formulation can be put on a firm foundation as follows (see Dummit & Foote, 3rd ed., p. 291):

Let \( n = 2^k p_1^{a_1} \cdots p_r ^{a_r} q_1^{b_1} \cdots q_s ^{b_s} \), where the \( p_i \) are distinct primes with \( p_i \equiv 1 \; (\text{mod} \; 4) \) and the \( q_i \) are distinct primes with \( q_j \equiv 3 \; (\text{mod} \; 4). \) Then \( n \) is the sum of two squares if and only if all the \( b_j \) are even.

The "if" part follows directly from the Brahmagupta-Fibonacci identity if we can assume that primes congruent to \( 1 \; (\text{mod} \; 4) \) are sums of two squares, keeping in mind that \( 2 \) is a sum of two squares and the remaining factor is itself a square. The "only if" part follows from Euler's propositions below, as spelled out here.

Euler first attempted a proof in De Numeris Qui Sunt Aggregata Duorum Quadratorum (On Numbers Which Are the Sum of Two Squares)^[2], published in 1758, E228 in the canonical Eneström Index. Paul Bialek has an English translation. There are four key propositions:

If the product \( pq \) is a sum of two squares and one factor \( p \) is a prime number and itself a sum of two squares, then the other factor \( q \) will also be a sum of two squares.

Proof: Proceeding as Euler did, let \( pq = a^2+b^2 \) where \( p = c^2 + d^2 \) is prime. \( c \) and \( d \) are relatively prime, because any common factor would divide the prime number \( p. \) Charmingly, Euler uses \( aa \) instead of \( a^2 \) for a square, as older writers had. By hypothesis:

\[ pq = (c^2 + d^2) q = a^2 + b^2. \]

Therefore \( c^2 + d^2 \; | \; a^2 + b^2 \; | \; c^2(a^2 + b^2) \) and obviously \( c^2 + d^2 \; | \; a^2(c^2 + d^2), \) so \( c^2 + d^2 \) divides the difference of the two right-hand sides. That is:

\[ c^2 + d^2 \; | \; c^2(a^2 + b^2) - a^2(c^2 + d^2) = b^2 c^2 - a^2 d^2 = (bc - ad)(bc + ad). \]

\( p = c^2 + d^2 \) being prime, this forces \( c^2 + d^2 \; | \; bc - ad \) or \( c^2 + d^2 \; | \; bc + ad. \) Suppose \( c^2 + d^2 \; | \; bc - ad, \) with \( bc - ad = m(c^2 + d^2). \) Let \( x \) and \( y \) be such that:

\[ \begin{align*}
b &= mc + x, \\
a &= -md + y.
\end{align*} \]

\[ \begin{align*}
\therefore bc - ad &= (mc + x)c - (-md + y)d \\
&= mc^2 + xc + md^2 - yd \\
&= m(c^2 + d^2) + (xc - yd) \\
&= (bc - ad) + (xc - yd).
\end{align*} \]

Therefore \( (xc - yd) = 0, \) or \( xc = yd. \) Since \( c \) and \( d \) are relatively prime, this implies \( d\; | \; x, \) so \( x = nd \) for some \( n, \) \( yd = xc = (nd)c, \) and \( y = nc. \)

\[ \begin{align*}
\therefore b = mc + x &= mc + nd, \\
a = -md + y &= -md + nc.
\end{align*} \]

Substituting for \( a \) and \( b: \)

\[ \begin{align*}
pq &= a^2 + b^2 \\
&= (-md + nc)^2 + (mc + nd)^2 \\
&= (m^2 d^2 -2mncd + n^2 c^2) + (m^2 c^2 +2mncd + n^2 d^2) \\
&= m^2 d^2 + n^2 c^2 + m^2 c^2 + n^2 d^2) \\
&= (m^2 + n^2)(c^2 + d^2),
\end{align*} \]

from which it follows that the quotient \( q = m^2 + n^2. \) Assuming \( c^2 + d^2 \; | \; bc + ad \) above rather than \( c^2 + d^2 \; | \; bc - ad \) would have proceeded in the same way. QED.

If the product \( pq \) is a sum of two squares but its factor \( q \) is not a sum of two squares, then the other factor \( p \) has at least one prime factor which is not a sum of two squares.

Proof. If \( p \) is prime and a sum of two squares, then by Proposition 1, \( q \) is the sum of two squares, but it's not, so \( p \) is not the sum of two squares. Assume \( p = p'p'', \) where \( p' \) and \( p'' \) are both primes equal to the sum of two squares. Then since \( pq = (p'p'')q = p'(p''q) \) and prime \( p' \) are sums of two squares, then so is \( p''q \) by Proposition 1. Applying Proposition 1 again, \( q \) would have to be the sum of two squares, but it's not. The contradiction implies that at least one of \( p' \) or \( p'' \) is not a sum of two squares. The proof procceeds similarly in general — \( p \) cannot equal a product of primes all of which are a sum of two squares. They can be peeled off one by one to force a contradiction. It follows that at least one of the prime factors of \( p \) is not the sum of two squares. QED.

Here is Proposition 3 and its proof straight from Euler:

PROPOSITIO 3

Si summa duorum quadratorum inter se primorum \( aa + bb\) divisibilis sit per numerum \(p, \) semper exhiberi poterit summa duorum aliorum quadratorum \( cc + dd \) divisibilis per eundem numerum \( p, \) ita ut ista summa \( cc + dd \) non sit maior quam \( {1 \over 2} pp. \)

DEMONSTRATIO

Sit summa duorum quadratorum inter se primorum \( aa + bb \) divisibilis per numerum \( p \) et \( a \) et \( b \) numeri quantumvis magni. Quia ergo neque \( a \) neque \( b \) seorsim per \( p \) divisibilis est, numeri \( a \) et \( b \) ita exprimi poterunt, ut sit \( a = mp \pm c \) et \( b = np \pm d, \) ubi numeros \( m \) et \( n \) ita determinare licet, ut \( c \) et \( d \) non excedant semissem ipsius \( p. \) Erit ergo \[ aa + bb = mm pp \pm 2mcp + cc + nn pp \pm 2ndp + dd, \] quae formula cum et tota divisibilis sit per \( p \) (per hypothesin) et eius pars \( mmpp \pm 2mcp + nnpp \pm 2ndp \) per se divisorem habeat \( p, \) necesse est, ut altera pars \( cc + dd, \) quae est summa duorum quadratorum, itidem per \( p \) sit divisibilis. At cum radices \( c \) et \( d \) non excedant semissem ipsius \( p, \) summa quadratorum \( cc + dd \) non excedet quadratum \( {1 \over 4} pp \) bis sumtum; ideoque summa duorum quadratorum \( cc + dd \) exhiberi potest non maior quam \( {1 \over 2} pp, \) quae tamen sit per p divisibilis. Q. E. D.

He uses \( aa \) for \( a^2 \) and the letter \( p \) does not necessarily represent a prime; other than that, it could have been written yesterday, were Latin still in vogue. Here it is in English:

PROPOSITION 3

If a sum of two relatively prime squares \( a^2 + b^2 \) is divisible by a number \( p, \) it is always possible to produce two other squares \( c^2 + d^2 \) divisible by \( p, \) such that the sum \( c^2 + d^2 \) does not exceed \( {1 \over 2} p^2. \)

DEMONSTRATION

Let a sum of two relatively prime squares \( a^2 + b^2 \) be divisible by the number \( p, \) however large \( a \)and \( b. \) Since \( a \) and \( b \) cannot both be divisible by \( p, \) the numbers \( a \) and \( b \) can be expressed as \( a = mp \pm c \) and \( b = np \pm d, \) where the numbers \( m \) and \( n \) are chosen such that \( c \) and \( d \) do not exceed half of \(p. \) Therefore:\[ \begin{equation}{a^2 + b^2 = m^2 p^2 \pm 2mcp + c^2 + n^2 p^2 \pm 2ndp + d^2,}\tag{3} \end{equation} \] where since the whole is divisible by \( p \) (by hypothesis) and the part \( m^2 p^2 \pm 2mcp + n^2 p^2 \pm 2ndp \) is divisible by \( p, \) the other part \( c^2 + d^2 \) must also be divisible by \( p. \) And since \( c \) and \( d \) do not exceed half of \(p, \) the sum of squares \( c^2 + d^2 \) will not exceed \( {1 \over 4} p^2; \) therefore a sum of two squares \( c^2 + d^2 \) can be produced not greater than \( {1 \over 2} p^2 \) and also divisible by \( p. \) QED.

Proof. To put it in my words: \( p \) does not divide both \( a \) and \( b, \) since otherwise \( a \) and \( b \) would not be relatively prime. So there are \( c \) and \( d, \) not both zero, such that:

\[ \textstyle a = mp + c, \;\; |c| \leq {1 \over 2} p \\ \textstyle b = np + d, \;\;\; |d| \leq {1 \over 2} p. \]

\[ \begin{align*}
\therefore c^2 + d^2 &= (a - mp)^2 + (b - np)^2 \\
&= a^2 + b^2 + p(-2m + mp - 2n + np)
\end{align*} \]

Since \( p \) divides \( a^2 + b^2, \) \( p \) also divides \( c^2 + d^2 \). Also:

\[ c^2 + d^2 \leq {1 \over 4} p^2 + {1 \over 4} p^2 = {1 \over 2} p^2. \]

QED.

Note that \( p \) can be any whole number in Proposition 3 and is not necessarily a prime. Also that \( c \) and \( d \) are not necessarily relatively prime. This is a shortcoming, because the proof of Proposition 4 coming next requires \( c \) and \( d \) to be relatively prime in order to develop an iterative process. Harold Edwards fills the gap^[3] (p. 46-48) and the Wikipedia page on proofs of this theorem recapitulates Edwards. We do know that \( p \; | \; c^2 + d^2, \) so \( c^2 + d^2 = yp \) for some \( y. \) Let \( g = \text{gcd}(c, d). \) Then \( \text{gcd}(g, p) = 1, \) otherwise \( a \) and \( b \) have a common factor by virtue of (3). So \( g^2 \; | \; y \) and the fractions in this equation are all integers:

\[ {\left({c \over g}\right)^2 + \left({d \over g}\right)^2} = {{y \over g^2} \cdot p}. \]

Therefore \( c' = {c / g} \) and \( d' = {d / g} \) satisfy the conditions of Proposition 3 with \( c' \) and \( d' \) relatively prime, namely, \( p \; | \; c'^2 + d'^2 \) and \( c'^2 + d'^2 \leq c^2 + d^2 \leq {1 \over 2} p^2. \) QED'.

If \( a \) and \( b \) are relatively prime, then every factor of \( a^2 + b^2 \) is itself the sum of two squares.

Proof. Suppose \( p \; | \; a^2 + b^2, \) where \( a \) and \( b \) are relatively prime. By Proposition 3, there are relatively prime \( c \) and \( d \) such that \( p \; | \; c^2 + d^2, \) where \( c^2 + d^2 \leq {1 \over 2} p^2. \) Say \( c^2 + d^2 = pq. \) If \( p \) is not the sum of two squares, then by Proposition 2, \( q \) has a factor \( r \) that is not the sum of two squares. We have

\[ \textstyle pq = c^2 + d^2 \leq {1 \over 2} p^2. \]

\[ \textstyle \therefore r \leq q \leq {1 \over 2} p. \]

Again by Proposition 3, applied to \( r \) and \( c^2 + d^2, \) there are relatively prime \( e \) and \( f \) such that \( r \; | \; e^2 + f^2, \) where \( e^2 + f^2 \leq {1 \over 2} r^2 \leq {1 \over 2}({1 \over 2} p)^2 = {1 \over 8} p^2. \) We could continue in this fashion producing smaller and smaller numbers, each of which is a sum of two squares divisible by a number which is not a sum of two squares. But there are no such cases among the smallest numbers, so the original assumption that \( p \) is not the sum of two square is untenable. QED.

Click image for a geometric proof of the irrationality of \( \sqrt{2} \) (same as the incommensurability of the side and diagonal of a square).

This is an example of the celebrated proof by infinite descent practiced by Fermat and known to the ancient Greeks, who most likely proved that \( \sqrt{2} \) is irrational by an infinite sequence of smaller and smaller squares (\( \varphi = {{(\sqrt{5} + 1)} / 2} \) too using pentagons). It's superfluous even to note that there are no instances among the smallest integers at the end:

Et cum \( r \) non sit summa duorum quadratorum, simili modo procedendo continuo ad minores summas duorum quadratorum deveniretur, quae per numerum non-summam duorum quadratorum essent divisibiles. Quocirca, cum in minimis numeris nulla detur summa duorum quadratorum inter se primorum, quae esset divisibilis per numerum, qui non sit summa duorum quadratorum, ne in maximis quidem numeris eiusmodi erunt summae duorum quadratorum, quae divisibiles sint per numeros, qui ipsi non essent summae duorum quadratorum.

And since \( r \) is not a sum of two squares, proceeding continuously in a similar way reaches smaller sums of two squares which are divisible by the number which is not the sum of two squares. Therefore, since among the smallest numbers none is given which is the sum of relatively prime squares, which is divisible by a number which is not the sum of two squares, neither among the largest numbers will there be a sum of two squares, which is divisible by numbers which themselves are not sums of two squares.

Euler has proven that the initial assumption implies the existence of an infinite strictly-decreasing sequence of whole numbers, an impossibility invalidating the assumption.

Euler finished the proof in Demonstratio theorematis Fermatiani omnem numerum primum formae \( 4n + 1 \) esse summam duorum quadratorum (Demonstration of a Theorem of Fermat That Every Prime Number of the Form 4n + 1 is the Sum of Two Squares)^[4], published in 1760 (E241). Mark R. Snavely and Phil Woodruf have an English translation. Euler says towards the start, speaking of the paper just discussed:

Tentamen tamen demonstrationis tum exposui, unde certitudo huius theorematis multo luculentius elucet, etiamsi criteriis rigidae demonstrationis destituatur, neque dubitavi, quin iisdem vestigiis insistendo tandem demonstratio desiderata facilius obtineri possit; quod quidem ex eo tempore mihi ipsi usu venit, ita ut tentamen illud, si alia quaedam levis consideratio accedat, in rigidam demonstrationem abeat.

Next I attempted to give a demonstration showing clearly the certainty of this theorem, even while falling short of having an absolutely rigorous proof. I did not doubt that by continuing with such methods, the desired proof would finally be easily obtained, since from that time it came to me by experimenting that this attempt, if certain other considerations should agree, would become a rigorous proof.

He says he needs Proposition 4, and also that:

If \( p \) is prime with \( p \not| \; a, \; p \not| \; b, \) then \( p \; | \; a^{p-1} - b^{p-1}. \)\( (4) \)

This is a consequence of Fermat's Little Theorem, that with these hypotheses \( a^{p-1} \equiv b^{p-1} \equiv 1 \; (\text{mod} \; p). \)

The crux of the argument is quickly reached in §3 and §4. Let \( p = 4n + 1 \) be prime, \( p \not| \; a, \; p \not| \; b, \) where \( a \) and \( b \) are relatively prime. Then by (4), \( p \; | \; a^{4n} - b^{4n} = (a^{2n} + b^{2n})(a^{2n} - b^{2n}), \) so prime \( p \) divides one of these factors. If there are any \( a \) and \( b \) such that \( p \; | \; a^{2n} + b^{2n}, \) then we are done, applying Proposition 4. So it suffices to show that it is not always the case that \( p \; | \; a^{2n} - b^{2n}. \) In Euler's words:

Quodsi iam demonstrari posset dari casus, quibus forma \( a^{2n} + b^{2n} \) sit divisibilis per \( 4n + 1, \) quoniam \( a^{2n} + b^{2n} \) ob exponentem \( 2n \) parem est summa duorum quadratorum, quorum neutrum seorsim per \( 4n + 1 \) divisibile existit, inde sequeretur hunc numerum \( 4n + 1 \) esse summam duorum quadratorum. ... Quamobrem mihi hic demonstrandum est non omnes numeros in forma \( a^{2n} - b^{2n} \) contentos per \( 4n + 1 \) esse divisibiles; hoc enim si praestitero, certum erit dari casus seu numeros pro \( a \) et \( b \) substituendos, quibus forma \( a^{2n} - b^{2n} \) non sit per \( 4n + 1 \) divisibilis; illis ergo casibus altera forma \( a^{2n} + b^{2n} \) necessario per \( 4n + 1 \) erit divisibilis. Unde, cum \( a^{2n} \) et \( b^{2n} \) sint numeri quadrati, conficietur id, quod proponitur,, scilicet numerum \( 4n + 1 \) esse summam duorum quadratorum.

If it can be shown that \( a^{2n} + b^{2n} \) is divisible by \( 4n + 1,\) then it would follow that the number \( 4n + 1 \) is the sum of two squares, due to the even exponents and the fact that \( 4n + 1 \) divides neither \( a \) nor \( b. \) ... So I have to prove that not all numbers of the form \( a^{2n} - b^{2n} \) are divisible by \( 4n + 1. \) For if I show that there are \( a \) and \( b \) such that \( a^{2n} - b^{2n} \) is not divisible by \( 4n + 1, \) then the other factor \( a^{2n} + b^{2n} \) is necessarily divisible by \( 4n + 1. \) Since \( a^{2n} \) and \( b^{2n} \) are square, the proposed theorem is proven, namely, that the number \( 4n + 1 \) is a sum of two squares.

Euler looks at the \( 2n + 1 \) numbers:

\[ 1^{2n}, \; 2^{2n}, \; 3^{2n}, \; 4^{2n}, \cdots \; (2n)^{2n}, (2n + 1)^{2n}. \]

Take their differences:

\[ \begin{equation}{2^{2n} - 1^{2n}, \; 3^{2n} - 2^{2n}, \; 4^{2n} - 3^{2n}, \cdots (2n + 1)^{2n} - (2n)^{2n}.} \tag{5} \end{equation} \]

Progressive differences of the first few cubes.

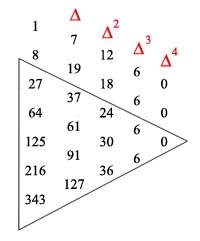
Two adjacent values from the first list are candidates for \( a \) and \( b \), considering that they are relatively prime — Euler wants to prove that \( p \) does not divide all the differences \( \Delta \) in (5). Suppose it did. Then \( p \) would divide the differences of the differences \( \Delta^2. \) And the differences of those differences \( \Delta^3, \) and so on. But a key fact from the calculus of finite differences says that \( \Delta^m x^m = m!. \) This is true for any contiguous sequences of \( m \) integers and Euler takes a fair amount of time motivating and proving this result. So if \( p \) were to divide all the differences in (5), then \( p | (2n)!, \) but this is out of the question, since \( p \) is a prime greater than \( 2n. \) The main theorem follows: \( p = 4n + 1 \) must be the sum of two squares. QED.

Mike Bertrand

September 7, 2016

^ 1. History of the Theory of Numbers, Vol. II, by Leonard Dickson (Carnegie Institute of Washington, 1920). Chapter VI takes up the sum of two squares problem in detail.

^ 2. De numeris qui sunt aggregata duorum quadratorum (On Numbers which are the Sum of Two Squares), by Leonhard Euler, Opera Omnia, 2, p 295-327. Originally published in 1758.

^ 3. Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory, by Harold M. Edwards, (Springer-Verlag, 1977).

^ 4. Demonstratio theorematis Fermatiani omnem numerum primum formae \( 4n + 1 \) esse summam duorum quadratorum (Demonstration of a Theorem of Fermat That Every Prime Number of the Form \( 4n + 1 \) is the Sum of Two Squares), by Leonhard Euler, Opera Omnia, 2, p 328-337. Originally published in 1760.