Emmy Noether's Idealtheorie — How She Proved Primary Decomposition

Emmy Noether Google Doodle for March 23, 2015

There are people great and small who sense the future with a clairvoyance not given to the rest of us, seers with a preternatural instinct for the arc of what is to come. Abraham Lincoln was one, Emmy Noether another in the world of mathematics. She was the daughter of a German mathematics professor renowned in his day,^[1] a lucky fluke in a society with little use for women as thinkers and academics. Emmy Noether revolutionized mathematics in the early twentieth century by identifying and explaining the underlying abstract principles behind the mathematics bequeathed to her. Like all geniuses, indeed all human beings, she existed in a social context. Asked to explain her deep insights, she would say "Es steht alles schon bei Dedekind" (Everything is already there in Dedekind)^[2], and that is not false modesty. Not false modesty, but modesty all the same, because she was second to none in triggering a new direction in mathematics.

The term "abstraction" has the connotation of distilling the essence of something (from the Latin abstrahere, to draw off from). Let her student and disseminator B. L van der Waerden define it:

The quantities employed in algebraic and arithmetic operations vary in nature; at times we use the integers, or the rational, the real, complex or algebraic numbers, and at other times we deal with polynomials, or rational functions in n variables, etc. Later on we shall become familiar with quantities of a completely different nature, such as hypercomplex numbers, residue classes, etc., with which we can operate in the same or almost the same manner as with numbers. It is, therefore, desirable to arrive at a common concept embracing all these domains, and to investigate the rules of operation in these domains in general.^[3]

Axioms for a ring in Idealtheorie in Ringbereichen

One of her great papers was Idealtheorie in Ringbereichen (Ideal Theory in Ring Domains)^[4] in 1921, where she stated and proved the primary decomposition theorem for Noetherian rings, as they are called today. She wasn't the first to define a ring in the modern sense, but close. She gives the modern definition of a commutative ring in Idealtheorie as shown in this screen shot, modifying Abraham Fraenkel's more restrictive axioms of 1914 in his doctoral dissertation — footnote 7 at "abstrakter Definition" on the second line of the screenshot cites Fraenkel. Here is the testimony of Robert of Robert Gilmer:

The year 1920 also marks a turning point in Emmy Noether's career. It was then that she began to be recognized as a mathematician in her own right, as opposed to an assistant of Hilbert and Klein. By 1923, she was recognized as the leader of the Göttingen School of Algebra, a position she maintained until her departure from Göttingen in 1933. He monumental paper Idealtheorie in Ringbereichen, published in 1921, was responsible for much of the recognition she received; its elegant, axiomatic approach was novel in the area at the time, but more than anything else, she gained the attention and respect of the mathematical community because of the results she obtained. For Noether did more than generalize results known for polynomial rings to rings satisfying the ascending chain condition for ideals; in addition to that, she proved significant new results that had not been proved for polynomial rings. Her results tangibly indicated the power of the axiomatic approach and the wealth of good mathematics it was to yield.^[5]

She writes that the existence of the zero element follows from the ring axioms, that a ring need not have a unit, and that the product of two elements can be zero without either of the factors being zero. She says that rings without such zero divisors and with a unit are called integral domains (eigentliche Integritātsbereiche).^[6] It seems routine today, but only because the concepts she laid out here one hundred years ago became canonical from virtually the moment she set them down. A moment's pause is in order to reflect on the fact that something is being born here, this is the start.

She notes that when \( n \) is a natural number and \( a \) an element of the ring, then the notation \( na \) denotes \( a + a + \cdots + a,\) where there are \( n \) copies of \( a, \) and continues:

Let an ideal \( \mathfrak{M} \) in \( \Sigma \) be understood to be a system of elements of \( \Sigma \) such that the following two conditions are satisfied:
1. If \( \mathfrak{M} \) contains \( f, \) then \( \mathfrak{M} \) also contains \( a \cdot f, \) where \(a \) is an arbitrary element of \( \Sigma \).
2. If \( \mathfrak{M} \) contains \( f \) and \( g, \) then \( \mathfrak{M} \) also contains the difference \( f - g; \) so if \( \mathfrak{M} \) contains \( f, \) then \( \mathfrak{M} \) also contains \( nf \) for all integers \( n. \)^[7]

This definition of an ideal seems to have originated with her paragon Dedekind in the 1870s.^[8] She thinks of an ideal as a kind of number, motivated by the identification of a specific integer \( n \) in the integers \( \mathbb{Z} \) with the ideal it generates, namely, the set of all integers divisible by \( n, \) denoted by \( (n) \). Examples typically have \( n > 0, \) but this needn't be the case, the convention justified by the fact that \( (n) = (m) \) if and only if \( \ n = \pm m. \) She uses terms and a notation rooted in this comparison. As with Gauss and down to this day, \( 10 \equiv 0 \hspace{0em} {\pmod{2}} \) means \( 10 = 10 - 0 \) is divisible by \( 2. \) In recent times, this would be denoted by \( 10 \in (2); \) that is, \( 10 \) is in the ideal generated by \( 2, \) but Noether retains the Gaussian notation for ideals generally: she writes \( f \equiv 0 (\mathfrak{M}) \) for \( f \in \mathfrak{M}, \) eliding the "mod". So too, \( \mathfrak{N} \subseteq \mathfrak{M} \) is denoted by \( \mathfrak{N} \equiv 0 (\mathfrak{M}) \) and expressed as \( \mathfrak{N} \) is divisible by \( \mathfrak{M}. \)

When she says of two ideals \( \mathfrak{A} \) and \( \mathfrak{B} \) that \( \mathfrak{A} \) goes into \( \mathfrak{B}, \) she means that \( \mathfrak{A} \) divides \( \mathfrak{B}, \) that is, that \( \mathfrak{B} \subseteq \mathfrak{A}. \) This is confusing at first for the modern reader but perfectly sensible when translated to the integers:

\[ (24) \subseteq (6) \subseteq(2) \text{ in } \mathbb{Z} \]

is synonymous with:

\[ 2 \; | \; 6 \; | \; 24 \]

because every multiple of \( 24 \) is a multiple of \( 6 \) and every multiple of \( 6 \) is a multiple of \( 2. \) We're so used to thinking of a divisor as something smaller, but in ideal theory the divisor is larger. This notion of divisibility for ideals goes back to Dedekind in the 1870s and before that to Kummer in the 1840s.^[9] "The remaining familiar notions also remain valid, word for word," she says, continuing:

By the greatest common divisor \( \mathfrak{D} = (\mathfrak{A}, \mathfrak{B}) \) of two ideals \( \mathfrak{A} \) and \( \mathfrak{B} \), we understand this to be all elements which are expressible in the form \( a + b, \) where \( a \) is an element of \( \mathfrak{A} \) and \( b \) is an element of \( \mathfrak{B}; \mathfrak{D} \) is also itself an ideal.^[10]

This too makes sense when you remember that the common multiples of two integers \( a \) and \( b \) consist exactly of the multiples of their greatest common divisor; the concept extends directly to more than two ideals. An equivalent definition of the greatest common divisor \( d \) of two integers \( a \) and \( b \) in \( \mathbb{Z} \) is that \( d = \text{ gcd}(a,b) \) is the positive integer \( d \) that divides both \( a \) and \( b \) and which is divided by all common divisors of \( a \) and \( b. \) Translating that into the Kummer-Dedekind notion of divisibility employed by Noether: the greatest common divisor \( \mathfrak{D} \) of two ideals \( \mathfrak{A} \) and \( \mathfrak{B}, \) denoted \( (\mathfrak{A}, \mathfrak{B}), \) is the ideal \( \mathfrak{D} \) containing both \( \mathfrak{A} \) and \( \mathfrak{B} \) and which is contained in every ideal containing both \( \mathfrak{A} \) and \( \mathfrak{B}. \) Or equivalently: the greatest common divisor of ideals \( \mathfrak{A} \) and \( \mathfrak{B} \) is the smallest ideal \( \mathfrak{D} \) containing them both:

\begin{align}
\text{gcd}(4, 6) &= 2, \text{ as numbers in } \mathbb{Z},\\
\text{gcd}((4), (6)) &= ((4), (6)) = (4) + (6) = (2), \text{ as ideals in the ring } \mathbb{Z}.
\end{align}

The least common multiple \( m \) of two integers \( a \) and \( b \) in \( \mathbb{Z} \) is the positive integer \( m = \text{ lcm}(a,b) \) that is a multiple of them both and which divides all common multiples of them both. Translating to ideals: the least common multiple \( \mathfrak{M} \) of two ideals \( \mathfrak{A} \) and \( \mathfrak{B}, \) denoted \( [\mathfrak{A}, \mathfrak{B}], \)is the ideal \( \mathfrak{M} \) contained in both \( \mathfrak{A} \) and \( \mathfrak{B} \) and which contains every ideal contained in both \( \mathfrak{A} \) and \( \mathfrak{B}. \) Or equivalently: the least common multiple of ideals \( \mathfrak{A} \) and \( \mathfrak{B} \) is the largest ideal \( \mathfrak{D} \) contained in them both, namely, \( \mathfrak{M} = \mathfrak{A} \cap \mathfrak{B}: \)

\begin{align}
\text{lcm}(4, 6) &= 12, \text{ as numbers in } \mathbb{Z},\\
\text{lcm}((4), (6)) &= [(4), (6)] = (4) \cap (6) = (12), \text{ as ideals in the ring } \mathbb{Z}.
\end{align}

An ideal \( \mathfrak{M} \) is said to have an ideal basis \( f_1, f_2, \ldots, f_\varrho \) if every element \( f \in \mathfrak{M} \) can be expressed as:

\[ f = a_1 f_1 + \cdots + a_\varrho f_\varrho + n_1 f_1 + \cdots + n_\varrho f_\varrho, \]

for some \( a_i \) in the ring and integers \( n_i \) (the terms with the \( n_i \) are unnecessary when the ring has a unit). The shorthand notation is:

\[ \mathfrak{M} = ( f_1, f_2, \ldots, f_\varrho). \]

This is straight from Emmy Noether, who says that she is going to consider only rings satisfying the finiteness condition in Idealtheorie in Ringbereichen, that is, rings in which every ideal has an ideal basis (today "finite basis" is used instead of "ideal basis"). She then states and proves this key theorem for rings satisfying the finiteness condition:

Theorem I^[11] (Theorem of the Finite Chain): If \( \mathfrak{M}_1, \mathfrak{M}_2, \ldots \mathfrak{M}_\nu, \ldots \) is a countably infinite system of ideals in \( \Sigma \) in which each ideal is divisible by the following one, then all ideals after a finite index \( n \) are identical; \( \mathfrak{M}_n = \mathfrak{M}_{n+1} = \ldots. \) In other words: If \( \mathfrak{M}_1, \mathfrak{M}_2, \ldots \mathfrak{M}_\nu, \ldots \) gives a simply ordered chain of ideals such that each ideal is a proper divisor of its immediate predecessor, then the chain terminates in a finite number of steps.

Proof. Let \( \mathfrak{D} = (\mathfrak{M}_1, \mathfrak{M}_2, \ldots \mathfrak{M}_\nu, \ldots) \) be the greatest common divisor of the \( \mathfrak{M}_i, \) itself an ideal and therefore possessing an ideal (finite) basis:

\[ \mathfrak{D} = (f_1, f_2, \ldots, f_k). \]

Each \( f_i \) is in some \( \mathfrak{M}_j, \) and since the \( \mathfrak{M}\)s are contained in each other in an ascending chain, every \( f_i \in \mathfrak{M}_{n} ,\) where \( n \) is the greatest of all the indices \( j. \) All the \( f_i \) are therefore contained in all divisors of \( \mathfrak{M}_{n} \) in the ascending chain, that is, all \( \mathfrak{M}_{s} \) where \( s \geq n, \) which are therefore multiples of \( \mathfrak{M}_{n} \) as well as divisors of it. That is, \( \mathfrak{M}_{s} = \mathfrak{M}_{n} \) for \( s \geq n. \)QED.

Noether says that Dedekind initially stated Theorem I for modules and that her proof and the term "chain" are taken from him, also that Emanuel Lasker had it for polynomial rings. She claims a generality not found in the earlier works though.

Noether's Finite Chain Condition is today called the Ascending Chain Condition (ACC) and she notes that the converse of Theorem I holds as well (if the ACC holds in a ring, then every ideal has a finite basis). Modern terminology is different: \( \mathfrak{M}_j \subseteq \mathfrak{M}_{j+1} \) rather than \( \mathfrak{M}_j \) divides \( \mathfrak{M}_{j+1} \) and \( \mathfrak{D} = \cup \mathfrak{M}_j \) instead of \( \mathfrak{D} \) is the greatest common divisor of the \( \mathfrak{M}_j. \) But what is striking is that proofs of Theorem I till this day follow Noether's logic — that is a long life in the history of mathematics.^[12] Even more important is the enduring value of the concept of the Ascending Chain Condition — Robert Gilmer says that one of Noether's main contributions was "in isolating the condition, recognizing its utility, and defining it in an abstract setting". Rings with the ACC are now called Noetherian, a coinage apparently due to Claude Chevalley in 1943.^[13]

Prime and primary Ideals are central in commutative ring theory:

The term "prime" is from the integers, whose prime ideals are exactly ideals \( (p), \) where \( p \) is a prime number. All ideals in \( \mathbb{Z} \) are of the form \( (m) \) for some integer \( m, \) a fact proven using the division algorithm in \( \mathbb{Z}. \) Let \( p \) be a prime number and assume that \( ab \in (p), \) that is, \( p \; | \; ab. \) This implies that \( p \; | \; a \) or \( p \; | \; b, \) so \( a \in (p) \) or \( b \in (p), \) proving that \( p \) is a prime ideal when \( p \) is a prime number. Conversely, if \( n \) is not a prime number, then there are integers \( 1 < a, b < n \) such that \( n = ab. \) Then \( ab = n \in (n), \) but \( a \not \in (n), b \not \in (n), \) proving that \( (n) \) is not a prime ideal.

Primary ideals in \( \mathbb{Z} \) are of the form \( (p^\kappa), \) where \( p \) is a prime number and \( \kappa = 1, 2, 3, \ldots. \) For suppose \( ab \in (p^\kappa), p \) a prime number, and \( a \not \in (p^\kappa); \) that is, \( p^\kappa \; | \; ab, \) and \( p^\kappa \not | \; a; \). Then the highest power of \( p \) dividing \( a \) is \( p^{\kappa-1}, \) so \( p \) to at least the first power divides \( b, \) that is, \( p \; | \; b, \) and therefore \( p^\kappa \; | \; b^\kappa. \) In other words, \( b^\kappa \in (p^\kappa), \) proving that \( (p^\kappa) \) is a primary ideal in \( \mathbb{Z}. \) To show that they are the only primary ideals in \( \mathbb{Z}, \) suppose that \( (m) \) is an ideal where \( m \) is divided by at least two distinct prime numbers: \( m = p^\lambda q^\mu m', \) where \( p \) and \( q \) are prime and \( \lambda \geq 1, \mu \geq 1. \) Assume further that no power of \( p \) or \( q \) divides \( m'. \) Put \( a = p^\lambda, b = q^\mu m'. \) Then \( ab \in (m) \) and \( a \not \in (m), \) but \( m \) cannot divide any power of \( b \) since the prime number \( p \) divides \( m \) but not \( b. \) That is, \( b^\nu \not \in (m) \) for all \( \nu = 1, 2, 3, \ldots \) proving that the ideal \( (m) \) is not primary.

Noether introduces prime and primary ideals like this for Noetherian rings in Idealtheorie:

Definition III.^[14] An ideal \( \mathfrak{Q} \) is called primary if \( a \cdot b \equiv 0\ (\mathfrak{Q}),\ a \not\equiv 0\ (\mathfrak{Q}) \) implies \( b^{x} \equiv 0\ (\mathfrak{Q}), \) where the exponent \( x \) is a finite number.

The definition can also be restated as follows: if a product \( a \cdot b \) is divisible by \( \mathfrak{Q}, \) then either one factor is divisible by \( \mathfrak{Q} \) or a power of the other is. If in particular \( x \) is always equal to \( 1, \) then the ideal is called a prime ideal.

From the definition of a primary (respectively prime) ideal follows, by virtue of the existence of a basis, the definition using only products of ideals (the product \( \mathfrak{A} \cdot \mathfrak{B} \) of two ideals is understood to mean, as usual, the ideal consisting of the collection of elements \(a \cdot b \) and their finite sums):

Definition IIIa. An ideal \( \mathfrak{Q} \) is called primary if \( \mathfrak{A} \cdot \mathfrak{B} \equiv 0\ (\mathfrak{Q}), \mathfrak{A} \not\equiv 0\ (\mathfrak{Q}) \) necessarily implies \( \mathfrak{B}^{\lambda} \equiv 0\ (\mathfrak{Q}). \) If \( \lambda \) is always equal to \( 1 \), then the ideal is called a prime ideal. For a prime ideal \(\mathfrak{P}, \) it therefore always follows from \( \mathfrak{A} \cdot \mathfrak{B} \equiv 0\ (\mathfrak{P}), \mathfrak{A} \not\equiv 0\ (\mathfrak{P}) \) that \( \mathfrak{B} \equiv 0\ (\mathfrak{P}).\)

The notation and letters have been superseded (those ideals are \( Q, A, B, \) and \( P \)), but the concepts have stood the test of time. She notes that Definition III is contained in Definition IIIa by taking \( A = (a), B = (b) \) as a special case; that is, every ideal primary by IIIa is also primary by III. She proceeds to prove the converse as follows, the notation being mine but the argument hers. Suppose ideal \( Q \) is primary by Definition III and \( A \) and \( B \) are ideals with \( AB \subseteq Q, A \subsetneqq Q. \) Choose \( a \in A, a \not \in Q, \) and let \( B = (b_1, \ldots, b_r). \) Since \(a \cdot B \subseteq Q, ab_i \in Q \) for all \( i. \) Therefore by III, there are natural numbers \( x_i \) such that \( b_i^{x_i} \in Q. \) Suppose:

\begin{align}
b &= f_1b_1 + \cdots + f_rb_r, \hspace{5pt} f_i \in \Sigma,\\
\lambda &= x_1 + \cdots + x_r.
\end{align}

Then \( b^\lambda \) can be expanded by the multinomial theorem and every term in the expansion has some factor \( b_i^\mu, \) where \( \mu \geq x_i. \) That factor and therefore that term are in \( Q, \) so the sum of all the terms is as well; that is, \( b^\lambda \in Q, \) so \( Q \) is primary.

Similarly assume ideal \( P \) is prime according to Definition III, where \( x = 1. \) Let \( A \) and \( B \) be ideals with \( A \cdot B \subseteq P, A \subsetneqq P. \) Choose \( a \in A, a \not \in P. \) Then for any \( b \in B, ab \in P \) and so \( b \in P \) (since \( a \) isn't in \( P \)). In other words, \( B \subseteq P \) as stipulated by IIIa.

Start of Idealtheorie

Idealtheorie starts:

This paper aims to convert the decomposition theorems for the integers or the decomposition of ideals in algebraic number fields into theorems for ideals in arbitrary integral domains (and rings in general).^[15]

In \( \mathbb{Z} \) positive integers \( m \) have a unique prime power factorization up to the order of factors:

\begin{align}
m &= p_1^{\varrho_1} p_2^{\varrho_2} \ldots p_\sigma^{\varrho_\sigma}\\
&= q_1 q_2 \ldots q_\sigma,\\
\end{align}

where the \( q_i = p_i^{\varrho_i} \) are now the focus as the components of the decomposition and have these properties:

1) The \( q_i \) are irreducible in the sense that \( q_i \neq q_j q_k, j \neq i, k \neq i. \)

2) The \( q_i \) are irreducible in the sense that \( q_k \; | \; bq_i \Rightarrow q_k \; | \; b. \)

3) The \( q_i \) are primary as discussed above and maximally so, in that no product of them is primary.

4) Each \( q_i \) is irreducible in the sense that it cannot be written as the least common multiple of two proper divisors.

Converting this to ideals \( Q_i \) in any commutative Noetherian ring (\( Q_i \) playing the role of \( (q_i) \)), any ideal \( M \) can be written:

\begin{align}
M = Q_1 \cap Q_2 \cap \ldots \cap Q_\sigma,
\end{align}

where the \( Q_i \) are primary ideals associated with different corresponding prime ideals \( P_i, \) the number of components and the \( P_i \) being the same for any decomposition. The decomposition is minimal in the sense that no \( Q_i \) contains the intersection of two others. This is the Primary Decompostion Theorem for ideals in Noetherian rings, and is what Emmy Noether proved in Idealtheorie.

The first step is to define the concept of an irreducible ideal, analogous to a prime number in \( \mathbb{Z}: \) An ideal is irreducible if it cannot be written as the least common multiple of two proper factors. In set theoretic terms: an ideal \( C \) is irreducible if \( C = A \cap B \Rightarrow C = A \) or \( C = B. \)

Or as Noether puts it in the subheading of §2 in Idealtheorie: Representation of an ideal as the least common multiple of finitely many irreducible ideals.^[16] She replaced the involved proof in Idealtheorie with a more succinct one in another outstanding paper, "Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionskorpern", published in 1927. Here is the statement there and her proof, intact except for changing it to Theorem II as in Idealtheorie rather than Theorem I as in Aufbau, using Latin letters instead of German ones (\( M \) instead of \( \mathfrak{M} \)), and using intersection instead of least common multiple (\( A \cap B \) instead of \( [A, B] \)):

Theorem II.^[17] Every ideal of [a ring] R can -- assuming the ascending chain condition -- be expressed as the least common multiple of finitely many irreducible ideals, that is, ideals which cannot themselves be expressed as least common multiples of two proper divisors.

For the proof, we show: If Theorem II is not satisfied by an ideal \( M, \) then \( M \) has a proper divisor for which Theorem II is likewise not satisfied; hence an ascending chain is constructed which does not terminate in finitely many steps, contradicting the ascending chain condition. Indeed, \( M \) must be reducible, otherwise \( M = [M] \) would provide the desired expression. If \( M = A \cap B\) then Theorem II cannot be satisfied for \( A \) and \( B \) simultaneously, otherwise a corresponding expression for \( M \) would follow. There are therefore proper divisors of \( M \) for which Theorem II is not satisfied; let \( A_1 \) be the first one in the well-ordering of the ideals. By constructing a proper divisor \( A_2 \) corresponding to \( A_1, \) and generally a proper divisor \( A_{i+1} \) for \( A_i, \) one obtains a well-defined ascending chain which does not terminate in finitely many steps, contrary to the assumption.QED.

Idealtheorie has no mention of the maximal condition, defined in the now canonical way by van der Waerden in Moderne Algebra in 1931:

If the divisor chain condition (ACC) is valid in [ring] \( \mathfrak{o}, \) then in every non-empty set of ideals there is a maximal ideal, i.e., an ideal which is contained in no other ideal of the set.^[18]

The maximal condition in turn implies the ACC. A proof of Theorem II today typically invokes the maximal condition by considering the set \( \Lambda \) of all counterexamples, that is, the set of all ideals that cannot be represented as a finite intersection of irreducible ideals. If \( M \) is a maximal element of \( \Lambda, \) then in particular, it is not irreducible — that is, it is reducible, so \( M = A \cap B, \) where \( A \) and \( B \) are ideals such that \( M \subsetneqq A, \; M \subsetneqq B. \) By the maximality of \( M, \) each of \( A \) and \( B \) can be represented as a finite intersection of irreducible ideals, but then \( M \) can be as well, a contradiction. It follows that \( \Lambda \) is empty — there are no counterexamples, so the theorem is proven.

Noether uses the well-ordering theorem in concert with the ACC to prove Theorem II. The well-ordering theorem stipulates that every collection of sets can be put into an order such that there is a least element — her \( A_1, A_2, \) and so on in the proof which specify one specific path through the lattice of possible proper divisors. The well-ordering theorem is equivalent to each of Zorn's Lemma and the Axiom of Choice, big cannons to bring down something following directly from the ACC in the guise of the maximal condition, as just outlined.

To quote Noether's subheading of §3 of Idealtheorie: Equality of the number of components in two different decompositions into irreducible ideals.

Definition of Reduced Representation (Reduzierte Darstellung) in §2 of Idealtheorie.^[19]

A reduced representation of an ideal \( M \) is a representation \( M = B_1 \cap B_2 \cap \cdots \cap B_k \) in which no component \( A_i \) contains the intersection of all the others, and no component can be replaced by a proper divisor (superset). A representation in which the first of these conditions obtains is called a shortest representation. A representation is reduced with respect to one of its components if that component does not contain the intersection of all the others and that component cannot be replaced by a divisor (superset). In Lemma I in Idealtheorie, Noether uses the ACC to prove that every representation can be replaced by a reduced representation. The first step in proving equality of the number of components is:

Theorem III.^[20] Let the shortest representation \( \mathfrak{M} = [\mathfrak{A},\mathfrak{C}] \) be reduced with respect to \( \mathfrak{C}. \) Then a necessary and sufficient condition for \( \mathfrak{C} \) to be reducible is the existence of two ideals \( \mathfrak{N}_{1} \) and \( \mathfrak{N}_{2} \) which are proper divisors of \( \mathfrak{M} \) such that \begin{equation}{\mathfrak{N}_{1} \equiv 0\ (\mathfrak{A}); \quad \mathfrak{N}_{2} \equiv 0\ (\mathfrak{A}); \quad [\mathfrak{N}_{1}, \mathfrak{N}_{2}] = \mathfrak{M}.}\tag{1}\end{equation}

Proof. \( A \) is the complement of \( C \) in the representation \( M = A \cap C. \) "Shortest representation" means that no component contains the intersection of two others if the representation is written out in full (that is, if \( A \) is expressed as an intersection of components). "Reduced with respect to \( C \)" means that \( C \) cannot be replaced by a divisor (superset) in the representation.

Suppose \( C \) is reducible; that is, \( C = C_1 \cap C_2, \) where \( C \subsetneqq C_1 \) and \( C \subsetneqq C_2. \) Then:

\begin{align}
M = A \cap C = A \cap C_1 \cap C_2 = \underbrace{(A \cap C_1)}_{\large N_1} \cap \underbrace{(A \cap C_2)}_{\large N_2}.
\end{align}

If \( A \cap C_1 = M, \) then the representation would not be reduced with respect to \( C \) (since \( C \subsetneqq C_1 \)). Therefore \( M \subsetneqq A \cap C_1 \) and similarly \( M \subsetneqq A \cap C_2, \) showing that \( N_1 = A \cap C_1 \) and \( N_2 = A \cap C_2 \) satisfy the conditions in (1).

Conversely, suppose ideals \( N_1 \) and \( N_2 \) exist which are proper divisors of \( M \)such that:

\begin{align}
N_1 \subseteq A, \hspace{10pt} N_2 \subseteq A, \hspace{10pt} M = N_1 \cap N_2.
\end{align}

Put

\begin{align}
C_1 = C + N_1, \hspace{10pt} C_2 = C + N_2, \hspace{10pt} C^* = C_1 \cap C_2.
\end{align}

Then \( C \subseteq C_1 \) and \( C \subseteq C_2, \) so \( C \subseteq C^* = C_1 \cap C_2. \) The object is to prove that \( C^* \subseteq C \) as well, so suppose \( f \in C^* \):

\begin{align}
f = c + n_1 = \overline{c} + n_2, \hspace{10pt} c, \overline{c} \in C, \hspace{5pt} n_1 \in N_1, \hspace{5pt} n_2 \in N_2.
\end{align}

Note \( n_1, n_2 \in A. \) Put \( g = c - \overline{c} = n_2 - n_1. \) Then \( g \in C, g \in A, \) so \( g \in A \cap C = M \subseteq N_2. \) Therefore \( n_1 = n_2 - g \in N_1 \cap N_2 = M \subseteq C \) and \( f = c + n_1 \in C. \) It follows that \( C^* \subseteq C \) and therefore \( C^* = C. \)

\( C_1 \) and \( C_2 \) are proper divisors of \( C. \) For suppose \( C_i = (C, N_i) = C. \) Then \( N_i \subseteq C \) and \( N_i \subseteq A, \) so \( N_i \subseteq A \cap C = M. \) Then \( N_i \) is not a proper divisor of \( M, \) contrary to assumption. Therefore \( C_1 \) and \( C_2 \) are proper divisors of \( C, \) which is therefore reducible.QED.

This lemma will also be necessary, proven with "almost identical reasoning" as she says:

Lemma II.^[21] If the ideal \( \mathfrak{C} \) in a shortest representation \( \mathfrak{M} = [\mathfrak{A}, \mathfrak{C}] \) can be replaced with a proper divisor, then \( \mathfrak{C} \) is reducible.

Proof. Let \( M = A \cap C = A \cap C_1, \) where \( C \subsetneqq C_1, \) and set

\begin{align}
C^* = C_1 \cap (A + C).
\end{align}

Clearly \( C \subseteq C^*. \) To prove the inclusion the other way, suppose \( f \in C^*, \) so

\begin{align}
f = c_1 = a + c, \hspace{10pt} c_1 \in C_1, \hspace{5pt} a \in A, \hspace{5pt} c \in C.
\end{align}

\( a = c_1 - c \in C_1 \) since \( C \subseteq C_1, \) so \( a \in A \cap C_1 = M. \) Since \( M \subseteq C, \) this implies that \( a \in C. \) Therefore \( f = a + c \in C \) and so \( C^* \subseteq C. \) It follows that \( C^* = C. \) Furthermore, \( C \subsetneqq A + C, \) because otherwise \( A \subseteq C, \) so \( M = A \cap C \) is not a shortest representation. Therefore

\begin{align}
C = C^* = C_1 \cap (A + C), \hskip{10pt} C \subsetneqq C_1 \hskip{5pt} C \subsetneqq A + C,
\end{align}

so \( C \) is reducible.QED.

Lemma II shows that an irreducible ideal cannot be replaced with a proper divisor in a shortest representation. In particular, if \( M = B_1 \cap B_2 \cap \cdots \cap B_k \) is a shortest representation of \( M \) by irreducible ideals, then the representation must be reduced.

Lemma III.^[22] Let \( \mathfrak{M} = [\mathfrak{B}_1, \ldots, \mathfrak{B}_k] = [\mathfrak{D}_1, \ldots, \mathfrak{D}_l] \) be two different shortest representations of \( \mathfrak{M} \) as the least common multiple of (finitely many) irreducible ideals. Then for every complement \( \mathfrak{A}_i = [\mathfrak{B}_1, \ldots, \mathfrak{B}_{i-1}, \mathfrak{B}_{i+1}, \ldots, \mathfrak{B}_k], \) there exists an ideal \( \mathfrak{D}_j \) such that \( \mathfrak{M} = [\mathfrak{A}_i, \mathfrak{D}_j]. \)

Proof. By the remark immediately above, both representations are reduced. We have:

\begin{align}
M = B_1 \cap \ldots \cap B_k = D_1 \cap \ldots \cap D_l.
\end{align}

Set \( M = D_1 \cap C_1, \; C_1 = D_2 \cap C_{12}, \) and generally \( C_{12 \dots s} = D_{s+1} \cap \ldots \cap D_l \) for \( s < l. \) Then:

\begin{align}
M = A_i \cap M = A_i \cap (D_1 \cap C_1) = \underbrace{(A_i \cap D_1)}_{\large N_1} \cap \underbrace{(A_i \cap C_1)}_{\large N_2}.
\end{align}

Theorem III applies with \( N_1 = A_i \cap D_1, \; N_2 = A_i \cap C_1 \) because \( M = A_i \cap B_i \) is reduced with respect to \( B_i \) and the representation is a shortest one. Because the \( B_i \) are assumed to be irreducible, one of the \( N_i \) must be equal to \( M. \) For \( N_1 = M, D_1 \) is the \( D_j \) promised and the lemma is proven. Otherwise \( N_2 = M, \) so:

\begin{align}
M = N_2 = A_i \cap C_1 = A_i \cap (D_2 \cap C_{12}) = \underbrace{(A_i \cap D_2)}_{\large N_1'} \cap \underbrace{(A_i \cap C_{12})}_{\large N_2'}.
\end{align}

Just as before, one of the \( N_i' \) must equal \( M. \) Continuing in this way, it follows either that \( M = A_i \cap D_j, \) where \( j < l, \) or that \( M = A_i \cap C_{12 \dots l-1}. \) The lemma follows in either case considering that \( C_{12 \dots l-1} = D_l. \)QED.

Lemma III leads in short order to:

Theorem IV.^[23] For two different shortest representations of ideals as the least common multiple of irreducible ideals, the number of components is the same.

Proof. Assume we have two different shortest representations:

\begin{align}
M = B_1 \cap \ldots \cap B_k = D_1 \cap \ldots \cap D_l.
\end{align}

Apply lemma III with \( i = 1: \)

\begin{align}
M = A_1 \cap B_1 = A_1 \cap D_{j1} = D_{j1} \cap B_2 \cap \ldots \cap B_k,
\end{align}

leading to:

\begin{equation}{M = D_{j1} \cap B_2 \cap \ldots \cap B_k = D_1 \cap D_2 \cap \ldots \cap D_l.}\tag{2}\end{equation}

Note that \( D_{j1} \) cannot equal any of \( B_2, B_3, \ldots B_k, \) otherwise \( M = B_1 \cap \ldots \cap B_k \) would not be a shortest representation, so both intersections in (2) are shortest representations. Apply lemma III again to arrive at:

\begin{equation}{
M = D_{j1} \cap D_{j2} \cap B_3 \cap \ldots \cap B_k = D_1 \cap D_2 \cap \ldots \cap D_l.
}\tag{3}\end{equation}

If \( D_{j1} = D_{j2}, \) then

\begin{align}
M = D_{j1} \cap B_3 \cap \ldots \cap B_k,
\end{align}

so the representation of \( M \) on the left of (2) would not be a shortest one. Therefore \( D_{j1} \neq D_{j2}. \) For the same reason, \( D_{j2} \) cannot equal any of \( B_3, B_4, \ldots B_k. \) In short, both intersections in (3) are shortest representations. Continue in this fashion to replace the \( B \)s with \( D \)s, always possible as long as there is a \( D \) left on the right side of equations like (3). This shows that the \( B \)s will be exhausted before the \( D \)s are; that is, \( k \leq l. \) By the symmetry of the situation, \( l \leq k \) and so \( k = l. \)QED.

Replacement theorems like Lemma III and Theorem IV have a long lineage in linear algebra, where they are used to prove that all bases of a vector space have the same size. A key result in this vein is the Steinitz replacement theorem, also known as the Steinitz exchange lemma proven by Ernst Steinitz in 1913^[24]:

Let \( V \) be a vector space which is spanned by \( n \) elements. If \( V \) contains \( r \) linearly independent elements \( v_1, v_2, \ldots, v_r, \) there is a spanning set of \( V \) consisting of \( n \) elements and containing the \( v_i, \; 1 \leq i \leq r. \) In particular, a vector space spanned by \( n \) elements cannot contain more than \( n \) linearly independent elements.

Steinitz developed the abstract theory of fields in his pivotal 1910 paper "Algebraische Theorie der Körper" (Algebraic Theory of Fields)^[25], which included early discussion of such topics as the characteristic of a field, transcendental extensions, and the algebraic closure of a field.^[26] Peter Roquette writes that "Steinitz's ideas contributed essentially to the shaping of Emmy Noether's concept of mathematics and in particular of algebra", noting that almost all her early papers contain a reference to Steinitz.^[27] In short, she certainly knew of his replacement theorem. Steinitz is known for his abstract approach, but replacement theorems predate him, going back at least to Hermann Grassmann who proved the Steinitz exchange lemma in a more concrete context in 1862.^[28]

Primary ideal \( Q \) and its associated prime ideal \( P .\) Today we say \( P = \text{ rad } Q (P \) is the radical of \( Q ). \)

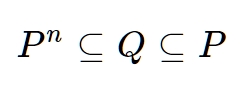
Every primary ideal is associated with prime ideal unique to it. Compare to \( \mathbb{Z}, \) where primary ideal \( (p^n) \) is associated with \( (p). \)

Theorem V.^[29] For every primary ideal \( \mathfrak{Q} \) there exists one, and only one, prime ideal \( \mathfrak{P} \) which is a divisor of \( \mathfrak{Q} \) and a power of which is divisible by \( \mathfrak{Q}; \mathfrak{P} \) shall be referred to as the "associated prime ideal." \( \mathfrak{P} \) is defined as the greatest common divisor of all ideals \( \mathfrak{B} \) with the property that a power of \( \mathfrak{B} \) is divisible by \( \mathfrak{Q}. \) If \( \varrho \) is the smallest number such that \( \mathfrak{P}^\varrho \equiv 0\ (\mathfrak{Q}), \) then \( \varrho \) shall be referred to as the exponent of \( \mathfrak{Q}.\)

Proof. Let \( Q \) be a primary ideal in ring \( R \) and put:

\begin{align}
P = \{ p \in R \; | \; p^n \in Q \text{ for some } n = 1, 2, 3, \ldots \}.
\end{align}

\( P \) is an ideal. For let \( a, b \in P, \; r \in R. \) Then \( a^n \in Q, \; b^m \in Q \) for positive integers \( n \) and \( m. \) In the expansion of \( (a - b)^{n+m-1} \) by the binomial theorem, every term has a factor of \( a^n \) or of \( b^m, \) so that term is an element of \( Q \) and so their sum is as well. That is, \( a-b \in P. \) Also \( (ra)^n = r^na^n \in P. \) It follows that \( P \) is an ideal. And \( P \) is prime ideal. For suppose \( ab \in P. \) Then \( (ab)^k = a^kb^k \in Q \) for some positive integer \( k, \) so \( a^k \in Q \) or some power of \( b^k \) is in \( Q, \) that is, \( (b^k)^j = b^{kj} \in Q, \) for some positive integer \( j. \) That is, \( a \in P \) or \( b \in P, \) showing that \( P \) is a prime ideal.

Let \( D \) be the greatest common divisor of all ideals \( B \) such that \( B^s \subseteq Q \) for some positive integer \( s. \) In other words, \( D \) is the smallest ideal in \( R \) such that \( D^s \subseteq Q \) for some positive integer \( s \) and \( D \) is contained in all every ideal \( B \) such that \( B^t \subseteq Q \) for some positive integer \( t. \) Then \( D = P. \) For if \( B^s \subseteq Q \) for some ideal \( B, \) then \( b^s \in Q, \) so \( b \in P \) for every \( b \in B. \) That is, \( B \subseteq P \) so the greatest common divisor of all such \( B \) is contained in \( P; \) that is, \( D \subseteq P. \) It is also true that \( P^t \subseteq Q \) for some positive integer \( t \) using the multinomial theorem and the fact that \( P \) has a finite basis. Therefore \( P \subseteq D \) as well and \( D = P. \) \( P \) is uniquely defined by these properties. For suppose \( P \) and \( \bar{P} \) are prime ideals such that:

\begin{align}
Q \subseteq P, \; P^s \subseteq Q \text{ for some } s = 1, 2, 3, \ldots,\\
Q \subseteq \bar{P}, \; \bar{P}^t \subseteq Q \text{ for some } t = 1, 2, 3, \ldots
\end{align}

Note that by Definition IIIa, if \( A, B \) and \( P \) are ideals with \( P \) prime, then \( AB \subseteq P \) implies \( A \subseteq P \) or \( B \subseteq P \). Putting \( A = B, \) \( A^2 \subseteq P \) implies \( A \subseteq P, \) and a simple induction establishes that if \( A^n \subseteq P \) for some positive integer \( n, \) then \( A \subseteq P. \) Combining the two equations above results in \( P^s \subseteq Q \subset \bar{P}, \) so \( P \subseteq \bar{P}. \) Similarly \( \bar{P}^t \subseteq Q \subset P, \) so \( \bar{P} \subseteq P. \) Therefore \( \bar{P} = P, \) showing that there is only one prime ideal satisfying these conditions.QED.

The converse of Theorem V is false;^[30] that is, there may be ideals \( M \) and \( P, P \) prime, such that \( P^n \subseteq M \subseteq P, \) but where \( M \) is not primary. Noether gives the example of \( M = (x^2, xy) \) and \( P = (x) \) — in \( \mathbb{Z}[x,y], \) for example, she does not say. \( (x^2) = (x)^2 \subseteq (x^2, xy) \subseteq (x), \) the second inclusion because every term in a polynomial in \( (x^2, xy) \) has a factor of \( x. \) And \( (x) \) is prime, considering that \( (x) \) consists exactly of polynomials \( f(x,y) \) not having a term \( ay^n, \; a \neq 0, \; n \geq 0 \) (\( n = 0 \) is part of this characterization, signifying a nonzero constant \( a \)). For suppose \( f(x,y) \not \in (x), \; g(x,y) \not \in (x). \) Then:

\begin{align}
f(x,y) &= ay^n + \ldots, \hspace{15pt} a \neq 0, \; n \geq 0,\\
g(x,y) &= by^m + \ldots, \hspace{15pt} b \neq 0, \; m \geq 0,
\end{align}

Therefore \( f(x,y) \cdot g(x,y) = aby^{n+m}, ab \neq 0, \; n+m \geq 0. \) That is, \( f(x,y) \cdot g(x,y) \not \in (x), \) so \( P = (x) \) is a prime ideal. Finally, \( M = (x^2, xy) \) is not primary, since \( xy \in M, \) but \( x \) is not in \( M, \) nor is any power of \( y. \) This completes the example.

Nor is it necessarily true that a primary ideal equals a power of its associated prime ideal, as is the case in \( \mathbb{Z}. \) Consider the primary ideal \( Q = (x^2, y) \) and its associated prime \( P = (x,y) \) in \( \mathbb{Z}[x,y], \) for example. \( Q \) consists exactly of polynomials with no constant and no \( x \) term. Let:

\begin{align}
f(x,y) &= a + bx + cy + dx^2 + \ldots,\\
g(x,y) &= a' + b'x + c'y + d'x^2 + \ldots,
\end{align}

where the coefficients are integers, and assume \( f(x,y) \cdot g(x,y) \in Q, \; f(x,y) \not \in Q. \) \( aa' \) is the constant term of \( f(x,y) \cdot g(x,y), \) so \( aa' = 0. \) If \( a \neq 0, \) then \( a' = 0 \) and so every term in \( g^2(x,y) \) is of second or higher degree and therefore \( g^2(x,y) \in Q. \) And if \( a = 0, \) then \( b \) must be nonzero, because if \( a \) and \( b \) were both zero, then \( f(x,y) \in Q, \) which it isn't. \( ab' + a'b = 0 \) because this is the coefficient of the \( x \) term of \( f(x,y) \cdot g(x,y). \) This implies that \( a'b = 0 \) and therefore \( a' = 0, \) so \( g^2(x,y) \in Q \) as before. It follows that \( Q \) is a primary ideal.

Let \( P' \) be the associated prime ideal:

\begin{align}
P' = \{f(x,y) \in \mathbb{Z} \; | \; f^n(x,y) \in Q, \text{ for some } n = 1, 2, 3, \ldots\}.
\end{align}

\( P = (x,y) \) consists exactly of polynomials with no constant term. Therefore the square of a polynomial in \( P \) has only quadratic or greater terms, so it is in \( Q, \) and the original polynomial is in \( P'. \) That is, \( P \subseteq P'. \) Conversely, if a polynomial is not in \( P, \) then it has a nonzero constant term, so all its powers do too. It follows that no power of the original polynomial is in \( Q \) and so the original polynomial is not in \( P'. \) Therefore \( P' \subseteq P \) and \( P = P'. \) In other words, \( P = (x,y) \) is the associated prime ideal of \( Q. \)

Consider \( P^2 = (x^2, xy, y^2), \) consisting exactly of polynomials with quadratic or higher terms. Then:

\begin{align}
P^2 \subsetneqq Q \subsetneqq P,
\end{align}

the inequalities strict because \( y \in Q, \; y \not \in P^2 \) and \( x \in P, \; x \not \in Q. \) Higher powers of \( P \) are contained in \( P^2, \) so \( Q \) cannot equal any power of \( P. \)

Theorem VI.^[31] Every non-primary ideal is reducible; in other words, every irreducible ideal is primary.

Proof. Let \( K \) be a non-primary ideal in ring \( R, \) so by Definition III there exists at least one pair of elements \( a, b \) such that:

\begin{align}
a \cdot b \in K, \hspace{10pt} a \not \in K \hspace{10pt} b^n \not \in K \text{ for } n = 1, 2, 3, \ldots.
\end{align}

Construct the two ideals:

\begin{align}
L_0 = (K, a), \hspace{10pt} N_0 = (K, b).
\end{align}

Then \( K \subsetneqq L_0, \; K \subsetneqq N_0 \) since \( a \not \in K, b \not \in K. \) Also, \( L_0 \cdot N_0 \subseteq K, \) since for typical elements \( k + ra \in L_0, \; k' + r'b \in N_0, \) where \( \; k, k' \in K, \; r, r' \in R: \)

\begin{equation}{(k + ra) \cdot (k' + r'b) = kk' + kr'b + k'ra + rr'ab = k'' + r''ab \in K, \hspace{10pt} k'' \in K, \; r'' \in R,}\tag{4}\end{equation}

considering that \( ab \in K \) by assumption. Put \( K_0 = L_0 \cap N_0 \) and let \( f \in K_0. \) Then \( f = k_1 + a_1b = k_2 + r_2a \) for some \( k_1, k_2 \in K, \; a_1, r_2 \in R. \) Therefore:

\begin{align}
a_1b &= k_2 - k_1 + r_2a \in L_0\\
a_1b^2 &= (a_1b)b \in L_0 \cap N_0 \subseteq K.
\end{align}

That is, \( a_1b^2 \in K. \) There are are two possibilities:

(i) For every \( f \in K_0, \; f = l_0b + k_f \) for some \( l_0 \in L_0, \; k_f \in K. \)

Let \( f \in K_0. \) Since \( l_0 \in L_0 \) and \( b \in N_0, f \in L_0 \cdot N_0 \subseteq K, \) so \( f \in K. \) That is, \( K_0 \subseteq K, \) so \( K = K_0 = L_0 \cap N_0 \) is reducible and the theorem is proven. Otherwise:

(ii) There is an \( f \in K_0 \) such that \( f \neq l_0b + k \) for all \( l_0 \in L_0, \; k \in K. \) Put:

\begin{align}
L_1 = (L_0, a_1) = (K, a, a_1), \hspace{10pt} N_1 = (K, b^2), \hspace{10pt} K_1 = L_1 \cap N_1,
\end{align}

using the \( a_1 \) associated with this \( f \) as stipulated above. Note \( K \subsetneq N_1 \) since \( b^2 \not \in K. \) Since \( ab \in K \) and \( a_1b^2 \in K : \)

\begin{align}
L_1 \cdot N_1 \subseteq K.
\end{align}

It must be the case that \( a_1 \not \in L_0, \) otherwise \( f = l_0b + k_1, \) for \( l_0 = a_1 \in L_0, \) contrary to assumption. Therefore \( L_0 = (K,a) \subsetneqq (K,a,a_1) = L_1. \)

Again there are two possibilities:

(i') For every \( f \in K_1, \; f = l_1b^2 + k_f \) for some \( l_1 \in L_1, \; k_f \in K. \)

Let \( f \in K_1. \) Since \( l_1 \in L_1 \) and \( b^2 \in N_1, f \in L_1 \cdot N_1 \subseteq K, \) so \( f \in K. \) That is, \( K_1 \subseteq K, \) so \( K = K_1 = L_1 \cap N_1 \) is reducible and the theorem is proven. Otherwise:

(ii') There is an \( f \in K_1 \) such that \( f \neq l_1b^2 + k \) for all \( l_1 \in L_1, \; k \in K. \)

For \( f' \in K_1 = L_1 \cap N_1, \) there is some \( s \in R \) such that \( f' = k + sb^2, \; k \in K. \) Let \( a_2 \) be the \( s \) associated with the \( f \) in (2'); that is, \( f = k + a_2b^2, \; k \in K. \) Put

\begin{align}
L_2 = (K, a, a_1, a_2) = (L_1, a_2), \hspace{10pt} N_2 = (K, b^4), \hspace{10pt} K_2 = L_2 \cap N_2.
\end{align}

We have \( ab^4 = (ab) \cdot b^3 \in K, \; a_1b^4 = (a_1b^2) \cdot b^2 \in K, \) and \( a_2b^4 \in K \) as well, since \( a_2b_4 = (a_2b^2) \cdot b^2 \in L_1 \cdot N_1 \subseteq K. \) It follows that \( L_2 \cdot N_2 \subseteq K \) by a calculation like that in (4) since all the key cross products are in \( K. \) \( a_2 \not \in L_1 \) since otherwise \( f = l_1b^2 + k \) with \( l_1 = a_2 \in L_1, \) contrary to assumption. Therefore \( L_1 \subsetneqq (L_1, a_2) = L_2. \)

Continuing in this way, define:

\begin{align}
L_0 &= (K, a), \; L_1 = (L_0, a_1), \; \ldots \; L_m = (L_{m-1}, a_m), \; \ldots,\\
N_0 &= (K, b), \; N_1 = (K, b^2), \; \ldots \; N_m = (K, b^{2^m}), \; \ldots,
\end{align}

where the \(a_i \) are defined so that there exists an \( f \in L_{i-1} \cap N_{i-1} \) such that:

\begin{align}
f = a_i \cdot b^{2^{i-1}} + k, \: k \in K; \; a_i \not \in L_{i-1}.
\end{align}

It holds generally that \( L_i \cdot N_i \subseteq K \) and that \( K \subsetneqq N_i, \; L_{i-1} \subsetneqq L_i, \; K \subsetneq N_i. \) By the ACC, the \( L_i \) stabilize at some point, say at \( L_n. \) So for each \( f \in L_n \cap N_n \) there are \( l_f \in L_n, \; k_f \in K \) such that \( f = l_f \cdot b^{2^n} + k_f. \) It follows that \( K = L_n \cap N_n, \) proving that \( K \) is reducible.QED.

van der Waerden proves that an ireducible ideal is primary.

As so often happens in the history of mathematics, this involved proof was soon replaced by a simpler one. In 1922, soon after Idealtheorie was published, Wolfgang Krull introduced the concept of the quotient of two ideals \( A \) and \( B \) in a ring \( R \)^[32]:

\begin{align}
A:B = \{u \in R \; | \; uB \subseteq A \}.
\end{align}

\( A:B \) is an ideal because for \( u, v \in A:B, \; r \in R, \) \( (u - v)B \subseteq uB - vB \subseteq A \) and \( ru \cdot B = r \cdot uB \subseteq rA \subseteq A. \) In \( \mathbb{Z}, (a) : (b) = (c), \) where \( c \) is the product of the factors of \( a \) which are not also factors of \( b. \) In other words, \( c = a / \text{ gcd }(a, b): \)

\begin{align}
(12) : (2) &= (6)\\
(12) : (4) &= (3)\\
(12) : (8) &= (3)\\
(12) : (5) &= (12).
\end{align}

Here is the streamlined proof of Theorem VI in van der Waerden's Moderne Algebra in 1931^[33]:

Suppose ideal \( M \) in ring \( R \) is not primary, so there are \( a, b \in R \) such that \( ab \in M, a \not \in M, \; b^i \not \in M, \; i = 1, 2, 3, \ldots. \) Define:

\begin{align}
M:b &= \{ u \in R \; | \: ub \in M \},\\
M:b^2 &= \{ u \in R \; | \: ub^2 \in M \},\\
M:b^3 &= \{ u \in R \; | \: ub^3 \in M \},\\
&\vdots
\end{align}

\( ub \in M \) implies \( ub^2 = (ub) \cdot b \in M, \) and so too for the higher powers, so \( M:b \subseteq M:b^2 \subseteq M:b^3 \subseteq \ldots, \) which eventually stabilizes by the ACC. That is, there is a \( k \) such that \( M:b^{k+1} = M:b^k, \) so for this \(k: \)

\begin{equation}{ub^{k+1} \in M \Rightarrow u b^k \in M.}\tag{5}\end{equation}

Put \( A = (M, a), \; B = (M, b^k). \) Since \( a \not \in M, \; b^k \not \in M, \; M \subsetneqq A, \; M \subsetneqq B. \) The object is to prove that \( M = A \cap B. \) To this end, assume \( x \in A \cap B. \) Then:

\begin{align}
x &= m + ra = m' + r'b^k, \text{ for some } m, m' \in M, \; r, r' \in R,\\
xb &= mb + rab = m'b + r'b^{k+1},\\
\end{align}

the second equation resulting from multiplying the first one by \( b. \) \( ab \in M, \) so in this second equation, \( mb, rab, \) and \( m'b \) are all in \( M, \) so \( r'b^{k+1} \in M \) as well. By (5), \( r'b^k \in M, \) so \( x = m' + r'b^k \in M. \) This shows that \( A \cap B \subseteq M \) and so \( M = A \cap B, \) proving that \( M \) is reducible.QED.

The converse of Theorem VI is not true. Noether gives the example of \( Q = (x^2, xy, y^\lambda) = (x^2,y) \cap (x,y^\lambda) \) where \( \lambda \geq 2. \)^[34] Take \( Q = (x^2, xy, y^2) \) in \( \mathbb{Z}[x,y], \) for example. \( Q \) consists of the polynomials \( w(x,y) = dx^2 + exy + fy^2 + \ldots \) with no constant and no linear terms. Put \( A = (x^2, y), \) the polynomials with no constant and no \( x \) term; and \( B = (x, y^2), \) the polynomials with no constant and no \( y \) term. Then \( Q = A \cap B, \) where \( Q \subsetneqq A \) since \( y \in A, y \not \in Q; \) and similarly \( Q \subsetneqq B \) since \( x \in B, x \not \in Q. \) Therefore \( Q \) is reducible. And \( Q \) is primary. For suppose \( u(x,y) \cdot v(x,y) \in Q, \; u(x,y) \not \in Q. \) Let:

\begin{align}
u(x,y) &= a + bx + cy + dx^2 + exy \ldots\\
v(x,y) &= a' + b'x + c'y + d'x^2 + e'xy \ldots,\\
\end{align}

where the coefficients are integers. Suppose \( a \neq 0. \) \( aa' \) must equal zero, because it is the constant term of \( u(x,y) \cdot v(x,y), \) which is in \( Q \) and therefore has constant term zero. Therefore \( a' = 0 \) and so \( v^2(x,y) \in Q. \) On the other hand, if \( a = 0, \) then \( ba' = 0 \) and \( ca' = 0 \) because they are the coefficients of \( x \) and \( y \) respectively of \( u(x,y) \cdot v(x,y). \) But \( b \) and \( c \) can't both be zero, because then \( a = b = c = 0, \) and so \( u(x,y) \in Q, \) which it isn't. It follows that \( a' = 0, \) so \( v^2(x,y) \in Q \) like before. In any case \( v^2(x,y) \in Q, \) and so \( Q \) is primary.

Consider two shortest (therefore reduced) representations of ideal \( M \) as the intersection of irreducible ideals:

\begin{align}
M = B_1 \cap \ldots \cap B_k = D_1 \cap \ldots \cap D_k.
\end{align}

Then the prime ideals associated with the \( B_i \) and the \( D_i \) respectively are the same:

Theorem VII.^[35] For two different shortest representations of an ideal as the least common multiple of irreducible ideals, the associated prime ideals agree, and in fact the same associated prime ideals also occur for every decomposition thereof. The ideals themselves can be paired up in at least one way such that a power of the ideal \( \mathfrak{B}_{i} \) is divisible by the associated \( \mathfrak{D}_{i} \) and vice versa. The numbers of ideals agree by Theorem IV.

Proof. Consider the intermediate representations as in Theorem IV, themselves shortest representations:

\begin{align}
M &= D_1 \cap \ldots \cap D_{i-1} \cap \color{red}{B_i} \cap B_{i+1} \cap \ldots \cap B_k\\
&= D_1 \cap \ldots \cap D_{i-1} \cap \color{red}{D_i} \cap B_{i+1} \cap \ldots \cap B_k\\
\end{align}

They are the same except that the component \( B_i \) has been replaced by \( D_i. \) Let \( \bar{A_i} \) be everything in each of these representations except \( B_i \) and \( D_i \) respectively, so:

\begin{align}
M = \bar{A_i} \cap B_i = \bar{A_i} \cap D_i.
\end{align}

Then:

\begin{align}
\bar{A_i} \cdot B_i &\subseteq \bar{A_i} \cap B_i \subseteq D_i, \hspace{10pt} \bar{A_i} \subsetneqq D_i\\
\therefore B_i^{m_i} &\subseteq D_i, \; \text{ for some positive integer } m_i.
\end{align}

That \(\bar{A_i} \subsetneqq D_i \) follows from the fact that the intermediate representation is a shortest one. The second line follows because \( D_i \) is irreducible and therefore primary. Similarly:

\begin{align}
\bar{A_i} \cdot D_i &\subseteq \bar{A_i} \cap D_i \subseteq B_i, \hspace{10pt} \bar{A_i} \subsetneqq B_i\\
\therefore D_i^{n_i} &\subseteq B_i, \; \text{ for some positive integer } n_i.
\end{align}

Let \( P_i \) be the associated prime ideal of \( B_i \) and \( \bar{P_i} \) the associated prime ideal of \( D_i. \) By Theorem V, there are positive integers \( s_i \) and \( t_i \) such that:

\begin{align}
P_i^{s_i} \subseteq B_i \subseteq P_i,\\
\bar{P_i}^{t_i} \subseteq D_i \subseteq \bar{P_i}.
\end{align}

Taking these last two inclusions to the powers \( m_i \) and \( n_i \) respectively and bringing in the inclusions just above:

\begin{align}
P_i^{m_is_i} \subseteq B_i^{m_i} \subseteq D_i \subseteq \bar{P_i},\\
\bar{P_i}^{n_it_i} \subseteq D_i^{n_i} \subseteq B_i \subseteq P_i.
\end{align}

The first of these inclusions implies that \( P_i \subseteq \bar{P_i} \) because \( \bar{P_i} \) is prime and the second one implies that \( \bar{P_i} \subseteq P_i \) because \( P_i \) is prime. That is, \( \bar{P_i} = P_i. \)QED.

The final goal is close.

Theorem VIII.^[36] Should the primary ideals \( \mathfrak{N}_1, \mathfrak{N}_2, \dots, \mathfrak{N}_{\lambda} \) all have the same associated prime ideal \( \mathfrak{P}, \) then their least common multiple \( \mathfrak{Q} = [\mathfrak{N}_{1}, \mathfrak{N}_{2}, \dots, \mathfrak{N}_{\lambda}] \) is also primary and has \( \mathfrak{P} \) as its associated prime ideal. If conversely \( \mathfrak{Q} = [\mathfrak{N}_{1}, \dots, \mathfrak{N}_{\lambda}] \) is a reduced representation for the primary ideal \(\mathfrak{Q}, \) then all \( \mathfrak{N}_{i} \) are primary and have as their associated prime ideal the associated prime ideal \( \mathfrak{P} \) of \( \mathfrak{Q}. \)

Proof. Assume \( Q = N_1 \cap \ldots \cap N_{\lambda}, \) where each \( N_i \) is primary and has \( P \) as its associated prime ideal. Then \( Q \) is primary with associated prime ideal \( P. \) For consider ideals \( A \) and \( B \) such that:

\begin{align}
A \cdot B \subseteq Q, \hspace{10pt} B^k \subsetneqq Q \text{ for any } k = 1, 2, 3, \ldots.
\end{align}

Then \( B \subsetneq P, \) so \( B^k \subsetneq N_i \) for any \( k = 1, 2, 3, \ldots. \) Consequently \( A \subseteq N_i \) for every \( i, \) since all the \( N_i \) are primary, and therefore \( A \subseteq \cap N_i = Q. \) This proves that \( Q \) is primary. To see that \( P \) is the associated prime ideal of \( Q, \) note that \(P^{r_i} \subseteq N_i \subseteq P \) for positive integers \( r_i \) by Theorem V. So if \( r \) is the largest of the \( r_i, \) then \(P^r \subseteq N_i \subseteq P \) for all \( i. \) It follows that \(P^r \subseteq Q = \cap N_i \subseteq P, \) and therefore that \( P \) is the associated prime ideal of \( Q, \) again by Theorem V.

Conversely, let \( Q = N_1 \cap N_2 \cap \ldots \cap N_\lambda \) be a reduced representation of the primary ideal \( Q, \) where \( P \) is the associated prime ideal of \( Q. \) Assume first that the \( N_i \) are all primary, where \( Q = N_i \cap L_i, L_i \) being the intersection of all the \( N_j \) except \( N_i. \) Let \( P_i \) be the associated prime ideal of \( N_i. \) We have \( L_i \cdot N_i \subseteq N_i \subseteq Q \) and \( L_i \subsetneqq Q \) because the given representation is reduced. Therefore because \( Q \) is primary:

\begin{align}
N_i^{s_i} \subseteq Q, \text{ some } s_i = 1, 2, 3, \ldots
\end{align}

Because \( P_i \) is the associated prime ideal of \( N_i, \) it is also true that:

\begin{align}
P_i^{r_i} \subseteq N_i, \text{ some } r_i = 1, 2, 3, \ldots
\end{align}

Putting these two together:

\begin{align}
P_i^{r_i s_i} \subseteq N_i^{s_i} \subseteq Q.
\end{align}

\( P_i \) being the associated prime ideal of \( N_i \) also implies that:

\begin{align}
Q \subseteq N_i \subseteq P_i.
\end{align}

These last two statements show that \( Q \) is sandwiched between a power of \( P_i \) and \( P_i \) itself, so \( P_i \) is the prime ideal associated with \( Q \) — that is, \( P_i = P. \)

It remains to show that for every reduced representation \( Q = N_1 \cap N_2 \cap \ldots \cap N_\lambda, \) the \( N_i \) are primary. To this end, express each \( N_i \) as an intersection of irreducible ideals \( B \) producing a shortest representation:

\begin{align}
Q = B_1 \cap B_2 \cap \ldots \cap B_m,
\end{align}

where each \( B_j \) is irreducible and therefore primary. Since \( Q \) and all the \( B_j \) are primary, the part of the proof immediately above shows that every \( B_j \) has \( P, \) the associated prime ideal of \( Q, \) as its associated prime ideal. Each \( N_i \) is an intersection of some of the \( B_j \):

\begin{align}
N_i = B_{k_1} \cap B_{k_2} \cap \ldots \cap B_{k_i},
\end{align}

where each \( B \) is primary and has \( P \) as its associated prime ideal, so by the first part of the theorem, their intesection intesection \( N_i \) is primary and has \( P \) as its associated prime ideal.QED.

Primary Decomposition.

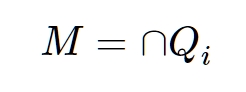
A shortest representation \( M = Q_1 \cap Q_2 \cap \ldots \cap Q_n \) is called the least common multiple (intersection) of maximal primary ideals if all the \( Q \) are primary but the intersection of two \( Q_i \) is no longer primary. There is at least one such representation. To see this, start with a representation by irreducible ideals, each of which is necessarily primary. If any pair of primary ideals in this representation is primary, that pair can be replaced by its intersection, reducing the number of ideals by one. Continuing in this way a finite number of times produces a representation by maximal primary ideals. Such a representation is reduced and every reduced representation representation arises through maximal primary ideals in this way.

Theorem IX.^[37] For two reduced representations of an ideal as the least common multiple of maximal primary ideals, the numbers of components and the associated prime ideals (which are all different from each other) are the same. In other words, each \( \mathfrak{Q} \) can be uniquely associated with a \( \bar{\mathfrak{Q}} \) so that a power of \( \mathfrak{Q} \) is divisible by \( \bar{\mathfrak{Q}}, \) and vice versa. The \( \mathfrak{Q} \) and \( \bar{\mathfrak{Q}} \) have the property of irreducibility with respect to the decomposition into maximal primary ideals.

Proof. Assume we have two different reduced representations of ideal \( M \) by maximal primary ideals:

\begin{equation}{
M = Q_1 \cap \ldots \cap Q_n = \bar{Q}_1 \cap \ldots \cap \bar{Q}_m.
}\tag{6}\end{equation}

Each \( Q_i \) and \( \bar{Q}_j \) can be represented as an intersection of irreducible and therefore primary ideals:

\begin{align}
Q_i = \cap B_{i,s}, \hspace{10pt} \bar{Q}_j = \cap D_{j,t},
\end{align}

where every \( B \) and \( D \) is primary, leading to representations for \( M: \)

\begin{align}
M = \bigcap_{i,s} B_{i,s} = \bigcap_{j,t} D_{j,t}.
\end{align}

By Theorem VII, the number of components and the associated prime ideals are the same in this last representation. Applying Theorem VIII to \( Q_i = \cap B_{i,s}, \) all the \( B_{i,s} \) have the same associated prime ideal \( P_i, \) and the \( P_i \) are all different. Therefore \( n, \) the number of the \( Q_i, \) equals the number of associated prime ideals of all the \( B_{i,s}. \) Similarly \( m, \) the number of the \( \bar{Q}_j, \) equals the number of associated prime ideals of all the \( D_{j,t}. \) Therefore by Theorem VII, \( n = m \) and the associated prime ideals in each representation in (6) is the same and the primary ideals \( Q_i \) and \( \bar{Q}_j \) can be paired so that a power of \( Q_i \) is contained in \( \bar{Q}_j \) and vice versa.QED.

By way of example, consider these two decompositions of \( M = (x^2, xy) \) in \( \mathbb{Z}[x,y]: \)

\begin{align}
M = (x^2, xy) = \underbrace{(x)}_{\large Q_1} \cap \underbrace{(x^2, xy, y^2)}_{\large Q_2} = \underbrace{(x)}_{\large \bar{Q}_1} \cap \underbrace{(x^2, y)}_{\large \bar{Q}_2}
\end{align}

All these ideals were discussed above after Theorems V and VI, where it was shown that \( M \) is not primary, but the four \( Q \)s are (\( Q_1 = \bar{Q}_1 = (x) \) is actually prime). These ideals can be characterized as follows, where \( y^0 = \) a constant is considered to be a power of \( y: \)

• \( M = (x^2, xy): \) polynomials with no term that is a power of \( y \) and no \( x \) term

• \( Q_1 = \bar{Q}_1 = (x): \) polynomials with no term that is a power of \( y \)

• \( Q_2 = (x^2, xy, y^2): \) polynomials with no constant or linear terms

• \( \bar{Q}_2 = (x^2, y): \) polynomials with no \( x \) term and no constant

It follows that \( Q_1 \cap Q_2 \) consists exactly of polynomials with no term that is a power of \( y \) and no \( x \) term, that is, \( Q_1 \cap Q_2 = M, \) and similarly \( \bar{Q}_1 \cap \bar{Q}_2 = M. \) Since neither \( Q_1 \cap Q_2 \) nor \( \bar{Q}_1 \cap \bar{Q}_2 \) is primary, we have two maximal primary decompositions. And they are different since \( y \in \bar{Q_2}, \) but \( y \not \in Q_2. \) The associated prime ideal of \( Q_1 \) and \( Q_2 \) is \(P_1 = (x). \) It was shown above after Theorem V that the the associated prime ideal of \( \bar{Q}_2 \) is \(P_2 = (x, y), \) and since \( P^2_2 \subseteq \bar{Q}_2 \subseteq P_2, \) Theorem V says that \( P_2 \) is also the associated prime ideal of \( \bar{Q_2}. \)

Emmy Noether

Theorem IX is the crowning glory of Idealtheorie, that every ideal in a Noetherian ring can be written as an intersection of maximal primary ideals; while the primary ideals may vary in different representations, the number of primary ideals and their associated prime ideals are always the same. Emmy Noether was thinking about these matters exactly one hundred years ago as she prepared Idealtheorie for publication in January 1921. Many of these proofs were streamlined over the years, often quickly — by Krull, by herself, and especially by van der Waerden. All the same, her results and methods have stood the test of time. Especially her methods, establishing the new abstract approach once and for all in a way that was immediately seen as important and worthy of deep study and emulation.

Idealtheorie is one of the great, trail-blazing works of mathematics in the twentieth century; about half of it is taken up here. I've tried to recapitulate it faithfully, the main changes being to substitute Roman letters for German and intersection for the least common multiple — \( Q_1 \cap Q_2 \cap \ldots \cap Q_n \) for \( [\mathfrak{Q}_1, \mathfrak{Q}_2, \ldots, \mathfrak{Q}_n], \) for example.

No doubt mathematical research over the last hundred years would have proceeded roughly as it has were she never to have lived, but she crystallized the new approach, accelerated its adoption, and sure-handedly laid down an agenda that has been fruitfully executed since the day she set her ideas to paper.

Mike Bertrand

May 23, 2020

Acknowledgements: The foremost debt is to the great Emmy Noether, but also to those who followed in her footsteps and refined her work, B. L. van der Waerden in particular. This project would not have been possible without Daniel Berlyne's English translation of Idealtheorie from 2014. Daniel also translated a key passage from Noether's 1927 paper Aufbau for me (see Theorem II above). Professor Don Passman read parts of this paper, saved me from some egregious errors, and made a number of helpful suggestions; I appreciate his kindness and patience for this journeyman effort.

^ 1. Emmy Noether's dates are 1882 - 1935. Her father Max Noether (1844 - 1921) was a leading German mathematician and founder of algebraic geometry, a subject revolutionized by his daughter Emmy Noether.

^ 2. B. L. van der Waerden uses this tribute of Emmy Noether to Dedekind as an epigram at the start of his reminiscence "On the Sources of My Book Moderne Algebra", Historia Mathematica, 2 (1975), pp. 31-40. The highly influential Moderne Algebra, originally published in German in 1930-1931, organized and presented Emmy Noether's thought to the world.

^ 3. See Modern Algebra, Volume I, Chapter III, §11, "Rings", p. 32 in the 1949-1950 English edition.

^ 4. "Idealtheorie in Ringbereichen" (Ideal Theory in Ring Domains), by Emmy Noether, Mathematische Annalen, 83 (1) (1921), pp 24–66. The second link is Daniel Berlyne's English translation from 2014. Idealtheorie is discussed by Robert Gilmer in "Commutative Ring Theory", pp. 131-143 in Emmy Noether: A Tribute to Her Life and Work, edited by James K. Brewer and Martha K. Smith, Marcel Dekker (1981), ISBN 0-8247-1550-0. Leo Corry also takes up Idealtheorie in Modern Algebra and the Rise of Mathematical Structures, 2nd revised edition, Birkhäuser (2004), ISBN 3-7643-7002-5, pp. 225-237.

^ 5. Gilmer, "Commutative Ring Theory", pp. 131-132.

^ 6. Idealtheorie, p. 29; English translation, p. 7.

^ 7. Idealtheorie, p. 30; English translation, p. 7.

^ 8. Labyrinth of Thought: A History of Set Theory and its Role in Modern Mathematics, by José Ferreirós, Birkhäuser Verlag (1999), ISBN 0-8176-5749-5, p. 106.

^ 9. "Dedekind's 1871 version of the theory of ideals", translation and introduction by Jeremy Avigad, March 19, 2004. See pp. 7-8 of the introduction for "the Dedekind-Kummer notion of divisibility".

^ 10. Idealtheorie, p. 30; English translation, p. 7.

^ 11. Idealtheorie, p. 30-31; English translation, p. 8.

^ 12. For a proof essentially identical to Noether's in a widely used current textbook, see Abstract Algebra, 3rd ed., by David S. Dummit and Richard M. Foote, John Wiley and Sons, Inc. (2004), ISBN 978-0-471-43334-7, pp. 458-459.

^ 13. Gilmer, "Commutative Ring Theory", p. 133, for the quote and the origin of the term "Noetherian". For the latter, he cites “On the Theory of Local Rings,” by Claude Chevalley, Annals of Mathematics, 44 (1943), pp. 690-708.

^ 14. Idealtheorie, p. 37; English translation, p. 16.

^ 15. Idealtheorie, p. 25; English translation, p. 2.

^ 16. Idealtheorie, p. 31; English translation, p. 9.

^ 17. "Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionskorpern" (Abstract Structure of the Ideal Theory in algebraic Number and Function Fields), by Emmy Noether, Mathematische Annalen, 96 (1) (1927), pp 26–61. Thanks to Daniel Berlyne for translating the theorem and proof as given here.

^ 18. Moderne Algebra. Unter Benutzung der Vorlesungen von E. Artin und E. Noether, by B. L. van der Waerden, Verlag Julius Springer (2 volumes, 1930-1931). English translation: Modern Algebra. In part a development from lectures by E. Artin and E. Noether (translated from the 2nd German edition by Fred Blum (Vol. I) and Theodore J. Benac (Vol II), with revisions and additions by the author), Ungar (1949-1950). For the maximal condition, see Vol II, § 84, p. 22.

^ 19. Idealtheorie, p. 31-32; English translation, p. 9.

^ 20. Idealtheorie, p. 34; English translation, p. 12.

^ 21. Idealtheorie, p. 35; English translation, p. 13.

^ 22. Idealtheorie, p. 35; English translation, p. 14.

^ 23. Idealtheorie, p. 36; English translation, p. 14.

^ 24. "Bedingt konvergente Reihen und konvexe Systeme" (Conditionally convergent series and convex systems), by Ernst Steinitz, Journal für die reine und angewandte Mathematik (Crelles Journal), 143 (1913), pp. 128–175.

^ 25. "Algebraische Theorie der Körper" (Algebraic Theory of Fields), by Ernst Steinitz, Journal für die reine und angewandte Mathematik (Crelles Journal), 137 (1910), pp. 167-308.

^ 26. A History of Abstract Algebra, by Israel Kleiner, Birkhäuser (2007), ISBN 978-0-8176-4684-4, p. 75.

^ 27. "In Memoriam Ernst Steinitz (1871-1928)", by Peter Roquette, Journal für die reine und angewandte Mathematik (Crelles Journal), 648 (2010), pp. 1-11. See p. 1 for quote and further discussion. The article is online here.

^ 28. "Hermann Grassmann and the Creation of Linear Algebra", by Desmond Fearnley-Sander, The American Mathematical Monthly, vol. 86, 1979, pp. 809-817. See p. 811 for statement that Grassmann proved the Steinitz Exchange Theorem, as Fearnley-Sander calls it. The article is online here.

^ 29. Idealtheorie, p. 39; English translation, p. 18.

^ 30. This counterexample and the next one are footnotes 17 and 18 in Idealtheorie, p. 39; English translation, p. 18.

^ 31. Idealtheorie, p. 39; English translation, p. 19.

^ 32. "Algebraische Theorie der Ringe I", by Wolfgang Krull, Mathematische Annalen 88 (1922), pp. 80-122. See p. 83 for the ideal quotient \( A : B. \)

^ 33. B. L. van der Waerden, Moderne Algebra. The screen shot and proof of Theorem VI are from Volume II, §87, "The General Decomposition Theorem", p. 31.

^ 34. Idealtheorie, p. 39; English translation, p. 19.

^ 35. Idealtheorie, p. 41; English translation, p. 21.

^ 36. Idealtheorie, p. 42; English translation, p. 22.

^ 37. Idealtheorie, p. 44; English translation, p. 24.