We want to prove that \( \sqrt{2} \) is irrational. That is equivalent to saying that the side and diagonal of a square are incommensurable — that is, their ratio cannot be expressed as the ratio of two whole numbers. The
canonical proof by contradiction, well known by Aristotle's time (384-322 BC), proves that commensurability implies that "odd become equal to even numbers"
in his words. Maybe that's how the Pythagoreans proved it, virtual numerologists that they were.
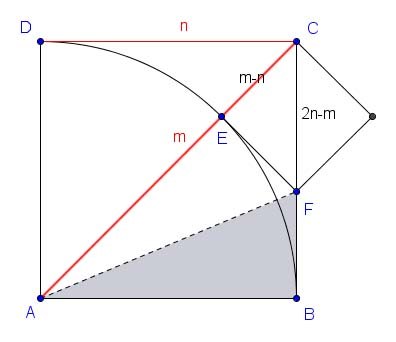
Here is a geometric proof though, also proceeding by contradiction. Suppose that a square's side and diagonal are commensurable with the side's length n and its diagonal m, both whole numbers. Draw a circular arc centered at A, traversing the square from B to D. Obviously \( CE = m-n \), where E is the intersection of arc and diagonal.
Draw the tangent to the arc at E, extending it out to where it intersects BC at F. CEF is an isosceles right triangle — reflect it around its hypotenuse CF to make the smaller square at the upper right of the figure. Right triangles ΔABF (in gray) and ΔAEF are congruent, because they share a hypotenuse and their longer legs both equal n. Therefore \( BF = FE = EC = m-n \) and \(CF = n - (m-n) = 2n-m \).
In other words, the smaller square has side \( m-n \) and diagonal \( 2n-m \). But:
\[ 0 < m - n < n, \hspace{10pt} \text{and} \hspace{10pt} 0 < 2n - m < m. \]
The smaller square has integer-length side and diagonal that are strictly less than those of the original square, but not zero. The same construction can be applied to the second square to derive a still smaller one, and this can go on indefinitely; but that cannot be, because eventually the whole numbers greater than zero run out. Therefore the original assumption is untenable, that the side and diagonal of a square can be in the ratio of two whole numbers.