Rigid Motions of the Dodecahedron

Think of a square in the plane and how it can be rotated around its center to coincide with its original position. There are four rotations altogether — 90°, 180°, 270°, and 360° clockwise, the last bringing the square back to its original configuration. You wouldn't even know the square had been moved unless the corners were somehow distinguished. Starting at the upper left, number the corners 1, 2, 3, 4 in clockwise fashion in order to track the rotations, so that a 90° rotation is identified with the cyclic permutation \( (1 2 3 4) \). In essence, you're rotating around a z axis perpendicular to the plane through the center of the square. You can also rotate around an x, or horizontal, axis through the center of the square. The square comes out of the plane, but is pinned at the middles of the left and right edges as it rotates around that axis through space by 180° — the result is the same whichever way the rotation proceeds, the permutation \( (1 4) (2 3) \). There is a similar vertical rotation, and rotations around each diagonal. These eight rotations form a group, the rigid motions of the square, and the same can be done for any regular polygon. These are the dihedral groups, \( D_4 \) in the case of the square. \( D_n \) has \( 2n \) elements and these groups are nice concrete examples of finite groups.
This can be done with the Platonic solids also — the regular tetrahedron, cube, octahedron, icosahedron, and dodecahedron. The group of rigid motions of the tetrahedron is \( A_4 \), the rigid motions of the cube \( S_4 \). These aren't too hard to work out. In the case of the cube, you can associate each rigid motion with a permutation of the cube's four main diagonals. The regular octahedron is dual to the cube — each has as many vertices as the other had edges, so the centers of the faces of a cube constitute the vertices of a regular inscribed octagon and the rigid motions of each are identified with each other. The icosahedron and dodecahedron are dual in the same way, so it's a matter of taste which figure is examined, their rigid motions are the same.
This subject is steeped in history. The term Platonic solid derives from Plato's ruminations in The Timaeus, where he identifies the tetrahedron, octahedron, icosahedron, and cube with fire, air, water, and earth, respectively, saying of the dodecahedron:
There was yet a fifth combination which God used in the delineation of the universe.
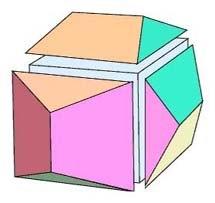
The capstone of Euclid's Elements is the inscription of a regular dodecahedron in a sphere (Book XIII, Proposition 17). Interestingly, he builds little tents on top of the faces of the inscribed cube such that the pentagonal diagonals coincide with the edges of the cube, as suggested in this model. There are five such cubes, considering that (12 pentagonal faces) x (5 diagonals / pentagon) = 60 = (5 cubes) x (12 edges per cube), where every pentagonal diagonal is the edge of a cube. One way of looking at the rigid motions of the dodecahedron is to identify each with a permutation of the five cubes.
In 1856, William Rowan Hamilton described this group in what may be the first group presentation:
\[ {\iota^2 = \kappa^3 = \lambda^5 =1}, \hspace{8pt} {\lambda = \iota \kappa}. \]
He noted that \( {\kappa \iota} \neq {\iota \kappa} \), because otherwise \( \kappa = { \iota \kappa \iota} \), and so:
\[ \lambda^6 = {\iota \kappa \cdot \iota \kappa \cdot\iota \kappa \cdot\iota \kappa \cdot\iota \kappa \cdot\iota \kappa} = {\iota \kappa \iota \cdot \kappa \cdot \iota \kappa \iota \cdot \kappa \cdot \iota \kappa \iota \cdot \kappa} = \kappa^6 = 1. \]
Together with \( \lambda^5 = 1 \), this implies \( \lambda = 1 \), which won't do. Hamilton's brief note is titled Memorandum respecting a new System of Roots of Unity, which is exactly what those symbols are. He drew the analogy with his beloved quaternions and their non-commutative units \( i, j, k \), roots of \( -1 \) in that case.

In 1884, Felix Klein connected the rigid motions of the icosahedron with solving the quintic equation. His seminal book, based on earlier work of Hermite, Kronecker, and Brioschi, is titled Lectures on the Ikosahedron and the Solution of Equations of the Fifth Degree[1]. Here is a nice recapitulation by Oliver Nash, with great references at the bottom. Klein writes as follows towards the start of his account:
But — and this must be emphasised from the first — it is not actually the figures themselves here enumerated which, in the following pages, form the object of our consideration, but rather those rotations or reflexions, or, shortly, those elementary geometrical operations by which the said figures coincide with themselves. The figures are for us only the material by means of which we survey the totality of certain rotations or other deformations. Therefore the individual regular solids will for us be inseparably connected with their polar figures, which, like themselves, remain unaltered by these operations. In this sense the octahedron belongs to the cube whose summits cor respond to the mid-points of the sides of the octahedron, the ikosahedron to the pentagon-dodekahedron, which has an analogous position.\[ \cdots \]The rotations which bring one of the regular solids into coincidence with itself collectively form a group.
For it is clear that any two rotations of this kind, applied one after another, generate again a rotation of the same nature.
If this seems routine today, it is because Klein's prescient approach became canonical virtually from the moment he wrote these words. Klein teases out the structure of the group early in the work and I propose to follow his lead, denoting the rigid motions of the dodecahedron by the group \( \mathcal{G} \). This book exemplifies his celebrated Erlangen Program[2] connecting group theory and geometry and shows its efficacy in addressing other problems of great interest to mathematicians like solving the quintic. Foremost authority Hans Wussing says that "Klein's interest in the group-theoretic treatment of symmetries of regular polyhedra coincided with the creation of the Erlangen Program"[3] (p. 198), and that:
Besides [Camille] Jordan, it was essentially only Klein who had attained, and suitably emphasized, a view of the isomorphism of certain permutation groups and certain groups of symmetries of regular polyhedra — an idea pointing toward the future abstract group concept.
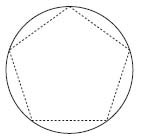
Klein recommends building a model like the one shown above to start understanding the group. I printed out twelve figures like shown here, pentagons inscribed in a circle. I found old file folders perfect for the task, providing a little firmness but feeding through my cheap printer (barely). Then cut out the circles and score with a razor blade along the dashed lines for easy bending. Use a glue stick to glue the little extending tabs together so they fit inside the dodecahedron under construction. My circles were ~\( 4 {1 \over 2} \)" in diameter, pentagon side ~\( 2 {5 \over 8} \)", leading to a dodecahedron about 6" tall (perpendicular distance between opposite faces).
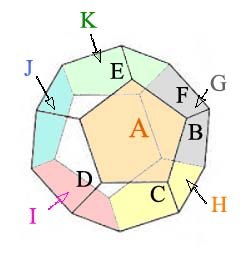
A rigid motion of the dodecahedron can be considered as a permutation of the six pairs of opposite faces (hat tip to Lorraine Foster[4] for the idea). Such a pair of faces will stay opposite each other even after a rigid motion, though they generally map to another pair. The physical model has the faces labelled with letters A through L and the purpose of the diagram here is to show the arrangement of all twelve. Position face A on top, it's colored orange. When looking down at the figure from above, you can see faces B through F each dropping down from face A and connected to it by a common edge — they proceed around face A in a clockwise fashion, are not colored, and are labeled B to F in black. The colored faces are the ones underneath the figure, out of sight. They are labelled G through K, also proceeding clockwise around face A. The face on the bottom, opposite A, is face L (it is the white face in the diagram, label L not shown). Face L on the bottom has a common edge with each of the out-of-sight colored faces G through K.
So the pair of faces A and L is considered as a single object AL, or just A. The other objects are BJ = B, CK = C, DG = D, EH = E, and FI = F. Drop a perpendicular through the center of face A; it will go through the center of the opposite face L also. Rotate the entire figure around that axis by 72° in a clockwise fashion. That's a rigid motion, since the figure coincides with itself after the motion is completed (let's start using rotation instead of rigid motion). Of course faces have been rearranged, that's the point! Face A maps to itself though and face L to itself, so A → A in the abstraction (there are rotations where A and L are exchanged, but that's still considered to be A → A in the abstraction). All the face pairs in this rotation are mapped as follows:
\[ FA1 = \begin{pmatrix}
A \ B \ C \ D \ E \ F \\
A \ C \ D \ E \ F \ B
\end{pmatrix} = (B \ C \ D \ E \ F). \]
More properly, pair BJ maps to pair CK, but we'll just say B maps to C. The notation on the right is standard for indicating a cycle, a 5-cycle in this case. FA1 is my notation for this rotation, F indicating a face rotation, one around the perpendicular axis through the center of the face, A being the face here; there are four such rotations in all, through 72°, 144°, 216°, and 288°.
Since there are six face pairs, there are 24 face rotations of the type just discussed. For example:
\[ FC3 = \begin{pmatrix}
A \ B \ C \ D \ E \ F \\
F \ D \ C \ E \ A \ B
\end{pmatrix} = (A \ F \ B \ D \ E). \]
They are all 5-cycles and each group of four for a given face forms a cyclic subgroup, together with the identity. Next is a set of edge rotations. The edges come in pairs too, each pair being parallel and making a planar rectangle. The physical model above shows a rod through the middle of the edge connecting faces A and C; it goes through the model and comes out at the middle of the opposite edge. Rotating around the rod by 180° provides another rotation. The two parallel edges map to themselves, their endpoints being exchanged. It's clear that faces A and C are exchanged and the beauty of the model is that it helps you track all the faces. B and B are also exchanged. So are E and H, but since E and H are a pair, the pair EH maps to itself; that is, E maps to E in the abstraction. Similarly F maps to F:
\[ EAC = \begin{pmatrix}
A \ B \ C \ D \ E \ F \\
C \ D \ A \ B \ E \ F
\end{pmatrix} = (A \ C) (B \ D). \]
EAC is my notation for this rotation. There are 15 of them altogether, considering that there are 30 edges, and each is of order 2; that much is obvious from the geometry, but interestingly each is a product of two transpositions, two other faces being unmoved (face pairs really).
There is a third type of vertex rotation. Draw a line between two opposite vertices and you can rotate the figure by 120° and 240° and have it coincide with itself. Consider a 120° clockwise rotation about vertex 2 in the physical model, the vertex at the juncture of faces A, B, and C. It obviously cycles those three faces and similarly for the other three:
\[ VABC1 = \begin{pmatrix}
A \ B \ C \ D \ E \ F \\
B \ C \ A \ F \ D \ E
\end{pmatrix} = (A \ B \ C) (D \ F \ E). \]
That's the 120° rotation, VABC2 is the 240° rotation around the same axis. These vertex rotations have order three and each is the product of two 3-cycles. There are 20 vertices, therefore 10 vertex pairs, each with two rotations, so there are 20 vertex rotations altogether. That's all of them, so putting it all together:
| Type | Number | Order | Example |
|---|---|---|---|
| F (face) | 24 | 5 | FA1 = (BCDEF) |
| E (edge) | 15 | 2 | EAC = (AC)(BD) |
| V (vertex) | 20 | 3 | VABC1 = (ABC)(DFE) |
| I (identity) | 1 | 1 | I |
| Total | 60 |
So our group has 60 elements and it is non-Abelian since, for example:
\[ {EAC \cdot VABC1} = {FA4 \neq FC4} = {VABC1 \cdot EAC }. \]
The product on the left fixes A, executing the two permutations left to right, while the product on the right takes A to D. There are exactly 60 ways of situating a dodecahedron in space. There are five orientations with face A up, for example, mutually reachable through the FA rotations. There are 12 faces, so the total number of orientations = (# faces) x (#orientations for each face) = 12 x 5 = 60. This implies that a single rotation can take the dodecahedron from any orientation to any other. There are a number of non-Abelian groups of order 60, so the next task is to determine which our group is.
I've written a toolkit to manipulate the rotations. PHP is a good choice because of its ease in handling associative arrays. Array indices can be "A", "B", and so on to represent the permutations naturally. The first task was to build the 60 permutations as arrays and I'm adding two other indices for each one — "T" for the tag, with values like "EAC"; and "P" for the cycle decomposition, with values like "(AC)(BD)". There are functions to calculate products, inverses, conjugates, and so on, and to tell if two permutations are the same. Here's a routine to multiply EAC by VABC1 both ways:
$r = getRotationFromTag("EAC");
$s = getRotationFromTag("VABC1");
print_r($r);
print_r($s);
print_r(product($r, $s));
print_r(product($s, $r));
Array Array
( (
[A] => C [A] => B
[B] => D [B] => C
[C] => A [C] => A
[D] => B [D] => F
[E] => E [E] => D
[F] => F [F] => E
[P] => (AC)(BD) [P] => (ABC)(DFE)
[T] => EAC [T] => VABC1
) )
Array Array
( (
[A] => A [A] => D
[B] => F [B] => A
[C] => B [C] => C
[D] => C [D] => F
[E] => D [E] => B
[F] => E [F] => E
[P] => (BFEDC) [P] => (ADFEB)
[T] => FA4 [T] => FC4
) )
The output confirms that these two rotations don't commute, and indeed that:
\[ {EAC \cdot VABC1} = {FA4 \neq FC4} = {VABC1 \cdot EAC }. \]
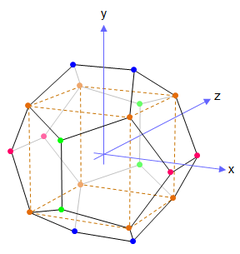
| Vertex coordinates: | |
| The orange vertices lie at (±1, ±1, ±1) and form a cube (dotted lines). | |
| The green vertices lie at (0, ±1/φ, ±φ) and form a rectangle on the y–z plane. | |
| The blue vertices lie at (±1/φ, ±φ, 0) and form a rectangle on the x–y plane. | |
| The pink vertices lie at (±φ, 0, ±1/φ) and form a rectangle on the x–z plane. | |
| The distance between adjacent vertices is 2/φ, and the distance from the origin to any vertex is √3. φ = (1 + √5) / 2 is the golden ratio. |
|
Each edge rotation together with the identity forms a subgroup of order 2. The 20 vertex rotations similarly break into 10 subgroups of order 3. So too for the face rotations; each block of four associated with the same face forms a group of order 5 together with the identity, and there are 6 of them.
The Sylow 2-subgroups have order 4, and since there are no elements of order 4 in \( \mathcal{G} \), they are Klein four-groups. There are 5 of them. To see this, consider the three edge rotations:
\( {EAC = (AC)(BD)} \\ {EEF = (AC)(EF)} \\ {EBD = (BD)(EF)}. \)
It's obvious they all commute because all the transpositions do, being disjoint, and \( (AC)^2 = (BD)^2 = (EF)^2 = I \); also, the product of each pair of rotations equals the third one. The geometry behind it is revealed by the diagram and explanation, stolen shamelessly from Wikipedia (tip of the hat to Another Matt and other astute Wikipedia mathematicians). They point out that a dodecahedron can be situated in 3-space with vertices:
\( (\pm 1, \ \pm 1, \ \pm 1) \\ (0, \ \pm 1/\phi, \ \pm \phi)\\ (\pm 1/\phi, \ \pm \phi, \ 0) \\ (\pm \phi, \ 0, \ \pm 1/\phi), \)
where \( \phi = {{(\sqrt{5} + 1)} / 2} = {1.618 \ldots} \) is the golden ratio. In the diagram, focus on the edge at the very top connecting blue vertices. Assume that edge connects faces A and C. I'll use the notation \( \overline{\mbox{AC}} \) for that edge and the edges come in pairs too, with rotations preserving edge pairs — \( \overline{\mbox{AC}} \)'s matching edge at the very bottom also has blue vertices. Just like faces A and L are denoted jointly by A, so the two blue edges at top and bottom are denoted by \( \overline{\mbox{AC}} \). Two opposite edges form a rectangle in the \( x-y \) plane of height \( 2 \phi \) and width \( 2 \cdot {1 / \phi} \). Its aspect ratio is therefore \( {\phi / (1 / \phi)} = \phi^2 = {\phi + 1} = 2.618 \ldots \). The green vertices connect two pairs of edges making up another rectangle congruent to the first one and perpendicular to it, being in the \( y-z \) plane; they could be \( \overline{\mbox{EF}} \). So too the pink vertices connect two pairs of edges making up a third rectangle congruent to the other two and perpendicular to them, being in the \( x-z \) plane, and they are \( \overline{\mbox{BD}} \).
\( EAC \) turns around each blue edge, exchanges the green ones, and also exchanges the pink ones. So as far as the edge pairs are concerned, \( EAC \) preserves all three of \( \overline{\mbox{AC}} \), \( \overline{\mbox{EF}} \), and \( \overline{\mbox{BD}} \). Faces A and C are obviously exchanged. The green edges connect faces B and G and also D and J — the face pairs denoted by B and D in the abstraction, since face J is opposite B and G is opposite D. \( EAC \) acts to exchange them. The pink edges connect faces E and F and also H and I; the latter is the same as the former, considering that H is opposite E and I is opposite F, and \( EAC \) acts to preserve both E and F.
In a similar vein, \( EEF \) also preserves \( \overline{\mbox{AC}} \), \( \overline{\mbox{EF}} \), and \( \overline{\mbox{BD}} \), exchanging faces A and C and also E and F, leaving B and D unchanged. The upshot is that applying \( EAC \) and then \( EEF \) preserves \( \overline{\mbox{AC}} \), \( \overline{\mbox{EF}} \), and \( \overline{\mbox{BD}} \), exchanging faces B and D and also E and F, leaving A and C unchanged. In other words:
\[ {EAC \cdot EEF} = EBD, \]
evident from the permutation decomposition, but geometrically reasonable too because of those three pairs of opposite edges. The foregoing implies that these self-contained edge rotations form a Klein four-group:
\[ \mathcal{V} = {\{EAC, \ EEF, \ EBD\}}. \]
There are five such configurations in the dodecahedron, and each leads to a Klein four-group in the same way; these subgroups are disjoint other than the identity and they include all the edge rotations (5 groups x 3 rotations per group = 15 rotations). Klein puts it this way, referring to the group named after him as the quadratic group:
Here, however, arises the fact that in the case of the quadratic group the principal axis is equivalent with the two secondary axes. In correspondence with this we obtain only 5 mutually associated quadratic groups. These correspond one by one to the 5 rectangular triads into which we can divide the 15 cross-lines.
Each 3-element subgroup generated by a vertex rotation is embedded in a copy of \( D_3 = S_3 \), so there are 10 copies of \( D_3 \). An example is:
\[ \mathcal{K} = {\{ I, \ VABC1, \ VABC2, \ EDE, \ EDF, \ EEF \}}. \]
To see that this is \( D_3 \), put \( a = VABC1 \) and \( b = EDE \). By direct calculation (or using the toolkit!):
\[ a^3 = b^2 = 1, \hspace{8pt} bab = VABC2 = a^{-1}, \]
relations defining \( D_3 \).
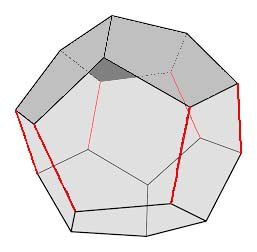
To understand the geometry involved, stand the dodecahedron on the table straight up on vertex LJK, so vertex ABC is at the top — in this image the three gray faces at the top are faces A, B, and C, one of them peeking from behind in dark gray. The three-face cap at the top is opposite one at the bottom and the six red edges connect the two caps. The red edges come in three opposite pairs, namely \( \overline{\mbox{EDE}} \), \( \overline{\mbox{EDF}} \), and \( \overline{\mbox{EEF }}.\) Each one of those edge pairs, thought of as a rotation, turns the docahedron upside down, taking faces A, B, and C into faces L, J, and K in some order. In terms of the face pair abstraction, each edge sends faces A, B, and C into themselves in some order.
Any cyclic permutation of faces A, B, and C followed by one of the edge rotations has the same effect as one of the other three edge rotations; in other words, it simply turns the dodecahedron upside down with face pairs A, B, C mapping to each other in some order. Two edge rotations applied one after the other turn the dodecahedron upside down, then right side up again, the net effect being to permute faces A, B, and C, the faces themselves, not face pairs. In any event, \( \mathcal{K} \) is closed and therefore a subgroup, thought of as a set of rotations.
That's for one pair of vertices and there are 10 in all, so there are 10 subgroups like \( \mathcal{K} \), all isomorphic to \( D_3 \).
Each 5-element subgroup generated by a face rotation is embedded in a copy of \( D_5 \), an example being:
\[ \mathcal{L} = {\{ I, \ FA1, \ FA2, \ FA3, \ FA4, \ ECE, \ EBD, \ EBE, \ ECF, \ EDF \}}. \]
To see that this is \( D_5 \), put \( a = FA1 \) and \( b = ECE \):
\[ a^5 = b^2 = 1, \hspace{8pt} bab = FA4 = a^{-1}, \]
relations defining \( D_5 \).
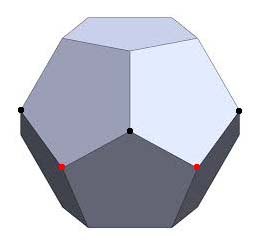
The geometry is similar to that for \( D_3 \). Consider the dodecahedron as sitting flat on a table as suggested here with face A at the top and face L at the bottom. The FA rotations spin the figure around an axis perpendicular to the table, face L never leaving the table. The ten edges along the midsection, each connected by a red and black point, come in pairs — they actually define five edge rotations, the ones in \( \mathcal{L} \). Each of those edge rotations flips the figure, exchanging top and bottom, faces A and L. That is, they all leave A unchanged, thought of as a face pair. The crux of it is that any FA rotation followed by one of those five edge rotations results in another FA rotation, and the same is true if the rotations are done in the other order.
In the same vein, two of those edge rotations one after the other map face A to L and then back to A, so their product is one of the FA rotations. There are six copies of \( \mathcal{L} \) in \( \mathcal{G} \), one for each face pair.
A possible order for subgroups is 12, and indeed there are 5 copies of \( A_4 \) in \( \mathcal{G} \). Any group of order 12 has subgroups of orders 3 and 4, and it develops that each Klein four-group in \( \mathcal{G} \) is associated with one of the copies of \( A_4. \) Short routines in the toolkit produce one such group:
\[ \small{\mathcal{M} = {\{ I, \ EAF, \ EBE, \ ECD, \ \color{blue}{VABC1, \ VABC2}, \ VBFD1, \ VBFD2, \ VFEC1, \ VFEC2, \ VADE1, \ VADE2} \}}. \]
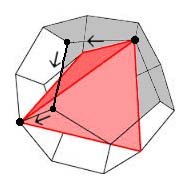
Those four vertices determine a regular tetrahedron. Suppose vertex VABC is the one pictured here at the top right with the big point. It is at the junction of faces A, B, and C, shown in gray; say A is on top, B to the right, and C to the front in the image. Starting from VABC, move along the edge connecting A and C until coming to the next vertex, then take a left turn, coming down the second edge, shown a little thicker. At the next vertex, take a right turn taking you to a third vertex. That third vertex, shown here at the lower left with another big point, is one of the vertices of the tetrahedron connected with VABC. To find the second vertex, set out again from VABC, this time along the edge connecting faces A and B; in the image here that is up and to the right and mostly to the rear in a z sense. Then take a left at the first vertex and a right at the second one; the final point is the third vertex of the tetrahedron. Finally set out from VABC along the edge connecting faces B and C, down and to the right in the image, and proceed in the left-right fashion to determine the fourth point of the tetrahedron.
In finding the second vertex of the tetrahedron, the middle edge traversed is \( \overline{\mbox{CD}} \); it is shown thickened in the picture and its orthogonal partners are \( \overline{\mbox{AF}} \) and \( \overline{\mbox{BE}} \), the three making up one of the Klein four-groups, together with the identity. Any of these edge rotations applied to the vertices of the tetrahedron simply rotates it into itself, that's the geometry of \( \mathcal{M} \) and why it is closed under composition of rotations. The group of rigid motions of a regular tetrahedron is \( A_4 \), so \( \mathcal{M} = A_4 \).
That's one tetrahedron. Do the same for the other vertices defining face A — VACD, VADE, VAEF, and VAFB, making sure to trace out the left-right route in all cases. That will determine another four tetrahedra, and starting with any of the the other fifteen vertices duplicates one of the five tetrahedra already found. Each of those tetrahedra determines a copy of \( A_4 \), just like \( \mathcal{M} \) does, so there are five copies of \( A_4 \) in \( \mathcal{G} \), one for each tetrahedron.
There are another five inscribed tetrahedra, incidentally, those produced by proceeding right-left, instead of left-right. That stands to reason, because each of the five inscribed cubes has two different tetrahedra inscribed in it. The right-left complex of five tetrahedra produces the same groups as the left-right complex though.
There is only one kind of group of order 15, the cyclic one. \( \mathcal{G} \) has no elements of order 15, so it can't have a subgroup of that size. The only remaining possibilities are subgroups of order 20 or 30, and it turns out there are none of those either, so here is the complete list of subgroups of \( \mathcal{G} \):
| Order | #Subgroups | Type | Example (if small) |
|---|---|---|---|
| 1 | 1 | — | |
| 2 | 15 | \( Z_2 \) | \( \{I, \ EAD\} \) |
| 3 | 10 | \( Z_3 \) | \( \{I, \ VABC1, \ VABC2\} \) |
| 4 | 5 | \(V\) | \( \{I, \ EAC, \ EEF, \ EBD\} \) |
| 5 | 6 | \( Z_5 \) | \( \{I, \ FA1, \ FA2, \ FA3, \ FA4\} \) |
| 6 | 10 | \( D_3 \) | \( {\{ I, \ VABC1, \ VABC2, \ EDE, \ EDF, \ EEF \}} \) |
| 10 | 6 | \( D_5 \) | |
| 12 | 5 | \( A_4 \) | |
| 60 | 1 | \( \mathcal{G} \) | |
| Total | 59 |
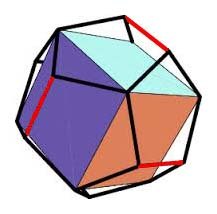
1) Elements of order 2. Conjugacy preserves order and each conjugacy class divides 60, the order of the group, so at first blush the 15 edge rotations might be broken into multiple classes of various sizes. The five Klein four-groups they break into are all conjugate to each other though, being Sylow 2-groups, so conceivably we could have 3 classes of 5 elements each, each class with one element from each four-group. As it happens, all three elements in any of the four-groups are themselves conjugate, so the entire set of 15 edge rotations is one conjugacy class.
To see this, consider that each Klein four-group is an orthogonal set of edge pairs as pictured in red here. The group is associated with one of the 5 inscribed cubes, the one whose faces and edges are themselves orthogonal to the system of edges in the four-group. The rotations preserving the cube are exactly those in the four-group and the 8 vertex rotations with the vertex of rotation the same as a cube vertex (very clear with a model in hand and cube edges drawn on the pentagonal faces). For sake of example, assume the four-group is:
\[ \mathcal{V}' = {\{I, \ EAB, \ EDE, ECF\}}. \]
One of the cube vertices is \( ACD \), and indeed (toolkit!):
\[ {VACD2^{-1} \cdot EAB \cdot VACD2} = EDE, \]
confirming that \( EAB \) and \( EDE \) are conjugate. The geometry of it is that the product on the left maps the cube to itself, but is also an element of order 2, so must be an element of \( \mathcal{V}' \). It follows that the 15 edge rotations form one conjugacy class.
2) Elements of order 3.The 10 copies of \( Z_3 \) are Sylow-3 groups and therefore all conjugate to each other. But the elements of any one those subgroups are conjugate to each other as well, using exactly the same relation as above in the \( D_3 \) section:
\[ {EDE \cdot VABC1 \cdot EDE} = {VABC1^{-1}} = VABC2. \]
Therefore all the elements of order 3 are conjugate and form one conjugacy class.
3) Elements of order 5. There are 24 elements of order 5, the face rotations. They can't all be in one conjugacy class, because \( 24 \not| \;\ 60 \). All the ±72° rotations (the FX1s and FX4s) are conjugate though, as suggested by these equations:
\[ \begin{equation}{{EAC \cdot FC1 \cdot EAC} = FA1,} \tag{1} \end{equation} \]\[ \begin{equation}{{EAC \cdot FC4 \cdot EAC} = FA4,} \tag{2} \end{equation} \]\[ \begin{equation}{{EBD \cdot FA1 \cdot EBD} = FA4.} \tag{3} \end{equation} \]
The first two have a nice symmetry and you can see (1) work with the model by placing the dodecahedron with face A up and A's vertices numbered 1, 2, 3, 4, 5 in clockwise order. Apply EAC, bringing face C to the top. Apply FC1, rotating face C clockwise by 72°. Finally, apply EAC again, which brings face A back to the top. You'll see that the final configuration is identical to the original one, except that face A has been rotated 72° clockwise — the three rotations on the left applied one after the other have the same net effect as FA1. (2) is derived similarly, except that -72° rotations are involved. (3) shows the one of the 72° (FA1) rotations is conjugate to its -72° companion (FA4). Similar formulas obtain for other faces, and it follows that all the ±72° rotations are conjugate.
Squaring (1), (2), and (3) results in the following, after some cancellation:
\[ \begin{equation}{{EAC \cdot FC2 \cdot EAC} = FA2,} \tag{4} \end{equation} \]\[ \begin{equation}{{EAC \cdot FC3 \cdot EAC} = FA3,} \tag{5} \end{equation} \]\[ \begin{equation}{{EBD \cdot FA2 \cdot EBD} = FA3.} \tag{6} \end{equation} \]
Therefore all twelve ±144° rotations (the FX2s and FX3s) are conjugate as well, so the elements of order 5 break into two conjugacy classes, each of size 12.
It's been established that the conjugacy classes of \( \mathcal{G} \) are of sizes 1, 12, 12, 15, and 20. A normal subgroup is a union of those disjoint classes, including the one of size one which contains the identity. But there is no subsetset of these numbers which, added up, divides 60, except all of them, so \( \mathcal{G} \) has no non-trivial normal subgroup and it is simple. The argument is straight from Felix Klein, who uses the word einfach, close to simple in German I believe, but for some reason rendered as primitive in the English translation.
There is only one simple group of order 60 — \( A_5 \), the alternating group on 5 letters, so \( \mathcal{G} \simeq A_5 \). An isomorphism can be produced based on the foregoing. Each of the Klein four-groups consists of three edge rotations together with the identity. Focusing on the edges themselves in each group rather than the rotations, each subset consists of three mutually orthogonal edges :
\[ {E_1 ={\{\overline{\mbox{AB}}}, \ {\overline{\mbox{CF}}}, \ {\overline{\mbox{DE}}}\}}, \\
{E_2 ={\{\overline{\mbox{AC}}}, \ {\overline{\mbox{BD}}}, \ {\overline{\mbox{EF}}}\}}, \\
{E_3 ={\{\overline{\mbox{AD}}}, \ {\overline{\mbox{BF}}}, \ {\overline{\mbox{CE}}}\}}, \\
{E_4 ={\{\overline{\mbox{AE}}}, \ {\overline{\mbox{BC}}}, \ {\overline{\mbox{DF}}}\}}, \\
{E_5 ={\{\overline{\mbox{AF}}}, \ {\overline{\mbox{BE}}}, \ {\overline{\mbox{CD}}}\}}. \]
Like the face pairs, each set of edges moves together when the dodecahedron is rotated. That is, a rotation effects a permutation of the \( E_i \). Call this map \( \Phi \), so \( \Phi(FA1) \), say, is the permutation of the \( E_i \) caused by executing \( FA1 \), and so on:
\[ \Phi(FA1) = \begin{pmatrix}
E_1 \ E_2 \ E_3 \ E_4 \ E_5 \\
E_2 \ E_3 \ E_4 \ E_5 \ E_1
\end{pmatrix} = (1 \ 2 \ 3 \ 4 \ 5), \]
\[ \Phi(VABC1) = \begin{pmatrix}
E_1 \ E_2 \ E_3 \ E_4 \ E_5 \\
E_4 \ E_1 \ E_3 \ E_2 \ E_5
\end{pmatrix} = (1 \ 4 \ 2), \]
\[ \Phi(EAB) = \begin{pmatrix}
E_1 \ E_2 \ E_3 \ E_4 \ E_5 \\
E_1 \ E_3 \ E_2 \ E_5 \ E_4
\end{pmatrix} = (2 \ 3)(4 \ 5), \]
the cycle notation on the right representing \( E_i \) by \( i \).
\( \Phi \) is obviously a homomorphism, considering that applying two rotations one after another results in the same re-arrangement of the edge triples as applying the product rotation directly. Notice in the examples that \( \Phi \) preserves order, as homomorphisms must do, so the image of \( \Phi \) consists of even permutations in \( S_5 \) — 3-cycles, 5-cycles, and products of transpositions. That is, \( \Phi : \mathcal{G} \longrightarrow \mathcal{A} \subseteq A_5 \). On the face of it \( \mathcal{A} \) may be strictly contained in \( A_5 \), but it's not, because the kernel of a homomorphism is a normal subgroup. Therefore \( {\ker(\Phi) = 1,} \ {\text{Im}(\Phi) = A_5,} \) and \( \Phi \) is an isomorphism between \( \mathcal{G} \) and \( A_5 \).
Here it is in Klein's words:
Leaving again the proof that, besides those enumerated, no other sub-groups of the ikosahedral group exist, let us only further observe the isomorphism which arises in the case of the ikosahedral group from the existence of the aforesaid 5 rectangular triads. It can be shown that for every rotation of period 5 these triads are cyclically interchanged in a definite order. For each rotation of period 3, on the other hand, 2 of the triads remain unaltered, and only the other 3 are interchanged in cycle. Finally, it appears that for every rotation of period 2 one of the triads remains unaltered, while the other 4 are interchanged in pairs. In this manner it is shown that the group of the 60 ikosahedral rotations is holohedrically isomorphous [isomorphic] with the group of 60 even permutations of 5 things.
Surprisingly, that \( \mathcal{G} \simeq A_5 \) is non-Abelian and simple is intimately related to the insolvability of the quintic, a connection going back to Abel and Galois. Klein's book is titled Lectures on the Ikosahedron and the Solution of Equations of the Fifth Degree, a further development of this association. This was a perfect topic for him, exemplifying the utility of group theory in uniting geometry, at the same time relating it to the theory of substitutions (permutation groups and polynomial equations) and analysis generally.
Mike Bertrand
February 12, 2015
^ 1. Lectures on the Ikosahedron and the Solution of Equations of the Fifth Degree, by Felix Klein. 1888 (English translation, Ballantyne Press). Originally published in Leipzig in 1884 as Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade.
^ 2. A Comparative Review of Recent Researches in Geometry, aka the Erlangen Program, by Felix Klein, 1872.
^ 3. The Genesis of the Abstract Group Concept, by Hans Wussing (The MIT Press, 1984), ISBN 0-262-23109-3). Originally published in 1969 in the GDR as Die Genesis des Abstrakten Gruppenbegriffes.
^ 4. "On the Symmetry Group of the Dodecahedron", by Lorraine L. Foster (Mathematics Magazine, Vol 63, No 2 — April 1990).