Euclid's Greatest Hits

Like the Bible, Euclid's Elements is revered as a font of ancient wisdom and has indeed served as a kind of bible for those seeking knowledge for 2300 years. The Elements is the foremost scientific text of western civilization and has been studied assiduously since the day it was written around 300 BCE, not only for its mathematical content, but also as a template for how to think clearly. It was one of the very first printed scientific works[1] and became a foundation stone of the revival of mathematics in the Renaissance made possible by printing, vernacular as well as Latin versions falling from the presses like autumn leaves starting in earnest in the sixteenth century.[2] Isaac Newton, for example, studied the Elements carefully and wrote the Principia very much in a Euclidean spirit, augmented by limiting processes.[2a]
Basic familiarity with the Elements has been taken as prerequisite to being considered educated since its advent, the evidence extending from an early scrap at the first cataract[3] to the school background of people now living. The spell is starting to break recently due to an emphasis on discrete mathematics appropriate to the computer age, and even that unfairly discounts the considerable amount of number theory in the Elements.
Resources abound. The first stopping place online is David Joyce's astounding repository of the entire text of the Elements, with each proposition and its proof on a single page followed by commentary. Click through the table of contents to the books and individual propositions. As of this date (May 2022), Googling Euclid Joyce I 47 takes you to Euclid I.47 and so on for the others. The original Java applets are now passe unfortunately with the deprecation of that technology.
The canonical English translation is that of Sir Thomas Heath of 1908, based on Heiberg's authoritative Greek and Latin edition of 1883-1888.[3a] Heath's Euclid is available online and in cheap reprints (I recommend the three-volume Dover edition of 1956, which contains all of Heath's invaluable commentary).[4] My statements of the propositions below are from Professor Joyce, who follows Heath closely but not exactly. An auxiliary book I've found particularly helpful is Benno Artmann's Euclid: The Creation of Mathematics, which goes through the Elements in detail, highlighting important propositions, giving Euclid's proofs, and adding commentary and modern notation on occasion.[5]
The purpose of this article is to discuss twelve key theorems in the Elements and to prove them as Euclid did, trying to put their importance in the context of later developments. The Elements contains thirteen books (chapters) — see the Wikipedia article for a good breakdown of the content of each. In what follows, the books are designated by Roman numerals and the propositions by numbers, so III.31 refers to Book III, Proposition 31. The square on segment \(AB\) is denoted \(\square AB,\) and the triangle with vertices \(E, F, G\) is \( ▵EFG.\) The rectangle with opposite corners \(B\) and \(D\) is denoted by \(\Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!BD,\) while the rectangle on segments \(AB, CD\) is \(\Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!(AB, CD).\) Line \(AB\) is parallel to line \(CD\) is denoted by \(AB ∥ CD.\)[6] Euclid identifies a planar figure with its area in writing about it: he would say that the square with vertices \(A, B, C, D\) is twice \(▵ABC,\) for example.
I.32. In any triangle, if one of the sides is produced, then the exterior angle equals the sum of the two interior and opposite angles, and the sum of the three interior angles of the triangle equals two right angles.

Proof. Let the triangle be \(ABC\) and extend segment \(BC\) to \(D.\) Draw segment \(CE\) with \(E\) on the same side of line \(BCD\) as \(A\) and \(CE\) parallel to \(BA.\) Then \(∠BAC = ∠ACE\) because they are alternate interior angles when parallel lines \(BA\) and \(CE\) are cut by transversal \(AC\) (I.29). \(∠ECD = ∠ABC\) because they are the exterior and opposite interior angles when parallel lines \(BA\) and \(CE\) are cut by the transversal \(BD\) (I.29). Denoting the angles of the triangle by \(∠A, ∠B, ∠C,\) this leads to:
\[∠A + ∠B + ∠C = ∠ACE + ∠ECD + ∠C,\]
but the three angles on the right array along a straight line, so their sum is two right angles or \(180^\circ.\) QED.
This is one of the great truisms of mathematics, on a plane with \(1 + 1 = 2,\) but it must be proven and the proof is not obvious until put in the context of parallel lines as discussed earlier in Book I. Euclid's tactic of drawing auxiliary lines or figures is fully on display here.
I.47. In right-angled triangles the square on the side opposite the right angle equals the sum of the squares on the sides containing the right angle.

Proof. Let the triangle be \(ABC,\) with right angle at \(A.\) Construct the squares outward on each leg and draw a line from \(A \) perpendicular to \(BC\) and down through the triangle and the square opposite, labeling points as shown in the diagram. The first step is to show that the colored triangles are congruent. The obtuse angle in yellow triangle \(▵ABD\) is a right angle plus the triangle's angle at \(B.\) The obtuse angle in the gray triangle is a another right angle plus the triangle's angle at \(B.\) Therefore those two angles are equal and the two triangles are congruent by side-angle-side (SAS, which is I.4).
Next is to note that yellow triangle \(▵ABD\) and rectangle \(BL\) are on the same base \(BD\) and are between parallel lines \(BD\) and \(AL,\) so \(BL\) is twice \(▵ABD\) (I.41). A similar effect applies to the gray rectangle, where now the base is \(FB\) and the parallel lines are \(FB\) and \(GAC\) (that \(GAC\) is a straight line is due to the right angle in the triangle at \(A!\)). This shows that \(\square AB\) is twice \(▵BFC.\) It follows that \(\Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!BL = \square AB.\) A similar argument shows that \(\Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!CL = \square AC.\) Since the two rectangles make up square \(BC,\) it follows that \(\square BC = \Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!BL + \Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!CL = \square AB + \square AC.\) QED.
The Pythagorean Theorem is the most venerable, important, and well known theorem in mathematics. Like virtually all of the Elements, its lineage predates Euclid and in this case by a good deal. Pythagoras himself lived ~570 — 490 BCE, some two hundred years before Euclid. But there are strong indications that the old Babylonians knew of the Pythagorean Theorem as early as 1800 BCE, using it to calculate \(\sqrt{2} = 1.41421 \, 2963\) (the correct value is \(1.41421 \, 3562\)). Of course Euclid and presumably the Pythagoreans before him were the first known to prove it and therein lies the epochal significance of the Elements.
First is this lemma:
II.6. If a straight line is bisected and a straight line is added to it in a straight line, then the rectangle contained by the whole with the added straight line and the added straight line together with the square on the half equals the square on the straight line made up of the half and the added straight line.

Proof. Let \(AB\) be the original straight line, bisected at \(C\) and with \(BD\) the straight line added to it. Construct the square on \(BD\) with vertices \(B, D, M, H.\) Construct the rectangle on \(CB\) and \(BH\) with vertices \(C, B, H, L.\) Construct the rectangle on \(AC\) and \(CL\) with vertices \(A,C, L, K.\) Next Construct the square on \(LH\) on the side opposite \(CB\) with vertices \(L, H, G, E.\) Finally construct the rectangle on \(MH\) and \(HG\) with vertices \(M, H, G, F.\) Note that \( AC = CB = LH = HG\) and \( AK = DM = HM,\) consequently the two gray rectangles are equal: \(\Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!AL\) = \(\Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!HF.\) Because \(LH = CB, \square CD\) equals \(\square LH\) plus the L-shaped figure outlined by dashed lines, known as the gnomon on \(CB, BD.\) But because the two gray rectangles are equal, the gnomon equals \(\Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!AM = \Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!(AD, BD).\) It follows that \(\Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!(AD, BD) + \square CB = \square CD.\) QED.
Euclid introduces the gnomon in I.43 in connection with parallelograms. He proves there that \(\Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!CH = \Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!HF\) in the diagram above. Euclid had no truck with algebra, but those who do might put it this way — if \(a = CB\) and \(b = BD:\)
\begin{align}
\square CD &= \square CB \; + \Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!CH \; + \Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!HF + \square BD\\
&= \square CB + 2 \; \cdot \Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!CH + \square BD\\
\therefore (a + b)^2 &= a^2 + 2ab + b^2.
\end{align}
Next is the theorem on the Golden Section:
II.11. To cut a given straight line so that the rectangle contained by the whole and one of the segments equals the square on the remaining segment.

Proof. Let \(AB\) be the original straight line. We want a point \(H\) in its interior such that the square on \(AH\) equals the rectangle on segments \(AB\) and \(HB.\) First construct the square on \(AB\) and below \(AB\) as shown. Bisect \(AC\) at point \(E.\) Connect \(E\) to \(B\) by a straight line and draw circular arc \(BF\) centered at \(E\) and meeting the extended line \(CEA\) above \(AB\) at \(F.\) Construct square \(AFGH\) above line \(AB,\) extending line \(GH\) down to meet \(CD\) at \(K\). The objective is to show that the colored square and rectangle are equal. Applying the Pythagorean Theorem to \(▵AEB\) and noting that \(FE = BE\) by construction:
\begin{align}
\square BE &= \square AE + \square AB\\
\therefore \square FE &= \square AE + \square AB.\tag{1}
\end{align}
II.6 applies to the vertical line \(CEAF,\) giving another expression for \(\square FE:\)
\[\square FE = \; \Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!(CF,FA) + \square AE.\tag{2}\]
Equating the right sides of (1) and (2) gives:
\begin{align}
\square AE + \square AB &= \; \Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!(CF,FA) + \square AE\\
\square AB &= \; \Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!(CF,FA)\\
\square AB &= \; \Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!(CF,FG).\tag{3}
\end{align}
Removing \(\Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!AK\) from both figures in (3) results in \(\square AH = \; \Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!HD = \; \Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!(HB,AB)\). QED.
The ratio \(\varphi=AH/HB\) is called the golden section or the golden ratio and has long been a subject of fascination. For the Pythagoreans, it was intimately associated with the pentagram and the regular pentagon, considering that it is the ratio of the diagonal of a regular pentagon to its side. Euclid uses this proposition to construct a \(72^\circ-72^\circ-36^\circ\) triangle in IV.10, a short step from the regular pentagon (IV.11). Putting \(x = AH, HB = 1,\) the proposition says that:
\begin{align}
&x^2 = 1 \cdot (x+1) = x+1\\
\therefore \; &x^2 - x - 1 = 0,
\end{align}
solving which results in:
\[ \varphi = x = {{\sqrt{5}+1} \over {2}} \sim 1.618033989.\]
The golden section is intimately related to the Fibonacci numbers as well. The term "golden section" sectio aurea was evidently coined by Leonardo da Vinci, who illustrated Luca Pacioli's book Divina proportione of 1509, also named after the golden section. Pacioli and others have noted the ubiquity of the golden rectangle (the rectangle with aspect ratio \(\varphi\)) in art, architecture, and nature, deeming it it the most aesthetically pleasing of all rectangles. Wikipedia has a nice write-up of the history.

The Law of Cosines asserts that:
\[a^2 = b^2 + c^2 -2bc \cos{\alpha},\tag{4}\]
where \(a, b, c\) are the sides of a triangle and \(\alpha\) is the angle between \(b\) and \(c.\) It is a generalization of the Pythagorean Theorem. Consider the obtuse angle \(\alpha\) in this diagram. Since \(a = BC,\) the side opposite \(\alpha,\) is longer than if \(\alpha\) were a right angle on sides \(c = AB\) and \(b = AC,\) the square on \(a\) exceeds the sum of the squares on \(b\) and \(c\) and the Law of Cosines says by how much. Since the cosine is negative for obtuse angles, the negative sign in (4) actually increases the value of the right side, as expected. For acute \(\alpha,\) the cosine is positive, so the cosine decreases the value on the right, making the square on \(a\) less than the sum of the squares on \(b\) and \(c.\) Of course, Euclid had no recourse to trigonometry as we know it, but his version is perfectly sound. Below is his proof for obtuse triangles (II.13 is the similar version for acute triangles).
II.12. In obtuse-angled triangles the square on the side opposite the obtuse angle is greater than the sum of the squares on the sides containing the obtuse angle by twice the rectangle contained by one of the sides about the obtuse angle, namely that on which the perpendicular falls, and the straight line cut off outside by the perpendicular towards the obtuse angle.
Proof. Let the triangle be \(ABC\) with obtuse angle \(\alpha\) at \(A.\) Extend \(AC\) on the side of point \(B\) and drop a perpendicular down from \(B\) to that line, meeting it at \(D.\) By the Pythagorean Theorem applied respectively to triangles \(▵BDC\) and \(▵BDA:\)
\begin{align}
\square BC &= \square BD + \square DC\tag{5}\\
\square AB &= \square BD + \square DA\tag{6}\\
\end{align}

in Euclid II.4
In II.4, Euclid proved a geometric version of the binomial theorem as pictured above. In his geometric language:
If a straight line is cut at random, then the square on the whole equals the sum of the squares on the segments plus twice the rectangle contained by the segments.
Applying II.4 to segment \(DC\) cut at \(A:\)
\[\square DC = \square DA + \square AC + 2 \; \cdot \Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!(DA,AC).\tag{7}\]
Combining (5) and (7):
\begin{align}
\square BC &= \square BD + (\square DA + \square AC + 2 \; \cdot \Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!(DA,AC))\\
\square BC &= (\square BD + \square DA) + \square AC + 2 \; \cdot \Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!(DA,AC)\tag{8}\\
\end{align}
Combining (6) and (8) gives the final result:
\[\square BC = \square AB + \square AC + 2 \; \cdot \Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!(DA,AC) \textbf{ QED.}\]
To see that this is equivalent to the Law of Cosines, put \(a = BC, b = AC, c = AB\) and note that \(\cos \alpha = -DA / AB = -DA /c.\) Therefore:
\begin{align}
a^2 &= c^2 + b^2 + 2 \cdot DA \cdot b\\
&= c^2 + b^2 + 2 \cdot (-c \cos{\alpha}) \cdot b.\\
&= c^2 + b^2 - 2bc \cos{\alpha}.\\
\end{align}
Thales (~625-545 BCE) is the first mathematician known by name in the west, that is, the first one to think that mathematical statements need to be proven from more elementary concepts and then proceed to provide proofs. He was reputed to be a great sage and philosopher and is mentioned in the ancient sources, including Aristotle. Thales' Theorem is in Book III:

III.31. In a circle the angle in the semicircle is right ...
Proof. The proposition continues to characterize angles in chords, but that the diameter subtends right angles is Thales' Theorem. Let segment \(BEC\) be the diameter of a circle with center \(E\), and let \(A\) be another point on the circle. Yellow triangle \(▵ABE\) is isosceles on base \(AB\) because the other two legs are radii of the circle. Therefore the indicated angles are equal (call them \(\beta\)). The same is true for the gray triangle \(▵ACE\) with two equal angles \(\gamma\) at the base. But \(∠FAC = \beta + \gamma\) because \(∠FAC\) is the external angle of \(\beta\) and \(\gamma\) in \(▵ABC.\) Since \(∠FAC \) and angle \(\beta + \gamma\) make a straight line, it follows that \(∠FAC\) and \(\beta + \gamma\) are right angles. QED.
Thales' Theorem is a staple of plane geometry and, according to David Joyce, is cited repeatedly from this point forward in the Elements.
Book II features a form of geometric algebra exemplified by II.4, proving in a geometric way what we express algebraically as \((a+b)^2 = a^2 + 2ab + b^2,\) and there are actually three squares and two equal rectangles in play. So it is anachronistic to say that Euclid solved quadratic equations anything like we do. All the same, he provides solutions to quadratic problems we would call quadratic equations, but for him all objects are geometric — line segments, squares, rectangles, and so on.[7] The following construction shows how II.6, cited as a lemma connected to the Golden Section above, leads to a solution of:
\[x^2 + ax = b^2,\tag{9}\]

where \(a\) and \(b\) are line segments (so \(b^2\) is a square). Proceed as in II.6, putting \(a = AB,\) where \(AB\) is a line segment connecting points \(A\) and \(B.\) Cut \(AB\) in half at point \(C.\) Erect a line perpendicular to \(ACB\) at \(B\) of length \(b\) with top point \(Q.\) Draw a circular arc centered at \(C\) going through \(Q,\) meeting \(AB\) extended at \(D.\) Then \(x = DB\) is a solution of (9). To show this, start with:
\begin{align}
AD \cdot DB + CB^2 &= CD^2\\
&= CB^2 + BQ^2,
\end{align}
the first line restating II.6 and the second line applying the Pythagorean Theorem to \(▵BCQ\) and noting that \(CD = CQ\) by construction. It follows that:
\begin{align}
AD \cdot DB &= BQ^2\\
\therefore (a + x)x &= b^2\\
x^2 + ax &= b^2.
\end{align}
Lest it be thought that this approach extrapolates Euclid, VI.29 engages in exactly this construction, but in greatly generalized form, drawing a parallelogram on \(AB\) and augmenting it with another parallelogram \(BM\) similar to a given one and such that the entire parallelogram \(AM\) is equal to a given rectilinear figure. The preceding proposition VI.28 is similar, except that a parallelogram is taken away, leading to a solution of \(ax - x^2 = b^2\) when \(a \geq 2b.\)
Complex numbers weren't invented for another 2000 years, so there is no question of solving a quadratic equation in general. Even negative numbers were under suspicion in European mathematics as late the sixteenth century, so the foregoing only applies to find a positive real root.
This perfectly mirrors the algebraic method of "completing the square" known and beloved(!) by legions of high school scholars. Follow the method to see this:
\begin{alignat}{1}
&(i) \quad &x^2 + ax = b^2\\
&(ii) \quad &x^2 + ax + \left({a \over 2}\right)^2 = \color{red}{b^2+ \left({a \over 2}\right)^2}\\
&(iii) \quad &\left(x + {a \over 2}\right)^2 = b^2 + \left({a \over 2}\right)^2\\
&(iv) \quad &\color{blue}{x + {a \over 2}} =\sqrt{\; b^2 + \left({a \over 2}\right)^2}\\
&(v) \quad &x = \sqrt{\; b^2 + \left({a \over 2}\right)^2} - {a \over 2}.\\
\end{alignat}
Line (ii) here completes the square by adding \((a/2)^2\) to each side, where \(a/2 = CB.\) The right side of (ii) is then the sum of two squares on the legs of right triangle \(▵CBQ\), namely, \(b = BQ\) and \(a/2 = CB.\) So the right side of (ii) and (iii) is the hypotenuse of that triangle, \(CQ = CD.\) Finally, \(x = BD = CD - CB,\) which is (v).
Books VII-IX take up number theory in a quasi-geometric setting. Book VII has twenty-two definitions, including for prime and composite numbers and numbers that are relatively prime. A product of two whole numbers is defined as a plane number, suggesting a rectangular array of dots. Similarly a solid number is a product of three whole numbers, as if a three-dimensional array of dots is being considered. Numbers are envisioned as line segments and the phrase "\(CD\) measures \(AB\)" means \(CD\) divides \(AB.\) A common measure of two numbers is a number dividing (measuring) them both and their greatest common measure is their greatest common divisor. VII.2 is the Euclidean Algorithm, one of the oldest and most important in mathematics:[8]
VII.2. To find the greatest common measure of two given numbers not relatively prime.

Proof. Let \(AB\) and \(CD\) be the two whole numbers and assume, without loss of generality, that \(CD\) is the smaller one. If \(CD\) measures \(AB,\) then \(CD\) itself is the greatest common measure of \(AB\) and \(CD\) (that is, if \(CD\) divides \(AB,\) then \(CD\) is the greatest common divisor of \(AB\) and \(CD\)). Otherwise \(CD\) does not measure \(AB,\) so repeatedly subtracting \(CD\) from \(AB\) as many times as possible leaves remainder \(AE\) less than \(CD.\) So \(CD\) measures \(BE\) and \(AE\) is less than \(CD.\)
Similarly subtract \(AE\) from \(CD\) repeatedly as many times as possible. If there is no remainder, then \(AE\) is a common measure of \(AB\) and \(CD.\) Furthermore, any common measure of \(AB\) and \(CD\) also measures \(AE,\) so \(AE\) is the greatest common measure.
If there is a remainder when \(AE\) is subtracted repeatedly from \(CD,\) let \(CF\) be the remainder and suppose \(\mathbf{CF}\) measures \(\mathbf{AE}.\) Then \(CF\) measures \(DF\) also and therefore \(CF\) measures \(CD.\) \(CF\) also measures \(AB\) and so \(CF\) is a common measure of \(AB\) and \(CD.\)
The final step is to prove that \(CF\) is the greatest common measure of \(AB\) and \(CD.\) To this end, suppose that \(G\) is some common measure of \(AB\) and \(CD.\) Then \(G\) measures \(BE\) (which \(CD\) measures) and so \(G\) measures \(AE.\) But then \(G\) also measures \(DF\) since \(AE\) measures \(DF.\) \(G\) also measures \(CF\) since \(G\) measures \(DF\) and \(CD.\) It follows that \(G\) cannot be larger than \(CF.\) That is, any common measure of \(AB\) and \(CD\) cannot be larger than \(CF\) and so \(CF\) is the greatest common measure of \(AB\) and \(CD.\) QED
The supposition that \(CF\) measures \(AE,\) bolded in the proof, is in general unwarranted, and the contrary assumption would lead to a third line \(JK\) strictly less than \(CD.\) The proof can be saved by adding something like "and so on, in a process that must terminate because the lines become strictly smaller at each step and cannot have length less than one." With that amendment, the proof is perfectly correct, if somewhat painful without modern notation (it takes a page and a half in Heath). The process is identical to that used today, except multiplication is used for the amount subtracted rather than repeated subtraction. Euclid assumes the division algorithm for positive integers:
For positive inegers \(a, b\) with \(b \leq a,\) there are unique integers \(q\) and \(r\) such that \(a = bq + r,\) where \(0 \leqslant r < b.\)
\(a = AB\) and \(b = CD\) here. Consider this example, mirroring Euclid's two-step proof and the diagram in particular, where \(a = AE = 8\) and \(b = CD = 3:\)
\begin{align}
8 &= 2 \cdot 3 + 2\\
3 &= 2 \cdot 1 + 1\\
2 &= 2 \cdot 1
\end{align}
So \(CF = 1\) is the greatest common measure of \(8\) and \(3\). Euclid separated out relatively prime pairs like this because he viewed \(1\) as a very different kind of number if a number at all. But he needn't have — the process is the same whether the values are relatively prime or not (VII.1 concerns relatively prime pairs).
Integral domains with a division algorithm are called Euclidean Domains — they have a Euclidean Algorithm and greatest common divisor and share many of the properties of the integers. If \(F\) is a field, for example, then \(F[x],\) the ring of polynomials of a single variable over \(F\), is a Euclidean domain.
VII.30. If two numbers, multiplied by one another make some number, and any prime number measures the product, then it also measures one of the original numbers.
This is Euclid's Lemma — in modern notation: if \(p \; | \; ab\) for integers \(p, a, b,\) where \(p\) is prime, then \(p \; | \;a\) or \(p \; | \;b.\) It is instrumental in proving the Fundamental Theorem of Arithmetic, that every positive integer greater than one can be uniquely represented as a product of primes, apart from order. A simple inductive argument establishes existence, but Euclid's Lemma is needed for uniqueness. Euclid's proof depends on seemingly innocuous but sophisticated facts about proportions and is problematic.[9] Modern proofs typically depend on a consequence of the Euclidean Algorithm, namely, that if \(a\) and \(b\) are relatively prime integers, then there are integers \(x\) and \(y\) (not necessarily positive!) such that:
\[ax+by=1.\tag{10}\]
(10) is called Bézout's identity. Consider the example of the Euclidean Algorithm applied to \(41\) and \(9\) to see how \(1\) can be gotten as a linear combination of the two:
\begin{align}
41 &= 4 \cdot 9 + 5\\
9 &= 1 \cdot 5 + 4\\
5 &= 1 \cdot 4 + 1.
\end{align}
Rephrasing this from the bottom up:
\begin{align}
1 &= 5 - 1 \cdot 4\\
4 &= 9 - 1 \cdot 5\\
5 &= 41 - 4 \cdot 9.
\end{align}
Plugging the value for \(4\) from the second equation into the first equation results in an expression for \(1\) in terms of \(5\) and \(9\) and then plugging in the value for \(5\) from the third equation into that one results in an expression for \(1\) in terms of \(9\) and \(41:\)
\begin{align}
1 &= 5 - 1 \cdot4\\
&= 5 - 1 \cdot (9 - 1 \cdot 5)\\
&= 2 \cdot 5 - 1 \cdot 9\\
&= 2 \cdot (41 - 4 \cdot 9) - 1 \cdot 9\\
&= 2 \cdot 41 - 9 \cdot 9.
\end{align}
Euclid didn't have negative numbers, so this would have been unintelligible to him. Pengelley and Richman explain how his argument can be patched up in strictly Euclidean terms.[10] Proceed as follows to prove that Bézout implies Euclid's Lemma:
Euclid's Lemma (modern version). If \(p \; | \; ab\) for integers \(p, a, b,\) where \(p\) is prime, then \(p \; | \;a\) or \(p \; | \;b.\)
Proof. Assume \(p \; | \; ab\) but \(p \not | \;a.\) Since \(p \; | \; ab,\) there is an integer \(n\) such that \(pn = ab.\) By Bézout's identity, there are integers \(x\) and \(y\) such that \(px + ay = 1.\) Multiply by \(b\) to get:
\[ pxb + ayb = b.\]
\(p\) obviously divides \(pxb\) and \(p\) also divides \(ayb\) because it divides \(ab.\) It follows that \(p \; | \;b.\) QED.
Primality has been vastly extended in modern algebra with the notion of a prime ideal in a commutative ring, namely, an ideal \(P\) in which \(ab \in P \Rightarrow a \in P\) or \(b \in P.\) Prime ideals in Noetherian rings play a key role analogous to prime numbers in the integers.
This may be the very first proof in THE BOOK, Paul Erdős's whimsical list kept by the Lord of the most beautiful proofs in mathematics.[11]
IX.20:. Prime numbers are more than any assigned multitude of prime numbers.
Proof. Let \(A, B, C\) be given prime numbers. The goal is to prove there is at least one more. Let \(DE\) be the least number measured by \(A, B, C,\) that is, their least common multiple. Since the three original numbers are prime, their least common multiple is their product, not that Euclid mentions or needs this fact. Add the unit length \(DF\) to \(DE\) so that \(EF = DE + 1.\) If \(EF\) is prime, then a fourth prime has been produced and the theorem is proven. Suppose then that \(EF\) is not prime, and let it be measured by some prime number \(G\) (that is, prime number \(G\) divides it) — VII.31 assures such a prime. But then \(G\) is different from any of \(A,B,C.\) For assume otherwise, that \(G\) is one of \(A,B,C.\) Then \(G\) measures both \(EF\) and \(DE\) and therefore their difference \(1,\) which is absurd. Therefore \(G\) cannot be any of \(A,B,C\) and again a fourth prime has been produced. QED.
This proof is a canonical example of proof by contradiction or reductio ad absurdum: assuming the opposite of the theorem to be proven and deriving a contradiction, thereby concluding that the opposite of the original assumption (that is, the theorem) is true. G. H. Hardy gave this exact proof as exemplary, citing it as simple both in idea and in execution, but of the highest class all the same and "as fresh and significant as when it was discovered — two thousand years have not written a wrinkle on [it]":
The proof is by reductio ad absurdum, and reductio ad absurdum, which Euclid loved so much, is one of a mathematician's finest weapons. It is a far finer gambit than any chess gambit: a chess player may offer the sacrifice of a pawn or even a piece, but a mathematician offers the game.[12]
Towards the end, Euclid's proof says "which is absurd", the exact words in Heath's English translation at that point (quod absurdum est in Heiberg's Latin; ἄτοπον, "out of place", in his Greek). Like with the Euclidean Algorithm, Euclid proves a special case and lets it stand for the general proof. Current fashion requires a generalized approach: assume \(p_1, p_2, \ldots, p_n\) constitutes the complete list of primes, where \(n\) is a positive integer, and so on. Apart from the geometric trappings, Euclid's proof is at least as clear as the modern approach and is easily subject to generalization by anyone who understands it. Euclid's prescient attention to prime numbers makes him a pioneer of number theory as well as geometry. This theorem and its proof have stood the test of time and appear in virtually every basic textbook of number theory to this day.
The ancient Greeks spoke of incommensurable line segments or magnitudes rather than irrational numbers, but it amounts to the same thing. Here is Euclid's definition at the start of Book X:
X: Definition 1. Those magnitudes are said to be commensurable which are measured by the same measure, and those incommensurable which cannot have any common measure.

The use of "measure" here is the same as with the Euclidean Algorithm, where a shorter line measures a longer one if the shorter line can be repeatedly laid end-to-end along the longer one a certain number of times, exactly exhausting it. In the diagram, segment \(CD\) measures segment \(AB\) because \(CD\) can be laid against \(AB\) exactly twice. \(EF\) measures both \(AB\) and \(CD,\) so \(AB\) and \(CD\) are commensurable. It is key that the number of repeated layings-on is a positive natural number. Numerically, one number measures another if the the first divides the second. Commensurability and the modern notion of a rational number are virtually equivalent:
Theorem. \(a\) and \(b\) are commensurable if and only if \(a / b\) is rational.
Proof. Suppose \(a\) and \(b\) are commensurable, so there are values \(j\) and \(k\) and a positive natural number \(m\) such that \(a = jm, b = km.\) Therefore:\[{a \over b} = {jm \over km} = {j \over k}.\] Conversely, suppose \(a / b\) is rational. Then \( a = a \cdot 1\) and \(b = b \cdot 1,\) so \(a\) and \(b\) are commensurable. QED.
Note that the the notion of commensurability is relative, so \(\sqrt{2}\) and \(2\sqrt{2}\) are commensurable; or, as Euclid might have put it, the diagonals on a square of side one unit and a square of side two units are commensurable.
Tradition, probably reliably, ascribes the discovery of incommensurables to the Pythagoreans in the fifth century BC.[13] The discovery was momentous and apparently recognized as such at the time, an early scholiast of Book X commenting that "the first of the Pythagoreans who made public the investigation of these matters perished in a shipwreck", commenting that his source:
perhaps spoke allegorically, hinting that everything irrational and formless is properly concealed, and, if any soul should rashly invade this region of life and lay it open, it would be carried away into the sea of becoming and be overwhelmed by its unresting currents.[14]
The Euclidean Algorithm for line segments assures the existence of incommensurable magnitudes:
X.2. If, when the less of two unequal magnitudes is continually subtracted in turn from the greater that which is left never measures the one before it, then the two magnitudes are incommensurable.
Proof. Suppose \(AB\) and \(CD\) are two unequal line sgments with \(AB < CD\) and execute the Euclidean Algorithm on them as described above for positive integers.[15] By hypothesis, the process never ends. Let \(E\) be a given small segment presumed to measure both \(AB\) and \(CD\). Eventually the process results in a segment shorter than \(E,\) which then \(E\) cannot possibly measure. This contradiction proves that \(AB\) and \(CD\) cannot have a common measure, that is, they are incommensurable. QED.
That the process results in increasingly small segments is not a priori clear, but it is true and justified by X.1, vitally important itself (Euclid's "continuity axiom" according to Otto Toeplitz).[15a]
X.1. Two unequal magnitudes being set out, if from the greater there is subtracted a magnitude greater than its half, and from that which is left a magnitude greater than its half, and if this process is repeated continually, then there will be left some magnitude less than the lesser magnitude set out.
Each step in the Euclidean Algorithm results in a remainder less than half the original number being subtracted from (or divided into). To see this, consider each step in the algorithm:
\[a = bq + r, \text{ where } a, b, q \geq 1, \; 0 \leq r < b.\]
It follows that:
\begin{align}
a - bq & < b\\
a & < bq + b\\
a & < bq + bq = 2bq\\
\therefore bq & > a/2\\
r & < a/2,
\end{align}
the last step because \(a = bq + r\) implies that if one of the summands on the right is greater than \(a/2,\) then the other one must be less than \(a/2.\) The placement of X.1 suggests that Euclid meant it to be used in this way (X.1 is not used otherwise until Book XII) — perhaps a scribe overlooked the reference at a key point of transmission.[16]

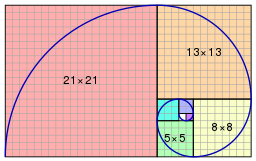
Applying X.II to the diagonal and side of a square results in an infinite regress as spoken of in the proposition, proving that the diagonal and side are commensurable, that is, \(\sqrt{2}\) is irrational. For consider this diagram with an infinite series of smaller and smaller squares spiralling counter-clockwise up and to the right. Starting with the big square \(\square AB,\) draw its diagonal \(AC\) and the circular arc \(DB\) centered at \(A,\) the two meeting at point \(E.\) Draw segment \(EF\) perpendicular to \(AEC,\) meeting \(BC\) at \(F.\) Note that both \(EF\) and \(BF\) are tangent to the circular arc, so \(EF = BF.\) Build out the next square \(CEFG\) and repeat the process ad infinitum as shown — the next one in sequence is the little gray square at the upper right. Apply the Euclidean Algorithm to the diagonal and side of \(\square AB,\) the big square:
\begin{align}
AC &= 1 \cdot BC + EC\\
BC &= 2 \cdot EC + HC\tag{11}\\
EC &= 2 \cdot HC + CK.\tag{12}\\
& \vdots
\end{align}
(11) holds because:
\begin{align}
BC &= BF + FH + HC\\
&= EC + EC + HC\\
&= 2 \cdot EC + HC,
\end{align}
and (12) replicates (11) on a smaller scale. There are four squares of diminishing size in this diagram — large, middle, small, and tiny squares. (11) and (12) can be recast as follows and similarly for the rest of them:
side of medium square = \(2 \, \times\) side of small square + side of tiny square
Each square is \(\sqrt{2}-1=0.414\) as big as the preceding one:
\begin{align}
EC &= AC - AE\\
&=\sqrt{2} AE - AE\\
&=(\sqrt{2}-1) AE\\
&=(\sqrt{2}-1) BC.\\
\end{align}
That the Euclidean Algorithm applied to the diagonal and side of a square goes on forever proves, according to X.2, that they are incommensurable. Expressing this application of the Euclidean Algorithm in modern notation results in:
\begin{align}
\sqrt{2} &= 1 \cdot 1 + (\sqrt{2}-1)\\
1 &= 2 \cdot (\sqrt{2}-1) + (3 - 2\sqrt{2})\\
\sqrt{2}-1 &= 2 \cdot (3 - 2\sqrt{2}) + (5\sqrt{2} - 7)\\
3 - 2\sqrt{2} &= 2 \cdot (5\sqrt{2} - 7) + (17 - 12\sqrt{2})\\
5\sqrt{2} - 7 &= 2 \cdot (17 - 12\sqrt{2}) + (29\sqrt{2} - 41).\\
\end{align}
Those are the sides of the squares along the left, starting with the second equation. The ratios of these integers approach \(\sqrt{2}\) more and more closely with each iteration, with \(41/29 = 1.4138\) \((\sqrt{2} = 1.4142).\)
Archimedes famously proved that \(3 {10 \over 71} < \pi < 3 {1 \over 7}\) by inscribing and circumscribing regular polygons in and around a circle. But it was Euclid who first proved that \(\pi\) exists, considering \(\pi\) to be four times the ratio of the area of a circle to the square of its diameter:
\begin{align}
A &= \pi r^2\\
&= \pi \left({d \over 2}^2\right)\\
&= {\pi \over 4} \cdot d^2\\
\therefore {A \over d^2} &= {\pi \over 4},\tag{13}
\end{align}
where \( A, r, d\) are the area, radius, and diameter of a given circle. This is XII.2, that the ratio on the left side of (13) is the same for any circle:
XII.2. Circles are to one another as the squares on their diameters.

Proof. Start with a given circle \(\Omega\) and inscribe a square in it with side \(AB\) as a chord of the circle. Bisect \(AB\) at \(C\) and draw \(CE\) perpendicular to \(AB\) at \(C,\) meeting the circle at \(E,\) which then bisects arc \(AB.\) \(AE\) and \(EB\) are sides of a regular inscribed octagon, and the octagon can be completed in the same way. Let \(\Sigma_2\) be the sum of the four circular segments bounded by the chords forming the square — the colored segment, light and dark gray both, is one of the four segments making up \(\Sigma_2.\) Likewise let \(\Sigma_3\) be the sum of the eight circular segments bounded by the chords forming the regular octagon, of which the dark gray segments are two. The first step is to prove that \(\Sigma_3 < {{1}\over{2}} \Sigma_2.\) To this end, build out rectangle \(ACED\) as shown. Let:
\begin{align}
\Gamma &= \text{ circular segment on arc } AE \text{ (one of the dark gray segments)},\\
\Lambda &= \text{ circular segment on arc } AB \text{ (entire colored region, light and dark)}.
\end{align}
Then \(\Gamma\) is less than \(▵EDA,\) which is congruent to \(▵ECA,\) so:
\begin{align}
2 \Gamma & < \Gamma + ▵ECA\\
&= {{1} \over {2}} (2 \Gamma + 2 ▵ECA)\\
&= {{1} \over {2}} \Lambda,
\end{align}
allowing a comparison of \(\Sigma_3\) and \(\Sigma_2:\)
\begin{align}
\Sigma_3 &= 8 \Lambda\\
&= 4(2 \Gamma)\\
& < 4\left({{1} \over {2}} \Lambda\right)\\
&=2 \Lambda\\
&= {{1} \over {2}} \Sigma_2.
\end{align}
The same calculation compares the regular \(16-\)gon to the regular octagon and similarly for all the rest, leading to \(\Sigma_{n+1} < {{1} \over {2}} \Sigma_n\) for all \(n = 2, 3, \ldots.\) The next step is to deploy:
XII.1. Similar polygons inscribed in circles are to one another as the squares on their diameters.
For a modern analyst, the proof is done. For let \(P_n\) be the \(2^n-\)gon inscribed in the original circle \(\Omega,\) as just described, and let \(d\) be the diameter of \(\Omega.\) Let \(\Sigma'_n, P'_n,\) and \(d'\) be similarly defined for a second circle \(\Omega'.\) In modern notation, XII.1 says:
\[{P_n \over d^2} = {P'_n\over d'^2},\tag{14}\]
where \(P_n\) stands for the area of \(P_n\) in such equations and similarly for circles. But \(\Omega = P_n + \Sigma_n,\) where \(\Sigma_n \rightarrow 0,\) so \(P_n \rightarrow \Omega.\) Similarly \(P'_n \rightarrow \Omega'.\) These facts and (14) imply XII.2. But Euclid was not a modern analyst, so let's continue with his proof. There exists an area \(S\) such that:
\[{d^2 \over d'^2} = {\Omega \over S}.\tag{15}\]
The object is to prove \(S = \Omega'.\) For suppose \(S < \Omega'.\) However small \(\Omega' - S\) is, X.1 and the first part of the proof imply that there is an \(n\) such that \(\Omega' - P'_n < \Omega' - S,\) that is, \(S < P'_n.\) Inscribe \(P_n\) in \(\Omega.\) Then:
\[{P_n \over P'_n} = {d^2 \over d'^2} = {\Omega \over S},\tag{16}\]
the first equality by XII.2, the second by (15). Rewrite (16) as:
\[{P_n \over \Omega} = {P'_n \over S},\]
a contradiction because the left side is less than \(1\) and the right side is greater than \(1.\) Therefore, it cannot be the case that \(S < \Omega'.\)
Suppose on the other hand that \(S > \Omega'.\) Inverting 15:
\[{d'^2 \over d^2} = {S \over \Omega}.\]
Let \(T\) be the area such that:
\[{S \over \Omega} = {\Omega' \over T}.\]
Then \(T < \Omega\) and the situation reverts to that when \(S < \Omega'\) with the roles of \(\Omega\) and \(\Omega'\) exchanged. Therefore, the case that \(S > \Omega'\) is also disallowed and the only possible conclusion is that \(S = \Omega'\) and
\[{d^2 \over d'^2} = {\Omega \over \Omega'},\]
as claimed. QED.
Now that's a nice proof. First off, the symmetry between the two circles is leveraged, making Archimedes' circumscribing polygons unnecessary.[17] The approximating polygons are worthy of Jordan or Lebesgue and epsilons and deltas could be employed to satisfy the most exacting analyst.[18] This proof exemplifies the celebrated method of exhaustion, the ancient Greek approach to limiting processes apparently invented by Eudoxus ~370 BC which prefigured calculus. Euclid continues to use exhaustion in Book XII to prove theorems about pyramids, cones, and spheres (for example in XII.18: Spheres are to one another as the cubes on their respective diameters).
The regular dodecahedron is one of five Platonic solids, the term deriving from Plato's ruminations in the Timaeus where he identifies the tetrahedron, octahedron, icosahedron, and cube with fire, air, water, and earth, respectively, saying of the dodecahedron:
There was yet a fifth combination which God used in the delineation of the universe.
So it is fitting that Euclid concludes the Elements by constructing the regular dodecahedron. Some lemmas are needed before proceeding to the proof:
XIII.4. If a straight line is cut in extreme and mean ratio, then the sum of the squares on the whole and on the lesser segment is triple the square on the greater segment.

Proof. "Extreme and mean ratio" means the golden section of II.2, discussed above. Cut segment \(AB\) in golden section at \(C\) and build out the square \(AE\) as shown. Cut segment \(BE\) in golden section at \(K\) as well. II.2 implies that:
\begin{align}
\Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!AK = \Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!CE &= \square HG\\
\therefore \; \Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!AK + \Large \sqsubset\!\!\sqsupset\!\!\!\normalsize\!CE &= 2 \cdot \square HG.\tag{17}
\end{align}
The left side of (17) is the gnomon (the gray L-shaped region) plus \(\square CK,\) so adding \(\square HG\) to both sides of (17) implies that the large square plus the small one is three times the medium sized square:
\[\square AE + \square CK = 3 \cdot HG. \quad \mathbf{QED.}\]
To see this in modern notation, let \(AC = \varphi = (\sqrt{5}+1)/2, CB = 1.\) Then the first line below translates the lemma into modern algebra and the following lines are consequences:
\begin{align}
(\varphi+1)^2 + 1^2 &= 3 \varphi^2\\
(\varphi^2 + 2 \varphi + 1) + 1 &= 3 \varphi^2\\
(\varphi+1) + 2 \varphi + 1 + 1 &= 3 (\varphi+1)\\
3 \varphi+1 &= 3 \varphi+1.
\end{align}
The third line results from putting \(\varphi^2 = \varphi + 1,\) a key identity. These steps are reversible, so the first line is true, which just states the lemma. This one will also be needed:
XIII.5. If a straight line is cut in extreme and mean ratio, and a straight line equal to the greater segment is added to it, then the whole straight line has been cut in extreme and mean ratio, and the original straight line is the greater segment.

Proof. Let \(AB\) be the original straight line cut in golden section at \(C\) with \(AC\) the larger segment. Extend \(AB\) to point \(D\) on the other side of \(C\) and such that \(AD = AC.\) The object is to prove that \(A\) cuts \(DB\) in golden section at \(A\) with \(AB\) being the greater segment. Euclid builds squares and rectangles on the segments and proceeds much like in XIII.4. I'll abbreviate the proof by applying modern algebra. \(AB\) being cut in golden section at \(C\) with \(AC\) the larger segment amounts to \(AC = \varphi, CB = 1,\) as shown in the diagram. Work backwards:
\begin{align}
{{AB} \over {DB}} &= \varphi\\[.5em]
{{2 \varphi + 1} \over {\varphi+1}} &= \varphi\\[.5em]
2 \varphi + 1 &= \varphi (\varphi + 1)\\
&= \varphi^2 + \varphi\\
&= (\varphi + 1) + \varphi\\
&= 2 \varphi + 1.
\end{align}
These steps are reversible, proving the proposition. QED.
XIII.17. To construct a dodecahedron and comprehend it in a sphere, like the aforesaid figures; and to prove that the square on the side of the dodecahedron is the irrational straight line called apotome.
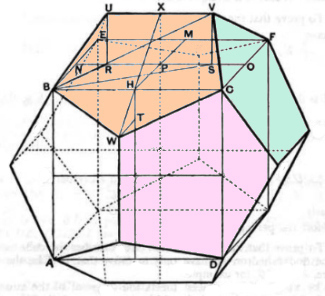
Proof. Inscribe a cube in the given sphere (XIII.15). Each vertex of the cube will be a vertex of the dodecahedron as well. To find the other vertices, build little pup-tents on each face of the cube, as shown.
Start by erecting a pup-tent atop the cube with base \(\square BEFC.\) The question is where to place points \(U\) and \(V\) above the square. That is the only question really, because by the symmetry of the arrangement, all the other vertices of the would-be dodecahedron would then be fixed. To this end, bisect \(EB\) at \(N\) and \(FC\) at \(O.\) Bisect \(NO\) at \(P,\) the center of \(\square BEFC.\) Divide \(PN\) in golden section with \(PR\) being the greater segment. Likewise cut \(PO\) in golden section at \(S\) with \(PS\) the greater segment. Erect \(RU\) directly above \(\square BEFC\) so that \(RU = PR.\) That fixes point \(U;\) and \(V\) and the top edges of the pup-tents on all the other faces are located similarly. All that remains (!) is to prove that the twenty points so determined are all on the sphere and constitute the vertices of a regular dodecahedron. For the second point it is required to prove that the pentagon \(BUVCW\) in the image above to the right is an equilateral, equiangular pentagon in one plane. Take these points in order:
1) All twenty points lie on the sphere.
The vertices of the cube lie on the sphere by construction. It suffices to prove that point \(U\) lies on the sphere, since then \(V\) and all the similarly defined points do as well by the symmetry of the construction. Let \(Z\) be the center of the sphere. Then since \(B\) is a vertex of a cube on the surface of the sphere and \(ZP\) is half the edge of the cube:
\[ZB^2 = 3 ZP^2\tag{18}\]
by two applications of the Pythagorean Theorem. \(R\) cuts \(PN\) in golden section with \(RP\) the greater segment and \(PS = RP\) is added on, the situation in XIII.5, so \(P\) cuts \(NS\) in golden section and:
\begin{align}
ZU^2 &= ZX^2 + XU^2\\
&= NS^2 + PS^2\\
&= 3 PN^2\\
&= 3 ZP^2\tag{19},
\end{align}
the third line following from XIII.4. (18) and (19) imply that \(ZB = ZU,\) that is, \(U\) is on the sphere.

2) Points \(B,U,V,C,W\) all lie in one plane.
\(B,U,V,C\) all lie in one plane by construction. The task is to prove that point \(W\) lies in the same plane and that will be true if \(WHX\) is a straight line. Cut the cube in half with a plane through \(Y, W, H, X,\) the diagram here being in that plane. It's not obvious that \(WHX\) is a straight line, that's what needs to be proven. VI.32 is just what's needed to address this situation. It says that if \(TH \; || \; PX, HP \; || \; WT,\) and \(WT / TH = HP / PX,\) then \(WHX\) is a straight line. \(TH\) and \(PX\) are each parallel to one of the edges of the cube, so they are parallel. \(WT\) and \(HP\) are perpendicular to them respectively, so they are parallel as well. Point \(W\) plays the same role on the front of the figure as point \(U\) on the top, so \(▵WTH \cong ▵URN\) with the points corresponding in that order. It follows that \(▵WTH\) is a golden triangle (that is, the legs are in the golden ratio), with \(WT\) being the greater side. \(PH\) is half the cube's edge, so \(PH = PN.\) Also, \(PX = RU = RP,\) the first equation because both \(PX\) and \(RU\) are the height of the pup-tent and the second one by how point \(U\) was defined. \(PN\) and \(RP\) are in the golden ratio with \(RP\) being the greater segment — that is how \(R\) was defined, so:
\[{{PX} \over{PH}} ={{PX} \over{PN}} ={{RP} \over{PN}}.\]
It follows that \(▵HPX\) is also a golden triangle, so the two triangles are similar and their sides in proportion. The conditions for VI.32 are satisfied, so \(WHX\) is a straight line. Another way of putting this is that, relative to \(\square BEFC,\) the slopes of \(WH\) and \(HX\) are the same, so \(WHX\) is a straight line.
3) The pentagon \(BUVCW\) is equilateral.
By symmetry, all the pentagons will be equilateral if \(BUVCW\) is. The segments \(BU, VC, CW, WB\) are all defined similarly by connecting a vertex of the cube to one of the symmetrically defined points \(U, V, W,\) so the four of them are equal. It remains to prove that the top edge of the pup-tent, \(UV,\) is the same length as the others:
\begin{align}
BU^2 &= BR^2 + RU^2\\
&= (BN^2 + NR^2) + RP^2\\
&= (PN^2 + NR^2) + RP^2\\
&= 3RP^2 + RP^2\\
&= (2RP)^2\\
&= (2UX)^2\\
&= UV^2
\end{align}
Therefore \(UV=BU\) as asserted. The only tricky substitution here is \(PN^2 + NR^2 = 3RP^2,\) which follows from XIII.4.
4) The pentagon \(BUVCW\) is equiangular.
XIII.7 says that if any three angles are equal in an equilateral pentagon, then the pentagon is equiangular. The angles at \(U\) and \(V\) in pentagon \(BUVCW\) were constructed the same way, so they are equal — one of the other angles needs to be the same to invoke XIII.7. It's going to be the angle at \(W,\) shown equal to the angle at \(U\) by proving that \(BC = BV\) and therefore \(▵BCW \cong ▵BVU\) since all the sides of the pentagon are equal:
\begin{align}
BV^2 &= BS^2 + SV^2\\
&= (BN^2 + NS^2) + SP^2\\
&= PN^2 + (NS^2 + SP^2)\\
&= PN^2 + 3PN^2\\
&= 4PN^2\\
\therefore BV &= 2PN = BC.
\end{align}
Here again the key substitution is \(NS^2 +SP^2 = 3PN^2,\) by XIII.4. It follows that the pentagon angle at \(W\) is equal to the angle at \(U\) and therefore the pentagon is equiangular by XIII.7.
So the constructed figure has all its vertices on the sphere and all of its faces are regular pentagons — it is a regular dodecahedron![19] QED.

To coordinatize the construction, start with a cube of edge \(2\) centered at the origin \(K\) with coordinates \((\pm 1, \pm 1, \pm 1).\) The positive \(x-\)axis comes out of the figure parallel to \(PH,\) the positive \(y-\)axis goes to the right parallel to \(NPO,\) and the positive \(z-\)axis goes straight up along \(KPX.\) \(NP\) is cut in golden section at \(R\,\) with \(PR\) the longer segment. Since \(NP = 1,\) this implies \(PR = 1 / \varphi,\) and since \(RU = PR\) by construction, \(RU = 1 / \varphi\) as well. \(RU\) is the height of the pup-tent above the cube, so \(U_z\ = 1 + 1 / \varphi = 1 + (\varphi - 1) = \varphi.\) \(U_y\) is the negative of the length of \(UX,\) which is half the side of the pentagon. The side of the pentagon is in relation to the side of the cube by the golden section, so:
\begin{align}
U_y &= - \small {{1} \over {2}} \normalsize UV\\[.5em]
&= - {{1} \over {2}} \cdot {{2} \over {\varphi}}\\[.5em]
&= -{{1} \over {\varphi}}.
\end{align}
And \(X\) lies straight above the origin along the \(z-\)axis, so \(U_x = 0.\) Since \(V\) is the mirror image of \(U\) through the \(xz\) plane, it can be worked out as well:
\begin{align}
U &= (U_x, U_y, U_z) = (0, - 1/\varphi, \varphi)\\
V &= (V_x, V_y, V_z) = (0, + 1/\varphi, \varphi)
\end{align}
All twenty vertices can be determined similarly:
\begin{align}
(\pm 1, \pm 1, \pm 1)\\
(0, \pm 1/\varphi, \pm \varphi)\\
(\pm \varphi, 0, \pm 1/\varphi)\\
(\pm 1/\varphi, \pm \varphi, 0)
\end{align}
A modern approach might ignore all of Euclid's subtleties and start with these coordinates, using the machinery of 3D analytic geometry and vector calculus to prove they constitute a dodecahedron. The points \(B, U, V, C, W\) could be shown to lie in the same plane, for example, by finding the equation for the plane and showing that the points' coordinates all satisfy it.

There are a number of striking features about this work and its history. Foremost are its longevity and relevance from the start. That this long text and its diagrams have survived probably reasonably intact for a hundred generations speaks eloquently of how highly it was valued at each point in that long chain of transmission. Valued, but also preserved, studied, and mastered (to varying degrees certainly) by people at each link in that chain.
The hallowed mathematical practice of learning by doing is built into the tradition. Geometry especially lends itself to this approach, where a proposition's statement and canonical diagram are the main things to be remembered or transcribed, the proof to be filled in by the learner / performer. The earliest extant fragment from the Elements from ~100 AD, shown here, contains the statement and diagram for Proposition II.5. Both are very close to the Heiberg reconstruction of the oldest Greek manuscripts from the ninth century which apparently trace back to Theon in the fourth century, suggesting strong continuity in the received text and diagrams.[20]

The Elements itself or glosses on it have been a staple of education from the time it was set down — I still have my copy of a detailed foldout chart of the logical dependencies in Book I required by Mr. Vavasseur, S. J., in sophomore year geometry in 1962. British mathematics education even at the higher levels centered around Euclid until around 1900, not always with good effect as it threatened to smother newer voices as it had in the early modern period.[21] Hoping to break this monopoly, Bertrand Russell wrote of Euclid's verbosity, obscurity and pedantry in 1902 and went on to assail his logical integrity ("the value of his work as a masterpiece of logic has been very grossly exaggerated").[22] A more recent deep study of I.2 from the standpoint of computational geometry reaches a different verdict, concluding that "Euclid deserves praise for his brilliance" and that early commentators "missed the essence, semantics, or deep structure behind Euclid's proof."[23]
The Elements is not perfect, as suggested by the robust tradition of explication and amendment over millennia, itself evidence of its continuing mathematical value. The long life and continued interest highlight that the Elements is good mathematics imbued with a deep internal logic not fully revived until the axiomatic approach of twentieth century algebra. The results themselves are foundational and have stood the test of time as documented in this article. The Elements is without peer as the most important, successful, and enduring scientific work of all time. There is only one other book of this antiquity with greater cachet, and that one, it is said, was sent to us by the Lord Himself.
Mike Bertrand
May 20, 2022
^ 1. Encounters with Euclid: How an Ancient Greek Geometry Text Shaped the World, by Benjamin Wardhaugh, Princeton University Press (2021), ISBN 978-0-691-21169-5. See pp. 65-74 for discussion of Erhard Ratdolt, the man and the work, including the first printed edition of the Elements in 1482.This engaging book uses short chapters to illustrate the impact of the Elements down the ages. The "Notes on Sources" are invaluable.
^ 2. See Heath for an extensive account of European editions of Euclid: Euclid's Elements, Volume 1, translated with introduction and commentary by Sir Thomas L. Heath, Dover Publications, Inc. (1956), Chapter VIII, "Principal Translations and Editions of the Elements, pp. 91-113. Erhard Ratdolt published the first printed Latin edition of the Elements in Venice in 1482, pictured at the top of this article. Simon Grynaeus published the first printed Greek edition in Basil in 1533. Tartaglia published the first printed vernacular edition (in the Venetian dialect of Italian) in Venice in 1543.
^ 2a. Newton broke his teeth as a young mathematician by translating key books of Barrow's 1655 edition of Euclid into modern notation — modern even by today's standards. This is known because his copy of Barrow's Euclid is in the library of Trinity College, Cambridge, and it is heavily annotated with his small neat handwriting. See Wardhaugh, pp. 230-235.
^ 3. The first scraps of something recognizably from Euclid date to ~240 BCE, found at Elephantine island at the first cataract of the Nile, probably the work of a garrison soldier rehearsing Book XIII propositions on the icosahedron. Scraps is the right word, the images and text etched on six ostraka (broken pottery shards). See Wardhaugh, pp. 18-25.
^ 3a. The genealogy of the text of the Elements has been of interest to scholars at least since the time of Theon of Alexandria (~ 335 - 405 AD). Theon's edition of the Elements is likely the basis for almost all manuscript editions that have survived, and there are many of them, a testament to the ongoing high esteem for the Elements over the millennia. Theon's daughter was the celebrated mathematician Hypatia. See Wardhaugh, pp. 31-38, for more on Theon and his massive influence on the received text of the Elements.
^ 4. The 1956 edition of Heath comes in three volumes:
• Volume 1: Introduction and Books I - II
• Volume 2: Books III - IX
• Volume 3: Books X - XIII.
^ 5. Euclid: The Creation of Mathematics, by Benno Artmann, Springer (1999), ISBN 0-387-98423-2.
^ 6. All these notations are from Artmann.
^ 7. For Euclid's geometric algebra and the constructions in this section in particular, see A History of Mathematics, by Carl B. Boyer, John Wiley & Sons (1st ed., 1968), ISBN 0-471-09374X, §VII.6, pp. 120-124. Heath also has good discussion in his annotations of II.5 and II.6 and of VI.27 — VI.29.
^ 8. Donald Knuth writes that "[the Euclidean algorithm] is the granddaddy of all algorithms, because it is the oldest nontrivial algorithm that has survived to the present day." See The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 2nd ed., by Donald Knuth, Addison-Wesley (1981), ISBN 0-201-03822-6, p. 318.
^ 9. See "Did Euclid Need the Euclidean Algorithm to Prove Unique Factorization?", by David Pengelley and Fred Richman, The American Mathematical Monthly, 113:3 (2006), pp. 196-205.
^ 10. See Pengelley and Richman, §4, "How to Fix Euclid's Argument", pp. 201-203.
^ 11. See Proofs from THE BOOK, by Martin Aigner and Günter M. Ziegler, Springer (1998), ISBN 3-540-63698-6, Chapter 1. Euclid's proof that there are an infinite number of primes is the very first proof in this book. There are five other proofs, the last of which shows the stronger result that the sum of the reciprocals of all the primes diverges.
^ 12. A Mathematician's Apology, by G. H. Hardy, Cambridge University Press (1940), pp. 18-19.
^ 13. "The Discovery of Incommensurability by Hippasus of Metapontum", by Kurt Von Fritz, Annals of Mathematics, 46:2 (April 1945), pp. 242-264.
^ 14. See Heath, Vol. 3, p.1 for the quote. He discusses the scholia at length in Vol. 1, pp. 64 - 74.
^ 15. The ancient Greeks called the process of X.2 anthyphairesis, "taking away or stealing in turn". See "Incommensurability Proofs: A Pattern That Peters Out", by E. J. Barbeau, Mathematics Magazine, 56:2 (March 1983), pp. 82-90. The term anthyphairesis and its translation is on p. 87.
^ 15a. See Calculus: A Genetic Approach, by Otto Toeplitz, The University of Chicago Press (2007), ISBN-13: 978-0-226-80668-6, p. 12. Toeplitz's book was written in the 1930s but found among his papers at death and first published in German in 1949.
^ 16. Heath's discussion of X.1 and X.2 is most helpful — see Vol. 3, p. 14 ff. Barbeau and Fritz point out that the Euclidean Algorithm can be carried out on the regular pentagon as well, leading to an infinite regress of smaller and smaller pentagons showing that the side and diagonal of a regular pentagon are incommensurable (ie., the golden ratio \(\varphi\) is irrational).
^ 17. See Heath's discussion of XII.2 at Vol. 3, p. 374 ff. Artmann is also on point (pp. 273-274).
^ 18. The epsilon-delta proof of this proposition is actually carried out by Toeplitz on pp. 11-14. Jordan used approximating polygons when first proving the Jordan Curve Theorem — see Cours d'analyse de l'École polytechnique, by Camille Jordan, Vol. 1 (Calcul Différentiel), 2nd ed., Gauthier-Villars et Fils (1893), Part VIII, p. 90ff. Lebesgue used approximating polylines in an elegant proof of the Weierstrass Approximation Theorem in 1898: "Sur l'approximation des fonctions", by H. Lebesgue, Bull. Sci. Math. 22 (1898), pp. 278-287. The French term for the method of exhaustion is méthode des anciens.
^ 19. Heath's commentary on XIII.17 is invaluable and I follow it closely. The apotome is a mysterious notion buried in the profundities of Book X. It is a difference of certain line segments (ἀποτομή, apotome = "cutting off") and in the dodecahedron concerns the relation between the diameter of the circumscribing sphere and the length of the dodecahedron's edges. For a sophisticated account of Book X, see "An Invitation to Read Book X of Euclid's Elements", by David Fowler, Historia Mathematica 19 (1992), pp. 233-264.
^ 20. Euclidis Elementa, Vol. I, by I. L. Heiberg, Teubner (1883), p. 131. The discoverers of the Oxyrhynchus Papyri, Bernard Grenfell and Arthur Hunt, compared the text of II.5 in the papyrus fragment they found with that in the received manuscripts and found them almost identical. See The Mathematics of Plato's Academy: A New Reconstruction, 2nd ed., by David Fowler, Clarendon Press (1999), ISBN 0198502583, p. 8. In 1898, shortly after the discovery, Grenfell and Hunt dated the papyrus to the third or fourth century AD, but an expert papyrologist Fowler consulted dated it with confidence to 75-125 AD (see Fowler, p. 211).
^ 21. See Wardhaugh, pp. 285-290, for an account of of Euclid's dominance in Victorian Britain and the successful challenge to him around 1900.
^ 22. “The Teaching of Euclid”, by Bertrand Russell, The Mathematical Gazette 2 (May 1902), pp. 165-7. The references are to the start and end of this short essay.
^ 23. "A New Look at Euclid's Second Proposition", by Godfried Toussaint , The Mathematical Intelligencer, 15, No. 3 (1993), pp. 12–24. "Euclid deserves praise" : p. 19; "missed the essence" : p. 20.