The Fibonacci Sequence and the Golden Ratio

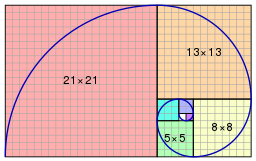
Here is the Fibonacci sequence:

\( 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, \ldots. \)

Call the first element \( u_1, \) the second one \( u_2, \) the third \( u_3, \) and so on. The sequence starts with two ones, then each subsequent element is the sum of the two preceding ones:

\begin{align}
u_1 &= u_2 = 1\\
u_{n+2} &= u_{n+1} + u_{n}, \hspace{15px} n \geq 1.
\end{align}

Consider these facts:

\begin{align}
(3/2) \cdot u_n &\leq u_{n+1} \leq (2/1) \cdot u_n, \hspace{15px} n \geq 1, \\
(8/5) \cdot u_n &\leq u_{n+1} \leq (5/3) \cdot u_n, \hspace{15px} n \geq 4. \\
\end{align}

These formulas and similar ones can be proven by induction, walking up the sequence for the constants. It turns out that as \( n \) increases, \( u_{n+1}/u_n \) oscillates around a fixed value, which they approach ever more closely. That is, \( u_{n+1}/u_n \) converges as \( n \rightarrow \infty. \) Assuming convergence to some fixed nonzero value \( \varphi \) (proof below), a simple calculation shows its value:

\begin{align}
u_{n+2} &= u_{n+1} + u_n\\[1.5ex]
{u_{n+2} \over u_{n+1}} &= 1 + {u_n \over u_{n+1}}\\
\varphi &= 1 + {1 \over \varphi}\\
\varphi^2 &= \varphi + 1.
\end{align}

The second line leads to the third by taking the limit. The last line is a quadratic equation in \( \varphi \) which has two real roots:

\begin{align}
\varphi &= {{1 + \sqrt{5}} \over 2} = 1.618034\ldots,\\
\varphi' &= {{1 - \sqrt{5}} \over 2} = -0.618034\ldots.
\end{align}

The positive root is the one we're looking for, so \( \lim_{n \rightarrow \infty} (u_{n+1} / u_n) = \varphi, \) the Golden Ratio or the Golden Section and one of the most well-known constants in mathematics. Because \( \varphi \) and \( \varphi' \) are roots of the same quadratic equation, we have some simple relations between them:

\begin{align}
x^2 - x - 1 &= (x - \varphi)(x - \varphi') = x^2 - (\varphi + \varphi')x + \varphi \varphi'\\
\therefore \varphi + \varphi' &= 1 \; \text{ and } \; \varphi \varphi' = -1.
\end{align}

We want to find a formula for the \(n\)^th Fibonacci number. To this end, consider the following statements, the first from the definition of \( \varphi \) and then multiplying by \( \varphi \) at each step:

\begin{align}
\varphi^2 &= \varphi + 1\\
\varphi^3 &= \varphi^2 + \varphi\\
\varphi^4 &= \varphi^3 + \varphi^2\\
\varphi^5 &= \varphi^4 + \varphi^3\\
&\vdots
\end{align}

These expressions imply that \( S_1 = \{1, \varphi, \varphi^2, \varphi^3, \varphi^4, \varphi^5, \ldots \} \)is a Fibonacci-like sequence, in that every element from the third on is the sum of the two previous elements. It differs from the standard Fibonacci sequence by starting with \( (1, \varphi) \) instead of \( (1, 1), \) and of course the values are not integers (amazingly enough, they approach integers as \( n \) increases). The same argument applies to \( \varphi'. \) It's clear that a linear combination of two Fibonacci-like sequences is also a Fibonacci-like sequence, a fact easily proven by induction. A "linear combination" of two sequences \( S_1 \) and \( S_2 \) is the sequence \( S = aS_1 + bS_2, \) where \( a \) and \( b \) are fixed real numbers and each element in \( S \) is the linear combination of the corresponding elements in \( S_1 \) and \( S_2. \) So put:

\begin{align}
S_1 &= \{ \varphi^n \}_{n=0}^{\infty} = \{1, \varphi, \varphi^2, \varphi^3, \varphi^4, \varphi^5, \ldots \}\\[1.5ex]
S_2 &= \{ \varphi'^n \}_{n=0}^{\infty} =\{1, \varphi', \varphi'^2, \varphi'^3, \varphi'^4, \varphi'^5, \ldots \}\\[1.5ex]
S &= a S_1 + b S_2
\end{align}

and find \( a \) and \( b \) such that the first two elements of \( S \) are the first two Fibonacci numbers, namely \( 1 \) and \( 1: \)

\begin{align}
1 &= a \cdot 1 + b \cdot 1\\
1 &= a \cdot \varphi + b \cdot \varphi'
\end{align}

This is a system of two equations in two unknowns \( a \) and \( b.\) Solving results in:

\begin{align}
a &= {\varphi \over \sqrt{5}},\\[1.5ex]
b &= {-\varphi' \over \sqrt{5}},
\end{align}

which leads to:

\begin{align}
u_n &= a \varphi^{n-1} + b \varphi'^{n-1}\\[1.5ex]
&= \left({\varphi \over \sqrt{5}}\right) \cdot \varphi^{n-1} - \left({\varphi' \over \sqrt{5}}\right) \cdot \varphi'^{n-1}\\[1.5ex]
&= {\varphi^n \over \sqrt{5}} - {\varphi'^n \over \sqrt{5}}.
\end{align}

The key point is that \( S \) is a Fibonacci-like sequence whose first two elements are \( 1 \) and \( 1, \) so it must be the Fibonacci sequence.

This is the Binet formula giving the Fibonacci numbers as powers of \( \varphi \) and \( \varphi' \). The dominant term is \( \varphi^n / \sqrt{5}, \) which approaches the approximated Fibonacci number closer and closer as \( n \) increases. The second term is the adjustment, negative and positive in turns, which approaches zero. It is amazing that such a complex formula involving \( \sqrt{5} \) produces integers, much less the Fibonacci numbers. \( \sqrt{5} \) plays the role of a book-keeping mechanism, collecting integer parts just right and so that the terms involving \( \sqrt{5} \) cancel in the end. Here are the two key formulas derived so far:

\[ \lim_{n \to \infty} {u_{n+1} \over u_n} = {{1 + \sqrt{5}} \over 2} \]

\[ u_n = {1 \over \sqrt{5}} \left( {1 + \sqrt{5} \over 2} \right) ^n - {1 \over \sqrt{5}} \left( {1 - \sqrt{5} \over 2} \right) ^n, \hspace{20pt} n \geq 1 \]

4) Fibonacci Formulas.

There are thousands of Fibonacci formulas, many proved by induction. Consider this:

\begin{align}
1 + 1 &= 2\\
1 + 1 + 2 &= 4\\
1 + 1 + 2 + 3 &= 7\\
1 + 1 + 2 + 3 + 5 &= 12\\
\end{align}

It seems that the sum of the Fibonacci numbers up to a certain point equals the Fibonacci number two further minus one. This is indeed the case. Or this:

\begin{align}
1^2 &= 1 \cdot 2 - 1\\
2^2 &= 1 \cdot 3 + 1\\
3^2 &= 2 \cdot 5 - 1\\
5^2 &= 3 \cdot 8 + 1,\\
\end{align}

also true in general. Here are these two formulas in mathematical notation:

\[ \sum_{k=1}^{n} u_k = u_{n + 2} - 1 \]

\[ u_n^2 = u_{n - 1} u_{n + 1} + (-1)^{n - 1} \]

5) The Golden Section.

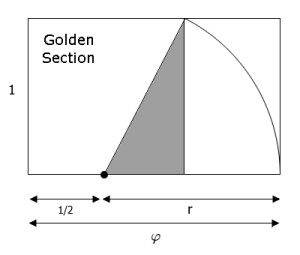
A Golden Rectangle has sides in proportion \( \varphi \) : 1. Construct as follows. Start with a square of side 1 and bisect the bottom edge into two parts of length 1/2. Draw a circle centered at the point of bisection going through the upper right corner. Extend the bottom edge of the square to the right to intersect the circle and build a rectangle as shown to the right of the square. The width of the larger rectangle is \( \varphi. \) To see this, apply the Pythagorean Theorem to the shaded triangle:

\begin{align}
r^2 &= (1/2)^2 + 1^2\\
&= 5/4\\
r &= \sqrt{5} / 2\\
\text{ width } &= r + 1/2 = {{\sqrt{5} + 1} \over 2} = \varphi.
\end{align}

There is more — the smaller rectangle just tacked on to the right of the square is also a golden rectangle! This is because its dimensions are \( 1 : (\varphi - 1) \) and these two equations are equivalent:

\begin{align}
{1 \over {\varphi - 1}} &= \varphi\\
\varphi^2 - \varphi - 1 &= 0.
\end{align}

Consider the isosceles triangle with base angles \( \angle A = \angle B = 2 \pi / 5 = 72^{\circ}. \) Let \( \overline{AB} = 1 \) and \( \overline{AC} = \overline{BC} = d. \) Bisect \( \angle A \) into two \( 36^{\circ} \) angles and let the bisector intersect \( BC \) at point \( D. \) \( \bigtriangleup \! BDA \) is similar to the large triangle and \( \overline{AD} = 1, \) since \( \bigtriangleup BDA \) is iosceles. \( \bigtriangleup \! CAD \) is also isosceles, so \( \overline{CD} = \overline{AD} = 1. \) Since \( \bigtriangleup \! BDA \sim\ \!\!\bigtriangleup \! ABC: \)

\begin{align}
{\overline{BD} \over \overline{AB}} &= {\overline{AB} \over \overline{AC}}\\[1.5ex]
{{d - 1} \over 1} &= {1 \over d}\\[1.5ex]
\therefore d^2 - d &= 1\\[1.5ex]
d^2 - d - 1 &= 0.
\end{align}

That is, \( d = \varphi, \) proving that the sides of the \( 36^{\circ}-72^{\circ}-72^{\circ} \) triangle are in the ratio \( \varphi : 1 \) and that the \( 36^{\circ}-72^{\circ}-72^{\circ} \) triangle is constructible with straightedge and compass.

Next circumscribe a circle around the \( 36^{\circ}-72^{\circ}-72^{\circ} \) triangle. Since segment \( AB \) subtends an angle of \( 36^{\circ} \) at opposite point \( C \) on the circle, \( AB \) marks off one fifth of a circle (twice \( 36^{\circ} \) or \( 72^{\circ} \)). Mark off \( BD \) and \( AE \) of length \( \overline{AB} \) as shown and connect \( EC \) and \( DC \) to make a regular pentagon. This shows that the regular pentagon is constructible with straightedge and compass and that its diagonal and side are in the ratio \( \varphi : 1. \) I've got more on the regular pentagon here.

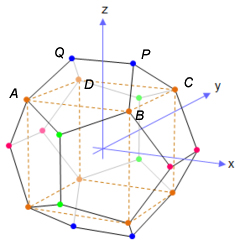
The regular dodecahedron, much beloved by the ancient Greeks and taken up at the end of Euclid's Elements, is also implicated (image courtesy of Wikepedia). Its twenty corners are given by these Cartesian coordinates in an \( xyz \) system, where the edge length is \( 2/\varphi = \sqrt{5}–1 \) and the circumscribing sphere has radius \( \sqrt{3}: \)

\begin{align}
(\pm 1, \ \pm 1, \ \pm 1) \; \; \color{orange}{\bullet}\\
(0, \ \pm \varphi, \ \pm 1/\varphi) \; \; \color{green}{\bullet}\\
(\pm 1/\varphi, \ 0, \ \pm \varphi) \; \; \color{blue}{\bullet}\\
(\pm \varphi, \ \pm 1/\varphi, \ 0) \; \; \color{pink}{\bullet}
\end{align}

To see this, start with a cube with coordinates \( (\pm 1, \ \pm 1, \ \pm 1), \) with edges the orange dashed lines and vertices the orange points in the Wikipedia image. The vertices of the cube are going to be on the dodecahedron. If \( r \) is the radius of the circumscribing sphere, then \( r^2 = 1^2 + 1^2 + 1^2 = 3, \) so \( r = \sqrt{3}. \) The edges of the cube are diagonals of the pentagonal faces, so those pentagons have sides of length \( 2 / \varphi. \) Consider square \( ABCD, \) the top face of the cube, and the little pup-tent arrangement rising above it peaking at edge \( PQ. \) This is how Euclid constructed the regular dodecahedron in Book XIII, Proposition 17. We want to know the coordinates of point \( P. \) Segment \( QP \) is parallel to the \( x-\)axis and directly above it, so \( P \) has \( y \) coordinate zero. The \( z-\)axis bisects seqment \( QP \) and is perpendicular to it, so the \( x \) coordinate of point \( P \) is \( 1/2 \cdot 2 / \varphi = 1 / \varphi. \)

The harder calculation is the \( z \) coordinate of \( P, \) which depends on the height of the pup-tent above the cube. \( ABPQ \) is a trapezoid that is part of a pentagonal face, as shown here. Drop a line down the trapezoid from \( P \) perpendicular to \( AB \) and let this line intersect \( AB \) at point \( R. \) Finding \( k = \overline{PR} \) will be key to calculating the height of the tent. Imagine cutting segment \( RB \) out out of \( AB \) and also a mirroring segment of the same length at the left of \( AB. \) What is left is a segment directly below \( QP \) and parallel to it. If \( j = \overline{RB}, \) it follows that:

\begin{align}
2 &= \overline{AB}\\
&= 2j + \overline{QP}\\
&= 2j + 2 / \varphi.\\
\therefore 1 &= j + 1 / \varphi\\
j &= 1 - 1 / \varphi = 2 - \varphi,
\end{align}

the last equality being equivalent to \( \varphi^2 = \varphi + 1. \) An identity needed for the next step derives from \( 1 / \varphi = \varphi - 1 : \)

\begin{align}
\left({2 \over \varphi}\right)^2 &= \left(2 \cdot {1 \over \varphi}\right)^2 \\
&= \left( 2 \left( \varphi - 1 \right) \right)^2\\
&= 4 \left( \varphi^2 - 2 \varphi + 1 \right)\\
&= 4 \left( \left( \varphi + 1 \right) - 2 \varphi + 1 \right)\\
&= 4 \left( 2 - \varphi \right).
\end{align}

Now calculate \( k^2 = \overline{PR}^2 \) by applying the Pythagorean Theorem to \( \bigtriangleup \! PRB : \)

\begin{align}
k^2 &= \left({2 \over \varphi}\right)^2 - j^2\\
&= 4 \left( 2 - \varphi \right) - \left( 2 - \varphi \right)^2\\
&= \left(8 - 4 \varphi\right) - \left( 4 - 4 \varphi + \varphi^2 \right)\\
&= 4 - \varphi^2\\
&= 4 - (\varphi + 1)\\
&= 3 - \varphi.
\end{align}

Drop a perpendicular line down from point \( P \) to the square, denoting the distance from \( P \) to the square by \( h. \) That perpendicular line and \( RP \) form part of a right triangle, the third side lying entirely in the square and having length one (that is because \( P \) lies directly above a bisector of the square, which has side two). Applying the Pythagorean Theorem to that triangle results in:

\begin{align}
h^2 &=k^2 - 1\\
&= (3 - \varphi) - 1\\
&= (2 - \varphi) + (\varphi^2 - \varphi -1)\\
&= \varphi^2 - 2 \varphi + 1\\
&= \left( \varphi - 1 \right)^2\\
\therefore h &= \varphi - 1.
\end{align}

\( h \) is just the height of the tent above the square, so the \(z-\)coordinate of \( P \) is:

\[ z = h + 1 = (\varphi - 1) + 1 = \varphi. \]

So \( P = (1/\varphi, 0, \varphi) \) and the twelve vertices of the dodecahedron not on the cube are all along the top edge of a tent above one of the cube faces and submit to a similar analysis. \( Q \) is the mirror image of \( P \) through the \( z-\)axis, for example, so \( Q = (-1/\varphi, 0, \varphi). \)

\( P, Q, \) and their matching vertices on the other side of the dodecahedron (the blue points in the image above) form a rectangle with side lengths in the ratio:

\begin{align}
\text{ ratio } &= {{2 \varphi} \over {2/\varphi}}\\
&= \varphi^2\\
&= \varphi + 1.
\end{align}

There are six such rectangles interior to the dodecahedron.

---

^ Update (Jan 6, 2014): Proceed as follows to prove that the ratios \(u_{n + 1}/u_n\) have a limit as \(n \to \infty\). Let \(\varphi_n = u_{n + 1}/u_n\):

\[ \varphi_n = {{1 \over 1}, {2 \over 1}, {3 \over 2}, {5 \over 3}, {8 \over 5}, {13 \over 8}, {21 \over 13}, {34 \over 21}} \dots \]

First show that \(1 \leq \varphi_n \leq 2\). This is evidently true for the first few elements of the sequence, so assume true for some value of n. Then:

\[ \varphi_{n+1} = {u_{n+2} \over u_{n+1}} = {{u_{n+1}+u_n} \over u_{n+1}} = 1 + {u_n \over u_{n+1}} = {1 + {1 \over \varphi_n}} \]

Taking reciprocals of the inductive hypothesis and then adding 1 gives:

\[ {1 \over 2} \leq {1 \over \varphi_n} \leq 1 \]

\[ {3 \over 2} \leq {1 + {1 \over \varphi_n}} \leq 2 \]

Thus \(1 \leq \varphi_{n+1} \leq 2\), and the result follows for all n.

The fractions jump around when advancing through the sequence, but look at every other one: \(\varphi'_n = 1/1, 3/2, 8/5, 21/13 , \dots \). They are monotonically increasing, at least the first few, eg.:

\[ \varphi_5 = {8 \over 5} < {21 \over 13} = \varphi_7 \]

\[ 104 = {8 \cdot 13} < {5 \cdot 21} = 105 \]

The difference of one between the two products pops out and in fact this is always the case:

\[ {u_k \cdot u_{k + 3}} - {u_{k + 2} \cdot u_{k + 1}} = -1, \hspace{20pt} k \text{ even} \]

We'll prove the more general result:

\[ {u_k \cdot u_{k + 3}} - {u_{k + 2} \cdot u_{k + 1}} = {(-1)}^k, \hspace{20pt} k \geq 1 \hspace{60pt} \text{(1)} \]

which proves not only that \(\varphi'_n\) is monotonically increasing, but also that the subsequence interspersed with that one, \(\varphi''_n = 2/1, 5/3, 13/8, 34/21 , \dots \), is monotonically decreasing. So assume the inductive hypothesis (1) for some k. Then expanding the first term \(u_k\):

\[ {{(u_{k + 2} - u_{k + 1})} \cdot u_{k + 3}} - {u_{k + 2} \cdot u_{k + 1}} = {(-1)}^k \]

\[ { {u_{k + 2} \cdot u_{k + 3}} - {u_{k + 1} \cdot u_{k + 3}} - {u_{k + 2} \cdot u_{k + 1}}} = {(-1)}^k \]

\[ {{u_{k + 2} \cdot u_{k + 3}} - {u_{k + 1} \cdot {(u_{k + 3} + u_{k + 2})}}} = {(-1)}^k \]

Substituting \(u_{k + 4}\) for \(u_{k + 3} + u_{k + 2}\) and rearranging a bit gives:

\[ {-{u_{k + 1} \cdot u_{k + 4}} + {u_{k + 2} \cdot u_{k + 3}} } = {(-1)}^k \]

Multiplying through by -1 gives (1) with k + 1 instead of k, completing the proof of (1). So \(\varphi'_n\) is increasing and bounded above by 2, hence has a limit less than or equal to 2. Similarly \(\varphi''_n\) is decreasing and bounded below by 1, so has a limit greater than or equal to 1.

(1) compares two fractions from \(\varphi_n\) that are two apart. There is also a relation for adjacent elements of \(\varphi_n\) exemplified by:

\[ \varphi_7 = {21 \over 13} < {34 \over 21} = \varphi_8 \]

\[ 441 = {21^2} < {13 \cdot 34} = 442 \]

The formula is the one mentioned at the end of section 4 above:

\[ u_n^2 = u_{n - 1} u_{n + 1} + (-1)^{n - 1} \]

and is proven by induction similarly to (1). Therefore, for any two adjacent fractions \(\varphi_n\) and \(\varphi_{n + 1}\):

\[ {\varphi_{n + 1} - \varphi_n} = {{u_{n + 2} \over u_{n + 1}} - {u_{n + 1} \over u_n} = { {u_{n + 2} \cdot u_n - u_{n + 1} ^2} \over {u_{n + 1} \cdot u_n } } } = { {(-1)}^{n + 1} \over {u_{n + 1} \cdot u_n }} \rightarrow 0 \text{ as } n \rightarrow \infty \]

For odd n, \(\varphi_{n + 1}\) is an element of the decreasing sequence \(\varphi''_n\) and \(\varphi_n\) is the analogous element of the increasing sequence \(\varphi'_n\) and they are as close as you like, but with the first greater than the second. This shows that all the elements of \(\varphi'_n\) are less than all those of \(\varphi''_n\) and that their limits are the same. That is, the original sequence \(\varphi_n\) has a limit. QED