The Origin of the Prime Number Theorem — Legendre and Gauss

The prime numbers have been an object of fascination for a long time. These are the counting numbers having no divisors other than one and themselves:
\[ 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, \ldots. \]
The key fact about the primes is that every natural number can be written as a product of primes, and the product is unique up to the order of the factors. Euclid proved that there are infinitely many prime numbers in 300 BC in Book IX, Proposition 20 of the Elements. Like all of Euclid, the proof is geometrical, with line segments representing numbers, but it's valid and recognizable. The modern proof goes like this:
Theorem. There are infinitely many prime numbers.
Proof. Suppose \( p_1, p_2, \ldots p_n \) represent the first \( n \) prime numbers: \( p_1 = 2, p_2 = 3, p_3 = 5, \) and so on. Then every prime divisor of \( m = p_1 \cdot p_2 \cdot p_3 \cdots p_n + 1 \) is different from \( p_1, p_2, \ldots p_n, \) so there is at least one more prime. Take \( p_1 \) for example. Obviously \( p_1 | (p_1 \cdot p_2 \cdot p_3 \cdots p_n), \) so if \( p_1 | m, \) then \( p_1 | (m - p_1 \cdot p_2 \cdot p_3 \cdots p_n). \) That is, \( p_1 | 1 \) and therefore \( p_1 = 1, \) which is not a prime number. It follows that \( p_1 \) cannot divide \( m \) and similarly none of the \( p_j \) can divide \( m, \) all of whose prime divisors must therefore be other than \( p_1, p_2, \cdots p_n. \)QED.
This proof assumes that every natural number has at least one prime divisor, but this can be filled in. Note that (despite a promising start), \( m = p_1 \cdot p_2 \cdot p_3 \cdots p_n + 1 \) is not necessarily prime itself, it just has a prime factor other than \( p_1, p_2, \ldots p_n: \)
\begin{align}
2 + 1 &= 3\\
2 \cdot 3 + 1 &= 7\\
2 \cdot 3 \cdot 5 + 1 &= 31\\
2 \cdot 3 \cdot 5 \cdot 7 + 1 &= 211\\
2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 + 1 &= 2311\\
2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 + 1 &= 30031 = 59 \cdot 509.\\
\end{align}
The first five values of \( m \) here actually are prime, but the last one is not, its factorization producing two new primes beyond \( 2, 3, 5, 7, 11, 13 \) — namely, \( 59 \) and \( 509. \)
The density of the primes within the stream of integers oscillates wildly and seemingly without pattern. There are fourteen primes between 500 and 600, for example, with 521 being prime, 522 not prime (composite), 523 prime, followed by 17 composites in a row before the next prime at 541. There are 25 primes between 1 and 100, and the primes do seem to thin out on average as one proceeds to greater values. Define the prime counting function \( \pi(x) \) as the number of primes less than or equal to the positive real number \( x, \) so the remarks above can be reframed as:
\begin{align}
\pi(600) - \pi(500) &= 14,\\
\pi(540) - \pi(523) &= 0,\\
\pi(100) &= 25.
\end{align}
Legendre speculated based on a meticulous examination of prime tables available to him in 1808 that:[1]
\[ \pi(x) \approx \text{ leg}(x) := { x \over {\log(x) - 1.08366}}, \]
where \( \approx \) means "is approximately equal to" and where \( \log{x} \) is the natural logarithm of \( x, \) that is, the power of \( e \) that \( x \) is. So, for example:
\begin{align}
\pi(100) &\approx {100 \over {\log(100) - 1.08366}}\\[1.5ex]
&= {100 \over {4.60517 - 1.08366}}\\[1.5ex]
&= {100 \over 3.52151}\\[1.5ex]
&= 28.40
\end{align}
This differs from the actual value of \( \pi(100) = 25 \) by a relative error of 13%, which isn't too bad, but isn't particularly impressive either. In fact the match is uncannily good over the first million integers when approximating \( \pi(x) \) by \( \text{ Leg}(x) = \text{ round(leg}(x)), \) where round() rounds to the nearest integer:
| \(\hspace{20px}x\) | \( \text{ Leg }(x)\) | \( \pi(x)\) | \(\hspace{20px}x\) | \( \text{ Leg }(x)\) | \( \pi(x)\) |
| 10000 | 1231 | 1229 | 350000 | 29961 | 29977 |
| 20000 | 2268 | 2262 | 400000 | 33854 | 33860 |
| 30000 | 3252 | 3245 | 450000 | 37709 | 37706 |
| 40000 | 4205 | 4203 | 500000 | 41533 | 41538 |
| 50000 | 5136 | 5133 | 550000 | 45327 | 45322 |
| 60000 | 6049 | 6057 | 600000 | 49096 | 49098 |
| 70000 | 6950 | 6935 | 650000 | 52841 | 52831 |
| 80000 | 7838 | 7837 | 700000 | 56565 | 56543 |
| 90000 | 8718 | 8713 | 750000 | 60269 | 60238 |
| 100000 | 9588 | 9592 | 800000 | 63955 | 63951 |
| 150000 | 13844 | 13848 | 850000 | 67625 | 67617 |
| 200000 | 17982 | 17984 | 900000 | 71279 | 71274 |
| 250000 | 22035 | 22044 | 950000 | 74918 | 74907 |
| 300000 | 26024 | 25997 | 1000000 | 78543 | 78498 |
Legendre has this table up to 400,000 except for a few small errors. There are many exact matches between \( \text{ Leg}(x) \) and \( \pi(x) \) over the first million integers, even short runs (to be expected considering that \( \text{ leg}(x) \) grows smoothly and \( \pi(x) \) in jerks). For example:
\[ \text{ Leg}(x) = \pi(x) = 72,634, \text{ for } 918,592 \leq x \leq 918,604. \]
In his famous letter to Encke[2] of Christmas Eve, 1849, the 72 year old Gauss relates how as a boy he calculated the density of the primes in blocks of a thousand and how this became a lifelong pastime and led to a conjecture:
My distinguished friend,
Your remarks concerning the frequency of primes were of interest to me in more ways than one. You have reminded me of my own endeavors in this field which began in the very distant past, in 1792 or 1793, after I had acquired the Lambert supplements to the logarithmic tables. Even before I had begun my more detailed investigations into higher arithmetic, one of my first projects was to turn my attention to the decreasing frequency of primes, to which end I counted the primes in several chiliads (thousands) and recorded the results on the attached white pages. I soon recognized that behind all of its fluctuations, this frequency is on the average inversely proportional to the logarithm, so that the number of primes below a given bound n is approximately equal to \[\int {dn \over \log{n}},\] where the logarithm is understood to be hyperbolic.[3]
| chiliad | #primes |
|---|---|
| 991 | 71 |
| 992 | 79 |
| 993 | 65 |
| 994 | 68 |
| 995 | 78 |
| 996 | 69 |
| 997 | 69 |
| 998 | 83 |
| 999 | 74 |
| 1000 | 65 |
By "hyperboloic logarithm", Gauss means the natural logarithm — the area under a hyperbola! In his published Nachlass (papers found after death), Gauss lists the number of primes in every chiliad up to one million. His figures for the last ten chiliads, shown here, are correct — there are exactly 71 primes between 990,000 and 991,000, for example, and 721 primes between 990,000 and 1,000,000, adding up the ten chiliads on the list. So on average, there are 72.1 primes per chiliad just before 1,000,000. Compare to \( 1 / \log{(995,000)} = 0.0724, \) predicting about 72.4 primes per chiliad in this range by Gauss's hypothesis. The man was on to something. In the words of L. J. Goldstein:
Gauss' calculations are awesome to contemplate, since they were done long before the days of high-speed computers. Gauss' persistence is most impressive. ... In spite of these (remarkably few) errors, Gauss' calculations still provide overwhelming evidence in favor of the prime number theorem. Modern students of mathematics should take note of the great care with which data was compiled by such giants as Gauss. Conjectures in those days were rarely idle guesses. They were usually supported by piles of laboriously gathered evidence.[4]
The Fundamental Theorem of Calculus states that for a differentiable function \( f(x): \)
\[ \int_a^b f'(t) dt = f(b) - f(a). \]
That is, integrate the rate of change of a function to find its difference over a range. Obviously \( \pi(x) = \text{ number of primes } \leq x \) isn't differentiable, but Gauss is using the basic concept to suggest that:
\begin{equation}{\int_a^b {dt \over \log{t}} \approx \pi(b) - \pi(a),}\tag{1} \end{equation}
where \( \approx \) means "is approximately equal to". Put \( a = 2, \; b = x \) in (1) and leave off the \( \pi(2) = 1, \) which won't affect the outcome in the limit, to get:
\begin{equation}{\int_2^x {dt \over \log{t}} \approx \pi(x).}\tag{2} \end{equation}
(2) is in fact the celebrated Prime Number Theorem when \( \approx \) is replaced by \( \sim, \) meaning that the ratio of the two sides of (2) has the limit \( 1 \) as \( x \rightarrow \infty. \) The Prime Number Theorem was proven in 1896 by Hadamard and de la Vallée Poussin using complex analysis and by Erdős and Selberg in 1948 using elementary methods (that is, without appeal to complex analysis).
Between one million and three million, Gauss created tables like this one, which shows the distribution of primes in centuries between 1,000,000 and 1,100,000, taking a century as a block of 100 integers starting at a multiple of 100. Each column counts centuries in a myriad (a block of 10,000 integers starting at a multiple of 10,000), so the column under 0 counts centuries between 1,000,000 and 1,010,000, the column under 1 counts centuries between 1,010,000 and 1,020,000, and so on. The numbers along the left indicate how many centuries in the given myriad contain that many primes. The 1 at the top left just inside the table proper indicates that there is one century between 1,000,000 and 1,010,000 containing exactly one prime. The two blanks below it indicate that there are no centuries between 1,000,000 and 1,010,000 containing either two or three primes. The 2 underneath the two blanks indicates that there are two centuries between 1,000,000 and 1,010,000 containing exactly four primes, and so on.
Since each column in the body of the table counts centuries in a myriad, each of those columns sums to 100. The numbers along the bottom count the number of primes in the myriad; for the first column, for example:
\begin{align} \# \text{ primes in the myriad} &= \sum \# (\text{centuries with a given number of primes}) \cdot (\text{that number of primes})\\
&= 1 \cdot 1 + 2 \cdot 4 + 11 \cdot 5 + \ldots + 1 \cdot 12 + 1 \cdot 13\\
&= 752.
\end{align}
The far right column counts centuries in the entire block of 100,000, so that column sums to 1,000 and the value at the bottom right corner, 7210, counts the number of primes in the entire block of 100,000: it results from a calculation similar to the one immediately above and also equals the sum of the values to its left along the bottom of the table.
I checked the first column by hand against a list of the primes between 1,000,000 and 1,100,000, much as Gauss did, and also with a PHP program. The list is a massaged version extracted from Chris Caldwell's list of the first million primes. There are three small errors in the first column: the correct values are 13 centuries containing 6 primes, not 14; and 27 centuries containing 7 primes, not 26 — the other century counts in the first column are correct. This makes the number at the lower left off by one: the correct value is that there are 753 primes between 1,000,000 and 1,010,000, not 752. This can be checked at WolframAlpha with the command pi(1,010,000)-pi(1,000,000).
I haven't checked the other myriads, but did use the same program to check the column on the far right listing the centuries in the entire block of 1,000,000 to 1,100,000. The correct values, listing them horizontally, are:
\[ 1, 4, 21, \color{red}{53}, \color{red}{115}, \color{red}{170}, 217, 164, \color{red}{125}, \color{red}{73}, 39, 12, 6, \color{red}{7216} \]
That is, Gauss's prime count for the block was off, \( \color{red}{7216} \) being the correct value for the number of primes between 1,000,000 and 1,100,000. Note his statement at the bottom that:
\[ \int {dx \over \log{x}} = 7212.99. \]
His point is that this definite integral, taken from 1,000,000 to 1,100,000, is approximately equal to the number of primes between 1,000,000 and 1,100,000. Gauss no doubt used Simpson's Rule to calculate the integral, which gives \( \int {dx / \log{x}} = 7212.99438, \) the correct value being \( 7212.99426 \)
In the letter, Gauss goes on to discuss Legendre's formula and expresses skepticism about the constant in the denominator, noting that the formula becomes less accurate the higher you go.
The Prime Number Theorem states that:
\begin{equation}{ \pi(x) \sim \int_2^x {dt \over \log{t}}, }\tag{2'} \end{equation}
meaning that the ratio of the two sides of (2') goes to \( 1 \) as \( x \rightarrow \infty. \) The right side of (2') is called the logarithmic integral, denoted by \( \text{ Li}(x). \) Sometimes the PNT is stated as:
\begin{equation}{ \pi(x) \sim {x \over \log{x}}, }\tag{3} \end{equation}
and (2') and (3) are equivalent:[5]
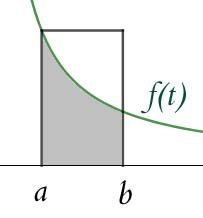
Theorem. Put \( \text{ Li}(x) := \int_2^x {dt \over \log{t}}, \;\; A(x) := {x \over \log{x}}. \) Then as \( x \rightarrow\ \infty, {\pi(x) \over {\text{ Li}(x)}} \rightarrow 1 \) if and only if \( {\pi(x) \over A(x)} \rightarrow 1. \)
Proof. Integrate \( \text{ Li}(x) \) by parts with \( v = {1 \over \log{t}}, \; du = dt \) to get:\begin{equation}{ \text{ Li}(x) = {x \over \log{x}} - {2 \over \log{2}} + \int_2^x {dt \over \log^2{t}}.}\tag{4} \end{equation}
For \( x \geq 4, \) the definite integral at the end of (4) can be broken into two pieces:
\begin{align}
\int_2^x {dt \over \log^2{t}} &= \int_2^{\sqrt{x}} {dt \over \log^2{t}} + \int_{\sqrt{x}}^x {dt \over \log^2{t}}\\[1.5ex]
&\leq \sqrt{x} \cdot {1 \over \log^2{2}} + x \cdot {1 \over \log^2{\sqrt{x}}}.\tag{5}
\end{align}Each integral on the right is less than or equal to the expression beneath it, since \( 1 \over \log^2{t} \) is monotonically decreasing for \( t \geq 2, \) so the principle in the box applies. Combining (4) and (5):
\begin{align}
\text{ Li}(x) - A(x) &\leq -{2 \over \log{2}} + {\sqrt{x} \over \log^2{2}} + {x \over \log^2{\sqrt{x}}}\\[2.0ex]
\therefore \left|{{\text{ Li}(x)} \over A(x)} - 1\right| &\leq \left|{-{2 \over \log{2}} + {\sqrt{x} \over \log^2{2}} + {x \over \log^2{\sqrt{x}}} \over A(x)}\right|\\[2.0ex]
& \leq {\log{x} \over x} \cdot \left({2 \over \log{2}} + {\sqrt{x} \over \log^2{2}} + {x \over \log^2{\sqrt{x}}}\right)\\[2.0ex]
&= {{2 \over \log{2}} \cdot {\log{x} \over x}} + {1 \over \log^2{2}} \cdot {\log{x} \over \sqrt{x}} + {\log{x} \over \log^2{\sqrt{x}}}\\[2.0ex]
&= {{2 \over \log{2}} \cdot {\log{x} \over x}} + {1 \over \log^2{2}} \cdot {\log{x} \over \sqrt{x}} + {4 \over \log{x}}.\\[2.0ex]
\end{align}
The expression at the bottom goes to zero as \(x\) goes to infinity, so \(\text{Li}(x)/A(x) \rightarrow 1\) as \(x \rightarrow \infty\) and \( {\pi(x) \over \text{ Li}(x)} \rightarrow 1 \) if and only if \( {\pi(x) \over {x / \log{x}}} \rightarrow 1. \)QED.
| \(x\) | \(\pi(x)\) | \(\text{Li}(x)\) | \(x\over\log{x}\) | \(\pi(x)\over\text{Li}(x)\) | \({\pi(x)\over{x/\log{x}}}\) |
| 100 | 25 | 30.13 | 21.71 | 0.830 | 1.151 |
| 1000 | 168 | 177.61 | 144.76 | 0.946 | 1.161 |
| 10,000 | 1229 | 1246.14 | 1085.74 | 0.986 | 1.132 |
| 100,000 | 9592 | 9629.81 | 8685.89 | 0.996 | 1.104 |
| 1,000,000 | 78498 | 78627.54 | 72382.41 | 0.998 | 1.084 |
Although either \( \text{ Li}(x) \) or \( A(x) = x / \log{x} \) can be used to approximate \( \pi(x), \text{ Li}(x) \) does so much better, as this chart shows. In the bottom row, for example, \( \pi(x) \over \text{Li}(x) \) is 50 times closer to 1 than \( \pi(x) \over {x / \log{x}} \) is.
Mike Bertrand
November 28, 2020
^ 1. Essai Sur La Théorie Des Nombres, 2nd edition, by A. M. Legendre, Courcier (1808). See p. 394 for the formula and table.
^ 2. Carl Friedrich Gauss Werke, Band II. See p. 444 for the letter to Encke. His prime tables are at pp. 435-443.
^ 3. The entire letter is translated into English in "A History of the Prime Number Theorem", by L. J. Goldstein, The American Mathematical Monthly, Vol. 80, No. 6 (1973), pp. 599-615. This invaluable article considers Legendre's and Gauss's anticipation of the Prime Number Theorem, as well as subsequent work in the nineteenth century by Dirichlet, Chebyshev, and Riemann. The translation of the letter to Encke is in Appendix B, pp. 612-614.
^ 4. Goldstein, p. 603.
^ 5. This proof is in Goldstein, pp. 599-600.
