Gerbert's Abacus Illustrated

Gerbert's abacus with representative numbers

Gerbert of Aurillac was a Benedictine monk from this small village in south-central France who was born about 950 AD and died in 1003. He was a great teacher and scholar, politician and church leader. He became Pope Sylvester II in 999 and served in that role till his death. He was the first French pope and the only mathematician to become pope. And mathematician he was, sent as a young man by his abbot to study in Christian Spain, bordering Al-Andalus, then a shining light of Islamic civilization. The first documented appearance of the Hindu-Arabic numerals in Christian Europe was in 976 in a manuscript by Vigila, a monk in the vicinity of Barcelona, then a Christian outpost in northern Spain near where Gerbert resided from 967 to 970. Gerbert brought the Hindu-Arabic numerals he encountered in Spain back to Christian Europe for an abacus / counting board he invented which was subsequently named after him.

At that time, Europeans did have counting boards based on place value and powers of ten, but each column needed up to five counters to represent a digit, considering that each digit was represented by a five higher on the board, if needed, and up to four ones. The columns had to be reduced repeatedly in the course of calculations to reduce clutter. You're doing that anyway in the case of addition and subtraction, but multiplication was cumbersome with the necessity for the repeated reduction of subtotals — if this is confusing, walk through the animation below representing every digit with a five and ones. Undifferentiated counters of some kind (pebbles in days past, calculi in Latin!) were placed in each column and removed too as the calculation proceeded. Gerbert's great innovation was to mark these counters with the Hindu-Arabic numerals \( 1 \) to \( 9 \) in order to compactly represent one or more digits in each column. These counters were called apices (singular: apex) before and after Gerbert. There was no need for \( 0 \) in a column, all you had to do was leave the column blank when representing a number with no contribution from a given power of ten.

Rotate apices to make them look more like modern numerals

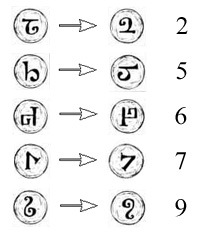
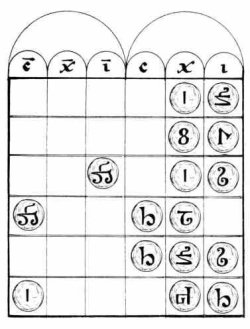
In the image of the abacus above, the columns represent powers of ten with the units on the right, the tens in the second column from the right, and so on, just as we do. Note the Roman numerals at the top of each column, \( \text{i}, \text{x}, \) and so on — \( \overline{\text{i}} \) stands for thousands, \( \overline{\text{x}} \) for ten thousands, \( \overline{\text{c}} \) for hundred thousands. Most of the digits don't look much like ours, though closer when rotated appropriately (and reflected in the case of the \( 7 \)). The apex at the upper right is a \( 3, \) barely recognizable, while the \( 4 \) in the thousands column is beyond recognition. The first four numbers represented are \( 13, 87, 4019, \) and \( 400,520, \) columns simply being empty where we would put a zero. The abacists of the day weren't necessarily readers, but were rather practitioners on this instrument. Their apices were in piles and oriented every which way on the table. The orientation might not have meant much to them or maybe different abacists preferred different orientations. Adding is easy if you know how to add two digits, carrying a \( 1 \) if necessary. Were the numbers on the abacus above to be added, for example, the \( 1 - 8 - 1 \) in the tens column can be removed and replaced by a single \( 1 \) in the hundreds column. The \( 1 \) counter is literally carried to the next column, presumably the origin of this term when talking about adding. The beauty of it is that such reductions can be done in any order.

Consider this multiplication problem, where each two-digit partial product is written on a separate row and trailing zeros are left out^[1]:
\begin{array}{cccc|c}
&3 &2 &5 & \leftarrow \text{multiplicand}\\
\times &&2 &8 & \leftarrow \text{multiplier}\\
\hline
&&4\\
&1 &6\\
2 &4\\
&1\\
&4\\
6\\
\hline
9 &1 &&& \leftarrow \text{final product}
\end{array}
Start from the right as usual, multiplying \( 8 \) by \( 5 \) to get \( 40 .\) We can dispense with the zero in the units column as long as we put the \( 4 \) in the tens column. Then multiply the \( 8 \) in the multiplier by the next digit in the multiplicand, \( 2, \) to get \( 16. \) Since one of the factors is in the tens column, the \( 16 \) has to be placed one column to the left. Put differently, multiply \( 8 \) by \( 20 \) to get \( 160, \) but leave the zero out. After the \( 8 \) has been multiplied by all the digits in the multiplicand, start multiplying the \( 2 \) in the multiplier by each digit in the multiplicand, starting from the right in the usual way. The key at each step is to put the partial products in the correct column, which depends in a simple way on the columns of the two digits being multiplied. Then add all the partial products, carrying as necessary, to get a final product of \( 9100, \) considering that the \( 91 \) is shifted two columns to the left. This would have to be converted to Roman numerals in order to be written down: \( 9100 = \overline{\text{IX}}\text{C}, \) using the convention that overlined numerals are in the thousands. This is exactly how Gerbert's abacus worked, except as a physical device with actual columns and the digits realized as apices, namely, little checker-like counters with digits on them. Walk through this calculation step-by-step by running the animation shown here.

It appears Gerbert's abacus was only used for two hundred years or so, till about 1200. That seems puzzling to a modern observer, even after discounting a Whiggish preference for our own numerals and methods. It seems incontestable that Gerbert improved number representation and algorithms compared to the old abacus, yet abacists reverted to an inferior ancient instrument. By 1300, manuscript abacus manuals had virtually disappeared, being replaced by manuals on "algorism", the approach we still use today^[2] exemplified by Fibonacci in his Liber Abbaci of 1202. The name notwithstanding, Liber Abbaci concerned the new approach to expressing numbers exclusively with Hindu-Arabic numerals with place value and zeroes and calculating on any surface along on-the-spot columns — I almost said paper-and-pencil calculations like are still use today, and while the second part is true, the first is figurative only, there being no pencils and precious little paper in Europe at that time.

While new to Europe, the Hindu-Arabic numerals, base-ten place value, and the standard algorithms for addition, subtraction, multiplication, and division were promulgated in the Islamic world hundreds of years earlier, in particular by al-Khwarizmi (b. ~780 AD). In fact, Latin translations of al-Khwarizmi were instrumental in bringing the subject to Europe. The term algorism used in Europe for centuries for this circle of ideas was a corruption of al-Khwarizmi's name (as is the term algorithm, the word algebra being derived from his work on that subject). Fibonacci had spent time as a boy in a commercial counting house in north Africa and had traveled widely in the Mediterranean and Islamic worlds — this is where he learned the craft from Arabs or those close to them. Fibonacci gets top billing today for a number of reasons, including the prescience and magisterial nature of Liber Abbaci, but he was just one of the writers on the subject and was influential only indirectly^[3]. He was certainly respected in Italy, where a robust Abbaco culture transmitted algorism through commercial schools (sometimes called abacus schools by our own corruption of language) starting in the thirteenth century. The Latin algorism manuals of Sacrobosco and Alexander de Villa Dei were much-copied and used in the universities, but arithmetical studies there were much less sustained than in the vernacular abacus schools of Italy, where modern mathematics germinated.

It's plain from the extended multiplication example above that Gerbert's abacus was a short step removed from the "paper-and-pencil" algorist techniques that took Europe by storm in the thirteenth century. Even zero could've been dispensed with as long as temporary columns were laid out on the drawing surface. The algorists did bring in zero, but otherwise adopted abacist methods — while dispensing with the instrument itself. In the words of Suzan Rose Benedict:

Gradually the algorism displaced the abacus, but in the process absorbed something of the methods superseded, so that often, in expression or even in manner of operating we are reminded of mechanical calculation^[4].

In short, Gerbert's abacus was a bridge to the improved numeration and calculation schemes introduced by the algorists in the thirteenth century (the same ones we use today!). Sophisticated abacists moved on to algorism, less sophisticated ones reverted to the old abacus expounded by Robert Recorde and others as late as the sixteenth century. Practitioners had generations to acclimate to the Hindu-Arabic numerals through Gerbert's abacus and indeed to the new algorithms. All they had to do was replace his abacus with a writing instrument and introduce zero in order to enforce column alignment on any surface.

Mike Bertrand

July 28, 2018

^ 1. The Universal History of Numbers: From Prehistory to the Invention of the Computer, by Georges Ifrah, Wiley (2000), ISBN 978-0471375685. I've followed Ifrah closely in the multiplication example (pp. 582 - 585), part of his invaluable Chapter 26, The Slow Progress of Indo-Arabic Numerals in Western Europe.

^ 2. "From Abacus to Algorism: Theory and Practice in Medieval Arithmetic", by Gillian R. Evans, British Journal for the History of Science 10, 2 (1977) pp. 114-131.

^ 3. Jens Høyrup has written convincingly on the limited impact of Fibonacci, respected though he was, and is. See "Leonardo Fibonacci and Abbaco Culture. A Proposal to Invert the Roles", by Jens Høyrup, Revue d'histoire des mathématiques, 10 (2005), pp. 23-56. Also "Fibonacci - Protagonist or Witness? Who Taught Catholic Christian Europe about Mediterranean Commercial Arithmetic?", by Jens Høyrup, Journal of Transcultural Medieval Studies, 1, 2 (2014), pp. 219-247. In the former, Høyrup says that Abbaco culture ("paper-and pencil" calculating) "must be traced to an environment that already existed in Fibonacci's days — an environment he knew about and of which he can be regarded an extraordinary early exponent, but no founding father." (p. 23)

^ 4. "A Comparative Study of the Early Treatises Introducing into Europe the Hindu Art of Reckoning", by Suzan Rose Benedict (dissertation, 1914). The quote is on p. 119.