Calendar
My original calendar program was on the Casio fx-3600p calculator in 1980 or so - my first programming venue and exercised partly in spare moments when driving truck out on the route; a precursor mobile device you could say. My buddy Dave got me started. I might have scarred myself permanently though. The transition from math to software engineering is always tricky, considering that there are many commonalities, but just as important differences to snag the self-taught and perhaps obstinate and all-too-confident mathematician (perish the thought). The 3600 had this bizarre little macro language providing for a trade-off between memory and program size. You could have (say) fifty memory locations and 400 instructions or twenty locations and 600 instructions. They're really variables of course, but the memory locations were designated K0 through K19 or something.
The idea of a macro language is that any instruction executable manually can be batched together with others in a stored program and executed in sequence; instructions like "Load 17 into memory location K12" or "Display the square root of memory location K3". Variables, loops, conditions, subroutines, it's all there and more than a little like assembly language. If I remember, branching depended on whether there was a certain value in a certain memory location. You could get a nifty little printer that printed electrostatically on special silver paper about an inch and a half wide and there was just enough room to print seven spaced two digit numbers across, sufficient for a calendar display in standard format. Loved those little calendars.
So drawing a calendar was one of my projects for students when I started teaching programming. First C, then Visual Basic, Java, PHP, and Android. A friend who took a number of classes from me, Gary, exclaimed at one point mid-semester, "Hey Mike, when are we going to do the calendar?". I told the class I only have three ideas, but they're good ones, so I'm not giving them up.
The nice thing about this project, pedagogically speaking, is that it requires no input, assuming it's the current month to be displayed. Plus it gets people started on the time libraries in whatever language it is - always important (business programmers joke that time programming is 20% of what they do, no matter the ostensible assignment). And everyone knows the output expected, being familiar with standard calendars since childhood.
Then you can have a second assignment to do a perpetual calendar; that involves the user inputting the month and the year (extra credit for input validation!). Here is my PHP perpetual calendar, number two at google.com for that search term as of today. Mod 7 arithmetic is required at a number of points; so yes, simple undergraduate math can have continuing value for working programmers (number theory in this case). Technically, the key is to find the day of the week the first of the month falls on. You would derive a number, 0 for Sunday, 1 for Monday, and so on, and that tells you what column to put the 1 in, then the rest follows. In earlier versions, I would track forward from January 1, 1582, which was a Friday (check the perpetual calendar if you don't believe it!) to find the day of the week January first of the given year falls on, then track through the months of that year to get to the first day of the month in question. Yeah, mod 7. Modern date libraries provide the first day in a line or two (Javascript, for example).
You have to know the rule for leap years - every four years except century years, which are not leap years, EXCEPT years a multiple of 400, which are. Those are the rules promulgated by Pope Gregory in 1582 to amend Julius Caesar's simpler rule of a leap year every four years. So the year 2000 was exceptional, a once-in-400-year occasion when a year that is a multiple of 100 is a leap year, the second one since 1582. In other words, there are 97 leap years every 400 year cycle. Normally a year has 52 weeks and one day, that's why New Years day advances through the week year after year (Monday then Tuesday then Wednesday, and so on). But leap years have an extra day, February 29, so you leap ahead another day, that's where that comes from.
The church had always been involved in the calendar because of the necessity to keep Easter at about the same time of year, when Jesus celebrated his last supper at that Passover seder. In fact, early Christians depended on Jewish scholars for their dates, synchronizing Easter with Passover. As the church grew and prospered in the Roman world and even became official under Emperor Constantine the Great, the situation became untenable. Constantine called the church to the First Council of Nicaea in 325 to rectify this and many other important matters, including the divinity of Jesus.
The Council used the inadequate Julian calendar, resulting in Easter slipping gradually into the winter because the years since 325 were slightly shorter than they should have been (Wikipedia has a good writeup on the Gregorian calendar). The Gregorian reform included skipping ten days in October 1582, exactly what you'd expect if you were off three days every four hundred years [(1582 - 325) / 400 * 3 = 9.43]. Pope Gregory's scientists were uncannily accurate; I remember a Scientific American article in 1982 (anniversary of the first cycle!) saying it was due to offsetting errors, because the science of the time was nowhere near capable of such precision. There was terrific resistance in some quarters to this innovation from the papist dogs. George Washington's birthday will vary, for example, depending on whether it is given old style or new style (his life spanned the adoption in the English-speaking world in 1752). Those change mongers the tsars never did get around to it; so the Bolshevik seizure of power in 1917 was the October Revolution or the November Revolution, depending.
I know the Pope is infallible and all, but how in God's name did they come up with 97 leap years every 400 years ( 97 / 400 = 0.2425) instead of one leap year every four years (1 / 4 = 0.25)? We're trying to reconcile the earth spinning on it's axis with rotating around the sun, how many circuits of the first kind it takes for one of the second. The answer is a constant of nature known as mean tropical year, whose current value is approximately 365.2421897 days - 365 days, 5 hours, 48 minutes, and 45 seconds. So there are two problems to solve, one experimental and one mathematical. First is calculating that constant, second is finding a fraction with a fairly small denominator to approximate it (at least if we want a regular calendar down the centuries with a reasonably small cycle). The best approach to the math part (and this is an entirely general solution when approximating any real number) is to expand using continued fractions - see The Theory of Numbers, 1955, by Burton W Jones, for example.
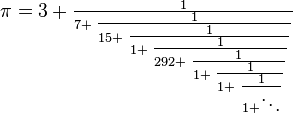 Here's the method as applied to π = 3.14159265359..., an irrational number whose expansion continues forever in an irregular fashion (graphic courtesy of Wikipedia). This is a problem of interest in its own right, since it provides usable approximations for this most most central of all mathematical constants. It is the fractional part after the decimal point we are interested in.
Here's the method as applied to π = 3.14159265359..., an irrational number whose expansion continues forever in an irregular fashion (graphic courtesy of Wikipedia). This is a problem of interest in its own right, since it provides usable approximations for this most most central of all mathematical constants. It is the fractional part after the decimal point we are interested in.
1 1 1
0.14159265359 = ----------------- = ----------- = ---------------
1 / 0.14159265359 7.062513305 7 + 0.062513305
See the 7 in the denominator on the right, just like in the image as the continued fraction starts to be expanded. Chopping off the decimal after the 7 (0.062513305) leads to the approximation π ~ 3 1/7 = 3.142857 used in grade school and no doubt by early forebears. The error is 0.0012645 (over). Then recurse, as we say in the computer business. Namely, do the same for 0.062513305, leading to:
1 1 15
0.14159265359 ~ -------- = -------- = --- = 0.141509434
7 + 1/15 106 / 15 106
This gives the approximation π ~ 3 15/106 = 3.141509, with error 0.000083 (under), 15 times better than before. One more time gets you π ~ 3 16/113 = 355 / 113 = 3.14159292, error 0.00000032, a 250-fold improvement. Correct to six places, that's good. Jones says the ancient Babylonians used that approximation and it wouldn't surprise me, knowing their bent for mathematics and astronomy. A more compact notation for the continued fraction representation of π is π = (3, 7, 15, 1, 292, ...). The canonical not-too-technical account of π, incidentally, is A History of Pi (1976) by Petr Beckmann, cranky old devil that he is and cheap now after all these years. Beckman says that in the late 19th century, the Indiana Assembly considered a bill declaring that the circle could be squared (impossible) and that π = 3.2. Amazingly enough, there is a thorough Wikipedia page on this sorry episode. Some things never change.
The fractions calculated above are the convergents of the continued fraction and they are the best possible approximations in this sense (Jones, p 89):
Theorem: If p / q is a convergent of the continued-fraction expansion for a real number x, there is no rational number a / b with b ≤ q which is closer to x.
Back to the calendar. For the mean tropical year, Pope Gregory's astronomers used 365.242546296 days - 365 days, 5 hours, 49 minutes, and 16 seconds, higher than the current value by 31 seconds. This was worked out in the thirteenth century using the the bizarre Ptolemaic system, circles within circles until your head hurts. Amazing. To quote Wikidedia (9/6/2013):
The Alfonsine Tables, published in 1252, were based on the theories of Ptolemy and were revised and updated after the original publication ... The length of the tropical year (using the equinox-based definition) was 365 solar days 5 hours 49 minutes 16 seconds. It was these tables that were used in the reform process that led to the Gregorian calendar. (The History of the Tropical Year, by Meeus & Savoie, 1992, p. 41)
If my calculations are correct, and I think they are because convergence is rapid, the continued-fraction expansion for the decimal part of the Alfonsine mean tropical year is 0.242546296 = (4, 8, 7, 2, 2 ...). The first five convergents are are as follows, the second to the last column the error relative to the value being approximated, the last column how many times better the error is relative to the previous one:
| x0 | 1 / 4 | 0.250000000 | +0.007453704 | |
| x1 | 8 / 33 | 0.242424242 | -0.000122054 | 61 |
| x2 | 57 / 235 | 0.242553191 | +0.000006895 | 18 |
| x3 | 122 / 503 | 0.242544731 | -0.000001565 | 4 |
| x4 | 301 / 1241 | 0.242546333 | +0.000000037 | 42 |
The error for the Gregorian calendar with 97 / 400 = 0.2425 is -0.000046296. Pope Gregory's astronomers could have gone with x1 = 8 / 33, which is only about three times worse than what they went with, 97 / 400. You'd need 8 leap years every 33 years, not so bad perhaps if you had leap years every four years for 28 years and then waited an extra year before the next leap year. x2 = 57 / 235 is almost seven times better than 97 / 400, but now the bookkeeping is getting a little ridiculous.
The best fraction approximation for a given denominator can be calculated like this. Say the denominator is 400. Multiply 0.242546296 by 400 to get 97.018. The product is closer to 97 than 98, so the best approximation with denominator 400 is 97 / 400. This little PHP program does the calculation for denominators up to 400 and outputs candidates with error less than 0.001. Here is an excerpt of the output - the first few, then only values with error < 0.000100:
den num error
------------------
33 8 -0.000122
37 9 +0.000697
62 15 -0.000611
70 17 +0.000311
91 22 -0.000788
95 23 -0.000441
103 25 +0.000172
107 26 +0.000444
115 28 +0.000932
120 29 -0.000880
128 31 -0.000359
.
.
.
169 41 +0.000057
202 49 +0.000028
235 57 +0.000007
268 65 -0.000009
301 73 -0.000021
305 74 +0.000077
334 81 -0.000031
367 89 -0.000039
371 90 +0.000041
400 97 -0.000046
This shows that 57 / 235 and the one immediately after, 65 / 268, are awfully good. But 97 / 400 is perfectly respectable and here's the point - they wanted a reasonable denominator base ten. Now you have a nice rule producing exceptions only every hundred years, the multiples of one hundred - easy to remember and the old rule abrogated only in those centennial years.
Certainly the calculations in this program would be relatively easy to do in the 16th century, if tedious. Another way to look at this is how many years it takes for the calendar you're using to drift from the real value by one day. The Gregorian reform of the Julian calendar amounts to correcting a drift of (1 / 4 - 97 / 400)-1 = (3 / 400)-1 = 400 / 3 = 133.33 years. Comparing the Gregorian fraction with the Alfonsine value for the mean tropical year leads to a drift of (0.242546296 - 97 / 400)-1 = 21,600 years, a measure of how close the Gregorian reformers were to the year length their astronomers gave them (pretty good!). Comparing the Gregorian fraction with the current value of the mean tropical year leads to a drift of (97 / 400 - 0.2421897)-1 = 3,223 years, much more pronounced, but only because the astronomers have got cracking in the last four hundred years.
This just scratches the surface. Much more can be found in the proceedings of a Vatican conference commemorating the four hundredth anniversary in 1982, titled Gregorian Reform of the Calendar, edited by Coyne, Hoskin, and Pedersen. Among other things, this amazing collection reveals that the inadequacy of the Julian calendar was well-known by the cognoscenti for some four hundred years before the Gregorian reform. The Alfonsine value for the drift is (1 / 4 - 0.242546296)-1 = 134.16 days - this was known in 1252! J. D. North in his article in the proceedings writes, "The general opinion prevailing in the sixteenth century was that J = 134 (J being the drift), although there were rival opinions". Also that "one of the most striking things about the late middle ages is that very few of the figures quoted in this connection originated in the Christian world itself, vigorous though astronomical activity was" (both quotes p 79). The sources of course were Islamic. The title of this article is The Western Calendar - Intolerabilis, Horribilus, et Derisibilis"; Four Centuries of Discontent, quoting from Roger Bacon in the thirteenth century, translation hardly needed::
[Kalendarium] est intolerabilis omni sapienti, et horribilis omni astronomo, et derisibilis ab omni computista.
Incidentally, Bacon flirted with a value of 130 for the drift all those years earlier, but finally settled on the inferior 125, though the latter has a rule similar to but even nicer than the Gregorian one, requiring 121 leap years every 500 years (1 / 125 = 4 / 500). The rule would be that centennial years are not leap years except for years a multiple of 500, which are.

The primary author of the Gregorian reform was Aloysius Lilius, acknowledged as the primus auctor even by other principals on Pope Gregory's calendar commission. There was a long period of consultation with Catholic rulers and scientists and a manuscript work of Lilius's was circulated widely; it was apparently not printed and as as of 1982, is lost. An epitome of the manuscript was printed - the Compendium Novae Rationis Restituendi Kalendarium - and that too was assumed lost until scholars turned up a number of copies in Italian libraries in the 1970s. The image at right is an extract; note the reference to Gregor. XIII Pont. Max. under the woodcut (Pontifex Maximus, the Supreme Pontiff). Also the doctissimis mathematicis (learned mathematicians) towards the bottom, to whom the work was sent. The illuminated woodcut shows Pope Gregory presiding over his calendar commission. All of this in the excellent article by G. Moyer about Lilius and the Compendium.
In the end the solid, memorable rule for leap years was probably wise and certainly prescient. People had been flirting with base ten for thousands of years, but it wasn't nailed down in Europe till exactly the time these scientists were working - Simon Stevin's breakthrough work on decimal fractions being published in 1585. Calendars have been intensely interesting to people for millenia for reasons practical and mystical. The Wikepedia article on the Gregorian calendar gives some idea of all the smart and industrious people who contributed to the project and as always, there are untold scientists and technologists toiling in the background who no one has ever heard of, including the mathematicians. And they got this one so very right, what a story.
Mike Bertrand
September 15, 2013

PS (02/04/2014): This adorable little kitty is on a recently unearthed calendar for the year 2000, the plastic is still on it. Drat, fourteen years too late. But wait, maybe that year will repeat itself, there will be another year with exactly the same calendar. It seems likely, in fact, considering that there are only fourteen calendars total. Specify the day of the week January first falls on and whether the year is a leap year and you have specified the calendar, you can write it down. Perpetual calendars in the past would have the fourteen different full-year calendars and then a key where each year was associated with it's calendar - 2000 is a type 5 year, and so on. Assuming an even distribution, we'd expect about 1 / 7 of leap years and 1 / 7 of non leap years to be of each type. Considering that leap years are approximately 1 / 4 of all years, that means that about 1 / 28 of leap years should be of a given type and 3 / 28 of non leap years.
We know from the online perpetual calendar that January 1, 2000 was a Saturday - no need to break the plastic on the actual calendar. It follows that January 1, 2004 was a Thursday, the calendar having advanced by five days, the fifth day because of the intervening February 29 in 2000 (check the online perpetual calendar!). In the same vein, January 1, 2008 will be a Tuesday. Because 5 and 7 are relatively prime, subsequent leap years will start on each possible day until coming back around to Saturday in 2028: Sat → Thu → Tue → Sun → Fri → Wed → Mon → Sat - advancing by five is the same as backing up by two, mod 7. In fact that will generally be the case except when centennial years throw off leap year calculations, confirming the rule of thumb above. By the same reasoning, 2056 and 2084 have the same calendar as 2000, but we can't go one more time to 2112, because 2100 is not a leap year. Bottom line - we have to wait another fourteen years before the calendar for 2000 recurs in 2028.
Here is a Javascript widget calculating calendar matches. Enter 2000 for the year to match and 2000 and 2200 for the range (the numbers showing by default in gray are hints, you have to actually type in the desired values). Then click the button to see years in that range with matching calendars. The matches shown are 2000, 2028, 2056, 2084, 2124, 2152, 2180. As mentioned, the 28 year period is interrupted around 2100, but then continues again starting at 2124.
The entire calendrical cycle repeats every 400 years, so we can find all years matching 2000 (mod 400) by matching 2000 in the range 2000 - 2399. There are 13 of them. In fact, there are 13, 14, or 15 for each pattern. This is as expected, since 400 / 28 = 14.29. You'd expect about three times as many matches in 400 years for a non leap year, and indeed matching the year 2001 over the range 2000 - 2399 returns 43 matches ((3 / 28) x 400 = 42.86).
It's that darn February that gums up the works - there are only seven patterns for January and indeed seven patterns for March 1 through December 31. So if we were willing to forget about January and February, we could break out the year 2000 calendar in 2017, because March 1, 2017 is a Wednesday, just as it is for 2000.
The Javascript for the calendar matching widget is here. Key logic calculating the day of the week January first falls on for a given year and whether it is a leap year is simply:
// First day of year (month 0, day 1). var d = new Date(yearToMatch, 0, 1); // Day of week for first day of year (0 = Sun, 1 = Mon, ..) var firstDay = d.getDay(); // Have leap year iff February has 29 days. isLeapYear = ((new Date(yearToMatch, 1, 29)).getMonth() == 1);
The first thing to notice is that Date objects in Javascript are valid over a vast range, certainly back to 1582, the start of the Gregorian period, and far into the future. It isn't at all obvious that this should be so, but it is. So a simple call to Date's getDay() method returns the key goods, the day of the week January first falls on. Then that zany one-liner to determine whether yearToMatch is a leap year. Date has a constructor taking (year, month, day), but the input will be interpreted within reason. Putting (2014, 5, 100), for example, creates the Date for June 100, 2014, the 100th day of June, making no sense ostensibly, but which Javascript interprets as the Date 99 days after June 1, 2014 - namely, September 8, 2014. So Date(yearToMatch, 1, 29) will always be valid and returns a Date object for February 29 or March 1 depending on whether it's a leap year or not; in the first case, the Date's month is February, in the second case March (note that 1 stands for February, 2 for March in Javascript's 0-based month designations). Tip of the hat to user2343063 at stackoverflow.
