Keep Away Game in HTML5 Canvas

Expand to entire article to play.

The Keep Away game was the last assignment in my Flash class and this is the port to HTML5 canvas, programmed in Javascript. Flash is declining for a number of reasons, including its proprietary nature and that it's not supported by the iPhone. Too bad, because Flash's ActionScript 3.0 is a thoroughgoing object oriented approach to graphics programming similar to Javascript. For the programmer, a circle or rectangle or any other figure suitable to be part of a display list is just an object with properties and methods. Many artists know Flash through the sophisticated Flash Pro environment, where they can create and store images efficiently with "symbols". Think Adobe Photoshop, apt in a couple ways considering that Adobe acquired Flash and developed ActionScript 3.0. Even animations are possible with "tweens". It's a nice in-between technology, where artists can experience Flash as as they always do, but be gently introduced to programming those objects in the code window. My approach is to forgo the environment entirely, except as a medium to execute ActionScript. The environment can be skipped entirely with Abobe's free compiler which turns ActionScript into .swf, which executes in the (free) Flash Player.

Here is the basic spec:

Write a Flash "Keep Away" game, with automatically moving "mines" patrolling the stage, bouncing off the sides. The player controls a "ship" with cursor keys, moving it up, down, left, or right in order to avoid the mines. The ship cannot escape the stage. The game ends when a mine collides with the ship.

The first step is to have circular mines patrolling continuously, bouncing off the walls. We can create a Mine class and use Javascript's setInterval() to have a callback function executed repeatedly every so many milliseconds. The latter is actually available in ActionScript 3.0, although there are a number of ways there to do this type of animation. Here's class Mine, depending in turn on class Point:

// class Point
function Point(px, py)
{
  this.px = px;
  this.py = py;
}

// class Mine
function Mine(p, radius, color, xSpeed, ySpeed)
{
  this.p = p;
  this.radius = radius;
  this.color  = color;
  this.xSpeed = xSpeed;
  this.ySpeed = ySpeed;
}

Mine.prototype.draw = function(ctx)
{
  ctx.beginPath();
  ctx.arc(this.p.px, this.p.py, this.radius, 0, 2 * Math.PI, false);
  ctx.fillStyle = this.color;
  ctx.fill();
  ctx.lineWidth = 1;
  ctx.strokeStyle = "black";
  ctx.stroke();
}

Mine.prototype.updatePosition = function()
{
  this.p.px += this.xSpeed;
  this.p.py += this.ySpeed;
}

Mine.prototype.reverseSpeedAtBoundary = function()
{
  var mineBottom = this.p.py + this.radius;
  // When hit bottom, ricochet at equal angles.
  if (mineBottom > canvas.height)
    this.ySpeed = -this.ySpeed;

  // Check other three sides similarly.
}

Function invalidate() below shows the basic logic for the repeatedly executing function. Considering that mines is a array of Mine objects, it simply draws the mines, then updates their positions and velocities as appropriate. Note the initial clearRect() to clear the canvas, so the old mines are erased before the new ones are drawn. A word on those velocities, which are handled in reverseSpeedAtBoundary() above. The condition shown senses when the mine hits the bottom of the canvas, then changes the sign of ySpeed, in essence reversing the velocity in the up-down direction; the net result is a bounce off the bottom at equal angles. The completed code has three more conditions to sense hitting the right, top, and left boundaries, with xSpeed or ySpeed updated as appropriate to produce bounces off those walls.

function invalidate()
{
  ctx.clearRect(0, 0, canvas.width, canvas.height);

  // Draw all mines, update as appropriate.
  for (var k = 0; k < mines.length; k++)
  {
    mines[k].draw(ctx);
    mines[k].updatePosition();
    mines[k].reverseSpeedAtBoundary();
  }
}

Next is the "ship"; that will be a five-pointed star and implemented in class Ship - much like class Mine, except with a different draw method. The five vertices are calculated with trig at object initialization in method generateVertices(), shown below. The method calculates the vertices of a regular polygon, in this case a pentagon, but simply change the value of NUM_SIDES on line 4 for a polygon of any size. The idea is to rotate a spoke around a circle at regular angular intervals, collecting the points along the circle into an array. The routine starts with a vertical spoke rising from the center to the top of the circle, then systematically rotates the spoke in a clockwise sense. To draw a star, connect every other vertex : 0 → 2 → 4 → 1 → 3.

Ship.prototype.generateVertices = function()
{
  var vertices = new Array();
  var NUM_SIDES = 5;
  
  // Calculate polygon's central angle in radians (72 deg for pentagon).
  var theta = (2 * Math.PI) / NUM_SIDES;
  
  // Get sine and cosine of central angle.
  var sinTheta = Math.sin(theta);
  var cosTheta = Math.cos(theta);
     
  // Initial vertex at top of circle; start rotating point there, store rounded copy.
  var rotPt = new Point(this.p.px, this.p.py - this.radius);
  vertices.push(new Point(Math.round(rotPt.px), Math.round(rotPt.py)));

  /* Go clockwise around circle calulating polygon points
   * (would be ccw in standard Cartesian system).
   */
  for (var side = 1; side < NUM_SIDES; side++)
  {
    // Calculate the radial spoke : rotPt - center (p).
    var spoke = new Point(rotPt.px - this.p.px, rotPt.py - this.p.py);
    
    // Generate new rotating point by rotating around center.
    rotPt.px = (spoke.px * cosTheta - spoke.py * sinTheta) + this.p.px;
    rotPt.py = (spoke.px * sinTheta + spoke.py * cosTheta) + this.p.py;
  
    // Store rounded copy of rotating point.
    vertices.push(new Point(Math.round(rotPt.px), Math.round(rotPt.py)));
  }
  
  return vertices;
}

This is something you don't have to do in Flash, incidentally, at least if willing to use the Flash environment to create such symbols with the polygon tool. Once created, switch to the code window and program those symbols.

The next task is to allow the user to move the ship around through the keyboard, done by adding an event listener like this:

document.addEventListener("keydown", keyDown);

The event listener is being added to the document, which presents some issues. For one, you might have to click the page initially to make sure it gets keystrokes. We're going to implement the four cursor keys for the user to move the ship in any on the four basic directions to escape colliding with a mine. There is a line of code to add when detecting cursor up or cursor down to make sure they are not passed to the page, resulting in its scrolling (the line is event.preventDefault(); - see the entire program for context). So scrolling up or down on this page with the cursor keys is disabled, something many users expect. A wrap-around effect is implemented, so when the ship goes off the canvas to the right under user control, it reappears at the far left; and similarly for all four directions. This is called the "torus universe", because it's as if those four edges were stitched together to form a torus, or donut.

Next is collision detection, or hit-testing - determining when the the ship collides with a mine. Geometrically, this occurs when the figures overlap. With these particular figures, collision occurs exactly when one of the vertices of the star is inside a circle constituting a mine (see postscript below).

In Flash's ActionScript 3.0, all these geometric figures would be objects in the strict sense - the mines, the ship, and circular play and pause buttons introduced for the user to control the game. And that is possible up to a point in Javascript, with both mines being instances of the Mine class, as mentioned above. For the buttons, you'd want a base class Button containing logic inherent to all Buttons, then have subclasses for each of the particular buttons with draw() functions specific to each subclass. The point is that a generic contains() function in base class Button could be called to determine if a point clicked by the user is in the button or not, implemented using the basic relation for a point \((x, y)\) to be inside a circle, namely \(x^2 + y^2 < r^2\) :

Button.prototype.contains = function(t)
{
  // t is a test point to check for being in the circle.
  var dx = t.px - this.p.px;
  var dy = t.py - this.p.py;
  return (dx * dx + dy * dy < this.radius * this.radius);
}

This is not possible in a direct way in Javascript; there are workarounds, but of a "more trouble than they're worth" variety. Javascript is based on ECMAScript like ActionScript 3.0, but this is one instance where the Adobe extensions are a real aid to the object oriented programmer, with decent inheritance (strong typing is another). Another superior feature of Actionscript 3.0 is hit-testing between objects - not particularly difficult in this game because of the specific geometry of the figures involved, but considerably more difficult for complex figures. Z-order is another thing built into ActionScript 3.0 (which objects are considered to be "on top" of other objects). We can just roll our own for simple exercises, like here: the mines pass over the buttons because they are rendered after the buttons. But more robust z-order handling becomes increasingly helpful in complex projects. And clickable buttons, implemented here from scratch but available as objects with event handlers in ActionScript 3.0.

Here is the entire game, 450+ lines, and it would be shorter and simpler in ActionScript 3.0. The score is based on the time spent actively dodging the mines, pause periods not included. Enhancements might include speeding up the mines or introducing additional ones at time milestones. Another would be posting scores by name to the server (possible in ActionScript 3.0 also with its Ajax-like facilities). I could see this as a one month project in class, were some of these extras required.

At one time or another I considered doing a game programming class. You'd have to decide the programming language; it could be HTML 5 canvas today, but Android would be good too. This would be one project. Another would be a solitaire-like card game. That was one of the projects in the Advanced Android class - four aces across the top and four "target rectangles" underneath them, each for a different ace, but in a different order. The task was to drag and drop each ace to its own target rectangle, the game done when all four have been successfully dropped. The screen shot shows an Android jigsaw puzzle app, Squares, where the user drags squares of different sizes onto the grid to completely fill the 32 x 33 rectangle if arranged right; the dragging engine is the same as for the card game. I had a word quiz project in the Android class as well, that's another possibility - no graphics, just standard Android views. That's half a class at least!

Mike Bertrand

January 5, 2014

^ PS: I'm assuming that the star (ship) overlaps a circle (mine) exactly when one of the star's vertices is inside the circle, but is that right? Consider this popup diagram, which shows that it's obviously true if the circle is much larger than the star, false if the circle is much smaller. We'd like to know the size of the circle right at the boundary, where the condition is true for larger circles, false for smaller ones. In order to develop the geometry, some familiarity with the regular pentagon is necessary. Start with this from the estimable Elbridge P. Vance (Modern Algebra and Trigonometry, Addison-Wesley, 1962 - now available from Amazon.com for 1¢ and well worth it all these years later). 36° and 72° are the critical angles and Vance shows that:

\[ \sin 36^{\circ} = {\sqrt{5 - \sqrt{5}} \over 8}, \hspace{30pt} \cos 36^{\circ} = {{\sqrt{5} + 1} \over 4} \]

Expressed in terms of the golden ratio, \(\phi = {{(\sqrt{5} + 1)} / 2} \approx 1.618\):

\[ \sin 36^{\circ} = {\sqrt{3 - \phi} \over 2}, \hspace{30pt} \cos 36^{\circ} = {\phi \over 2} \]

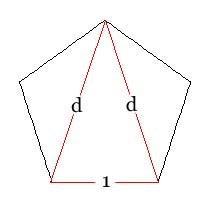
The diagram shows a regular pentagon with the red triangle being 36° - 72° - 72°, the two long sides being diagonals of the pentagon. Applying the law of cosines to that triangle:

\[ 1^2 = d^2 + d^2 - 2 \cdot d \cdot d \cdot \cos 36^{\circ} \]

\[ 1 = 2d^2 - 2d^2 \cdot \phi / 2 \]

\[ 1 = {2d^2(1 - \phi / 2)} = {d^2(2 - \phi)} \]

\[ \therefore d^2 = {1 / (2 - \phi)} = {1 + \phi} \]

The last step follows from the canonical relation \( \phi^2 - \phi - 1 = 0 \), as does the final step - \( d = \phi \). That is, the ratio of the diagonal to the side of a regular pentagon is \( \phi \).

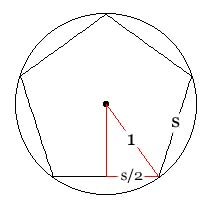
It will also help to know the ratio of the side of the pentagon to the radius of its circumscribing circle. For this calculation, consider the radius to be 1 and the length of the side s, as in the diagram. The top angle of the small triangle is 36°, so:

\[ \sin 36^{\circ} = {s / 2} \]

\[ \therefore s = {2 \cdot \sin 36^{\circ}} = {\sqrt{3 - \phi}} \approx 1.17557 \]

This is the ratio of the side to the radius of the enclosing circle.

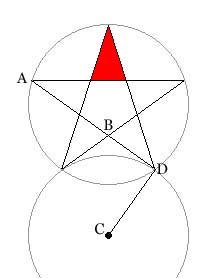
In the third diagram, a circular "mine" is below a star "ship". The star's vertices are those of a regular pentagon and in fact the star consists of pentagon diagonals and is drawn by connecting every other vertex of the pentagon. The configuration shown is the boundary situation mentioned above, where C is located directly below the pentagon's center and such that CD is perpendicular to AD. If C were any higher, \( \angle CDA \) would be less than 90° and the circle centered at C would overlap the star. Minute nudging would produce a circle overlapping the star but not including a star vertex. Likewise if C were any lower - \( \angle CDA \) would be greater than 90° and the lower circle would have no chance of overlapping the star without first enveloping one of its vertices.

So the task is to calculate CD. One more relation is needed, the ratio between the larger pentagon whose vertices are the same as the star and the smaller pentagon inside the star. Note this is the same as the ratio between the large 36° - 72° - 72° triangle whose longer sides are diagonals of the original pentagon and the smaller 36° - 72° - 72° triangles constituting the jutting points of the star, like the red one in the diagram. If that red triangle were flipped around its base, its vertex would coincide with B. In other words, the red triangle is congruent with the 36° - 72° - 72° triangle inside the smaller pentagon and its longer sides are the length of the smaller pentagon's diagonals. So we can analyse a longer diagonal like AD, which consists of three pieces - DB plus the two pieces BA is broken into. The smaller piece is the side of the smaller pentagon and the longer pieces (DB plus the other one) are the length of diagonals of that pentagon. But we know that the diagonal is \( \phi \) times the side, so the ratio of the two pentagons, which is the ratio of their diagonals (assuming the smaller pentagon has side 1) is:

\[ {{long \: diagonal} \over {short \: diagonal}} = {{\phi + 1 + \phi} \over \phi} = {{2\phi + 1} \over \phi} = {2 + {1 \over \phi}} = {2 + (\phi - 1)} = {\phi + 1} \]

Noting that \( \angle BCD \) in \( \triangle BCD \) is 36°, we have:

\[ {\tan 36^{\circ}} = {BD \over CD} \]

\[ \therefore CD = {{{\cos 36^{\circ}} \over {\sin 36^{\circ}}} \cdot BD} = {{\phi / 2} \over \sqrt{3 - \phi} / 2} \cdot {{long \: diagonal} \over {\phi + 1}} \]

The last step is because BD is a short diagonal, so a long diagonal is \( \phi + 1 \) times as long. Next we can maneuver that long diagonal to the side of the original pentagon and then the radius of the original circle using the relations developed above:

\[ CD = {{\phi \over \sqrt{3 - \phi}} \cdot {1 \over {\phi + 1}} \cdot ({\phi \cdot side})} =
{{\phi^2 \over \sqrt{3 - \phi}} \cdot {1 \over {\phi + 1}} \cdot ({\sqrt{3 - \phi} \cdot radius})} \]

This boils down to:

\[ CD = { {\phi^2 \over {\phi + 1} } \cdot radius } = radius \]

Voilà! The mine radius just the right size for simple hit-testing on the ship's vertices is exactly the radius of the circle circumscribing the ship.