Invariant Factor and Elementary Divisor Calculator
The Fundamental Theorem of Finite Abelian Groups decisively characterizes the Abelian finite groups of a given order. Its remote origins go back to Gauss in the Disquisitiones Arithmeticae in 1801 and it was nailed down by Schering (1869) and by Frobenius and Stickelberger (1879)[1]:
Fundamental Theorem of Finite Abelian Groups
Let \( G \) be a finite Abelian Group of order \( n. \) Then: \[ \begin{equation}{G \cong \mathbb{Z}_{n_1} \times \mathbb{Z}_{n_2} \times \cdots \times \mathbb{Z}_{n_s},} \tag{1} \end{equation} \] where \( s \) and the \( n_i \) are the unique integers satisfying \( s \geq 1, n_i \geq 2 \) for all \( i, \) and \( n_{i+1} \; | \; n_i \) for \( 1 \leq i \leq s - 1. \) And also: \[ \begin{equation}{G \cong \mathbb{Z}_{p^{\beta_1}} \times \cdots \times \mathbb{Z}_{p^{\beta_t}} \times \cdots \times \mathbb{Z}_{q^{\gamma_1}} \times \cdots \times \mathbb{Z}_{q^{\gamma_u}},} \tag{2} \end{equation} \] for \( p \) and \( q \) and all the other primes dividing \( n, \) again in a unique way, where \( \sum \beta_i \) is the exponent of the greatest power of \( p \) dividing \( n, \) \( \sum \gamma_i \) is the exponent of the greatest power of \( q \) dividing \( n, \) and so on for all the other primes dividing \( n. \)
The \( n_i \) in \( (1) \) are called the invariant factors of \( G \) and \( (1) \) is called the invariant factor decomposition of \( G. \) The \( p^{\beta_i}, q^{\gamma_i}, \) and all the other prime powers in \( (2) \) are called the elementary divisors of \( G \) and \( (2) \) is called the elementary divisor decomposition of \( G. \) To repeat, the invariant factors and elementary divisors for a given Abelian group are unique. Note that for a given \( n \) there are in general many ways \( \sum \beta_i, \sum \gamma_i, \) and the rest can be composed to equal the largest exponents of the primes dividing \( n, \) and there is a group for every combination. The key to finding all the Abelian groups of order \( n \) is finding all the ways this can be done for all the primes dividing \( n. \)
The Fundamental Theorem actually applies to all finitely generated Abelian groups, where a finite number of copies of \( \mathbb{Z} \) appear in the decompositions. That is the version appearing in §5.2 of Abstract Algebra (3d ed.), by David S. Dummit and Richard M. Foote. Dummit and Foote prove the theorem in a still broader context, finitely generated modules over a PID (§12.1), \( \mathbb{Z} \)-modules being synonymous with groups. Not only is the generalized version relatively easy to prove given some ring and module theory machinery, but it has unexpected (to me) applications to matrix canonical forms.
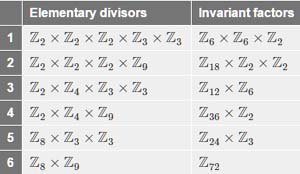
In order to find all Abelian groups of order \( n \), first express \( n \) in terms of its prime power representation. Let's work through \( n = 72 = {8 \cdot 9} = {2^3 \cdot 3^2}, \) as shown at the top of the page. First generate all integer partitions for the exponents in the prime power representation, \( 3 \) and \( 2 \) respectively. An integer partition of a positive integer is just a sum of integers adding up to the original value. So there are three partitions of \(3: 1 + 1 + 1, \color{red}{1 + 2} \) and \( 3. \) Likewise there are two partitions of \( 2: \color{red}{1 + 1} \) and \( 2. \) Using the notation \( p(n) = \) number of partitions of \( n, \) the foregoing says that \( p(3) = 3 \) and \( p(2) = 2. \) It's not always so simple of course — \( p(4) = 5, p(5) = 7, \) and \( p(6) = 11 \), for example. In fact, \( p \) grows exponentially, formulas appearing on the Wikipedia page just linked.
Associate each partition of \( 3 \) with each partition of \( 2 \) and build up a set of elementary divisors for each pair of partitions, then write down the elementary divisor decomposition for that pair of partitions. There are going to be \( p(2) \cdot p(3) = 2 \cdot 3 \) different Abelian groups of order \( 72. \) The red partition of \( 3 \) suggests elementary divisors \( 2^1, 2^2 = 4. \) Note that the exponent \( 3 \) is being partitioned, but the prime it is the exponent for is \( 2, \) hence \( 2^1 \) and \( 2^2 \) are the associated elementary divisors. The red partition of \( 2 \) suggests elementary divisors \( 3^1, 3^1, \) so this pair of partitions leads to the decomposition \( \mathbb{Z}_2 \times \mathbb{Z}_4 \times \mathbb{Z}_3 \times \mathbb{Z}_3, \) the third group listed at the top. Note that \( 2 \cdot 4 \cdot 3 \cdot 3 = 72, \) as must be the case.
Given the elementary divisors of an Abelian group, its invariant factors are easily calculated. Take \( G = {\mathbb{Z}_2 \times \mathbb{Z}_4 \times \mathbb{Z}_3 \times \mathbb{Z}_3} \) of order \( 72, \) just discussed. Write out all its elementary divisors, sub-grouping by each prime in the decomposition: \( \{ (2, 4), (3, 3) \} \). Remove the greatest number (the highest power of the associated prime) from each parenthesized subgroup. The product of all the extracted values is the first invariant factor, in this case \( n_1 = {4 \cdot 3} = 12. \) Repeat for the reduced list \( \{ (2), (3) \}, \) leading to the second invariant factor \( n_2 = {2 \cdot 3} = 6 \). The list is empty after extracting the \( 2 \) and \( 3 \), so the process is complete and the invariant factors for this group are \( n_1 = 12, \; n_2 = 6. \) Two invariant factors were calculated in this case before the list was exhausted, but in general, keep iterating until the list reduces to nothing.
Let's try one more, \( G = {\mathbb{Z}_{2}\times\mathbb{Z}_{2}\times\mathbb{Z}_{2}\times\mathbb{Z}_{3}\times\mathbb{Z}_{3}\times\mathbb{Z}_{25}}, \) a group of order \( 1800 \) given here in its elementary divisor decomposition. This time it takes two steps to reduce the list, leading to three invariant factors: \( \{ (2, 2, 2), (3, 3), (25) \} \rightarrow \{ (2, 2), (3) \} \rightarrow \{ (2) \}, \) leading to invariant factors \( {n_1 = {2 \cdot 3 \cdot 25} = 150}, \; {n_2 = {2 \cdot 3} = 6}, \; {n_3 = 2}. \) Enter \( 1800 \) in the calculator above to see that this group is one of those listed.
| \( g(n) \) | \( \#n \) with that \( g(n) \) |
|---|---|
| 1 | 607,926 |
| 2 | 200,780 |
| 3 | 74,182 |
| 4 | 22,126 |
| 5 | 32,072 |
| 6 | 14,497 |
| 7 | 14,744 |
For \( n \) a positive integer, let \( g(n) = \) number of Abelian groups of order \( n. \) \( g(n) \) can be calculated by looking at the partitions of the exponents of the prime power factorization of \( n, \) as discussed above. The chart shows low values of \( g(n) \) together with the number of values of \( n \) between \( 1 \) and \( 1,000,000 \) having that value for \( g(n). \; \) \( g(n) \) doesn't take all possible values by the way; there is no \( n \) such that \( g(n) = 13, \) for example (the lowest such). It's striking that over \( 60\% \) of values between \( 1 \) and \( 1,000,000 \) have \( g(n) = 1. \) These are exactly the values of \( n \) for which the exponents of their prime power factorization have a single partition; that is, their exponents are all \( 1. \)
Put another way, such an \( n \) is a product of different primes to the first power, a square-free integer. \( 17, \; 35 = 5 \cdot 7, \) and \( 30 = 2 \cdot 3 \cdot 5 \) are square-free, for example, while \( 12 = 2^2 \cdot 3 \) is not. Square-free values of \( n \) are exactly those having a single Abelian group of that order. If \( n = p \cdot q \cdots \), then \( \mathbb{Z}_n \cong \mathbb{Z}_p \times \mathbb{Z}_q \times \cdots \cong \mathbb{Z}_n, \) those being the elementary divisor and invariant factor decompositions respectively, and that is the only Abelian group of order \( n. \)
If \( Q(x) \) denotes the number of square-free integers between \( 1 \) and \( x, \) it turns out that:
\[ Q(x) = {{x \over \zeta(2)} + O(\sqrt{x})} = {{6x \over \pi^2} + O(\sqrt{x})}. \]
Plugging \( x = 1,000,000 \) into this formula without the error term results in \( Q(1,000,000) \approx \) \(607,927.102, \) just \( 1.102 \) over the calculated value! The Wikipedia page just linked has similar formulas for cube-free integers, and so on. The sum of the values in the right column of the chart is \( 966, 327, \) showing that for over \( 96\% \) of the integers \( n \) less than or equal to \( 1,000,000, \) there are \( 7 \) or fewer Abelian groups of order \( n. \)
On the other end, there are always \( n \) with as great a number of Abelian groups as desired — take \( n = 2^m \) for large \( m, \) for example. The four largest values of \( g(n) \) for the first million integers are as follows (put \( n \) into the calculator to see the corresponding groups!):
\[ g(n) = 490 = p(19) \;\; \text{for} \;\; n = 2^{19} = 524,288, \]
\[ g(n) = 505 = p(13) \cdot p(4) = 101 \cdot 5 \;\; \text{for} \;\; n = 2^{13} \cdot 3^4 = 663,552, \]
\[ g(n) = 528 = p(15) \cdot p(3) \;\; \text{for} \;\; n = 2^{15} \cdot 3^3 = 884,736, \]
\[ g(n) = 539 = p(12) \cdot p(5) \;\; \text{for} \;\; n = 2^{12} \cdot 3^5 = 995,328. \]
Mike Bertrand
June 9, 2016
^ 1. The Mathematics of Frobenius in Context: A Journey Through 18th to 20th Century Mathematics, by Thomas Hawkins (Springer, 2013), ISBN 978-1-4614-6332-0. A tour de force on Frobenius, an under-appreciated founder of the modern algebraic approach. See Chapter 9 for the Fundamental Theorem of Finite Abelian Groups.