Intersecting Chord Theorem for Ellipses

PG and DK are conjugate diameters and PG bisects chords QQ' and DK. Book 1, Proposition 21 of Apollonius's Conics implies that (PV×VG)/QV² = PC²/DC².

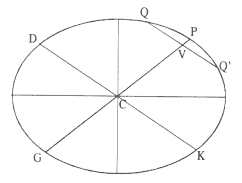
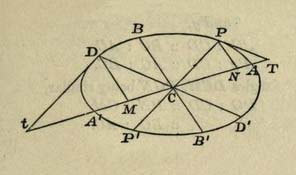
This image and caption are from J. Bruce Brackenridge's The Key to Newton's Dynamics: The Kepler Problem and the Principia^[1] (p 114). Newton used the result to prove that elliptical orbits imply an inverse square law. Note that PG and DK are "conjugate diameters" of the ellipse, meaning that PG is parallel to the tangent at D (or K - the tangents at D and K are themselves parallel). The situation is symmetric, so it is equally correct to say that DK is parallel to the tangent at P (or G). As the diagram suggests, all the chords parallel to one conjugate diameter are bisected by the paired congugate diameter. Conjugate diameters are an old concept going back at least to Apollonius; modern too since they map to perpendicular diameters of a circle through an affine transformation.

Brackenridge cites Apollonius, as Newton would have done were he in a giving frame of mind, but the old master is hard to understand. This preparatory theorem is Apollonius (I, 38) and here it is from a recently reissued 1890 work on conics by W. H. Besant^[2], (Article 73, Proposition XVII):

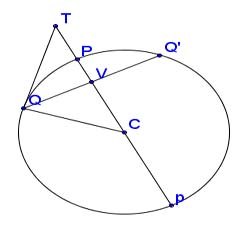
Besant: Proposition XVII

If PCp be a diameter [of an ellipse], and QVQ' a chord parallel to the tangent at P and meeting Pp in V, and if the tangent at Q meet pP produced in T, [then] CV·CT = CP².

Here is the picture and keep in mind that a diameter is simply a line segment through the center connecting opposite sides of the ellipse. Segment QQ' has a special relation to diameter PCp; namely, QQ' is parallel to the diameter conjugate to PCp. In older works, QQ' is called a double ordinate of diameter PCp - V bisects QQ', and QV and QV' are ordinates of the diameter. In circles, the ordinates are perpendicular to their diameters, but this is not true for the general ellipse.

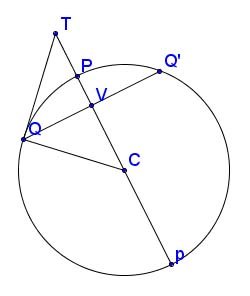
Besant has a rather forbidding diagram and discussion in proving Proposition XVII, including a series of construction points and lines. Let's look at the theorem for a circle and see if it's more tractable. The large triangle ΔCTQ is a right triangle because of the tangency at Q and the angles at V are also 90° because QQ' is parallel to the tangent at P. Those smaller triangles inside ΔCTQ are not 45°-45°-90°, but they are similar to each other and to ΔCTQ. That is because they have equal corresponding angles - ∠CQV in ΔCQV equal to ∠CTQ in ΔCTQ, for example. Therefore the sides of the two triangles just named are in proportion, and in particular:

\[ {CT \over CQ} = {CQ \over CV}. \]

But CQ = CP, because they are both radii of the circle, so:

\[ {CT \over CP} = {CP \over CV}. \]

Cross multiplying gives the result for circles. But how to prove it for ellipses?

An affine transformation of the plane (or affinity) is an invertible linear transformation followed by a translation; examples are scaling, shearing, and rotation. Affinities are pertinent here, because they take ellipses into ellipses and there is always an affinity taking an ellipse into a circle. Affinities preserve lines (lines map to lines) and parallel lines. Angles, perpendicularity, and lengths are not generally preserved, but ratios of lengths on the same line are. For a given affinity, areas are scaled by the same factor, so ratios of areas are preserved. The modern textbook Methods for Euclidean Geometry^[3] has a nice chapter on affinities.

The old timers' conjugate diameters tie into affinities nicely, because a pair of conjugate diameters maps to perpendicular diameters when an ellipse is mapped to a circle by an affinity. That's why a diameter bisects a chord parallel to it's paired conjugate diameter, because that's true in a circle mapped to the ellipse, and the affine mapping preserves bisection and parallel lines. The figures above show an ellipse scaled in y to produce the circle (that's how I created them in my graphics software - circle first, then scale to create the ellipse). Proposition XVII for ellipses falls out without even trying: scale the ellipse to a circle, prove the proposition for circles, then note that the ratios of interest are unchanged between the two figures, since they are along a single line.

Using the notation in this diagram, Apollonius (I, 21) says that for a given ellipse, \( QV^2 \propto PV \cdot Vp \); ie., \( QV^2 / (PV \cdot Vp) \) is constant. Sliding QV parallel to itself down to semi-diameter DC, and lengthening it so that Q corresponds to D and V to C, it follows that the constant is CD²/CP², as asserted below. This is the first chord theorem, Besant's Article 77, Proposition XX, and is Brackenridge's theorem at the top of this page with some relabeling:

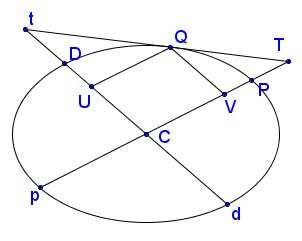
Besant: Proposition XX

If PCp, DCd be conjugate diameters [of an ellipse], and QV an ordinate of Pp, [then] QV² : PV · Vp :: CD² : CP².

I'll follow Besant's straightforward proof on this one. Draw the tangent at Q and extend pCP to meet the tangent at T; also extend dCD to meet the tangent at t. Draw the ordinate from Q to diameter DCd, meeting DCd at U (so \( QU \parallel PCp \) as well as \( QV \parallel DCd \)). Applying Proposition XVII twice, and noting that CU = QV, because they are opposite sides of a parallelogram:

\[ CP^2 = {CV \cdot CT}, \]

\[ CD^2 = {CU \cdot Ct} = {QV \cdot Ct}. \]

\[ \therefore {CD^2 \over CP^2} = {{QV \cdot Ct} \over {CV \cdot CT}} = {{QV \cdot QV} \over {CV \cdot VT}}, \]

the last step because \( \bigtriangleup CtT \sim \bigtriangleup VQT \) and so \( {Ct / CT} = {QV / VT} \). Expanding the denominator leads to:

\[ \small{{CV \cdot VT} = {CV \cdot (CT - CV)} = {CV \cdot CT - CV^2} = {CP^2 - CV^2} = {(CP - CV) \cdot (CP + CV)} = {VP \cdot Vp}.} \]

The only non-routine step in this chain is \( {CV \cdot CT} = CP^2\), which has already been used in this proof and follows from Proposition XVII. Substituting this for the denominator in the fraction above gives:

\[ {CD^2 \over CP^2} = {QV^2 \over {VP \cdot Vp}}, \]

which was to be proved, QED.

The second chord theorem, a generalization of the first, is stated this way in Heath's edition of Apollonius, which jumbles up Book III, Propositions 16-23:

The rectangles under the segments of intersecting chords in fixed directions are as the squares of the parallel semi-diameters.

It is Besant's Article 86, Proposition XXIX (see box at end of demonstration for an easier proof):

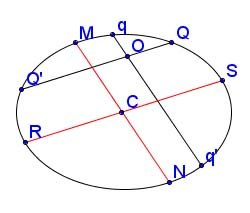
Besant: Proposition XXIX

The rectangles contained by the segments of any two chords [of an ellipse] which intersect each other are in the ratio of the squares of the parallel diameters.

The chords in question are QQ' and qq' in the diagram, meeting in O. RCS and MCN (in red) are diameters parallel to QQ' and qq' respectively. The theorem says:

\[ {{OQ \cdot OQ'} \over {Oq \cdot Oq'}} = {RCS^2 \over MCN^2} \hspace{10pt} \bigg( = {CS^2 \over CN^2} \bigg). \]

The part in parentheses is because it is equally valid to take diameters or half-diameters, the ratio is the same. Note that the two diameters in the diagram, in red, are not necessarily conjugate to each other, they are just parallel to the two chords respectively. We'll follow Besant.

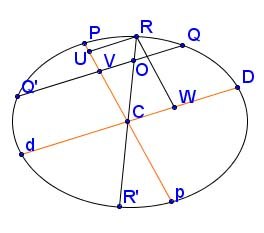
Start with just one of the chords, QQ', and draw diameter ROR' through point O on it. Let DCd be the diameter parallel to QQ' and PCp conjugate to DCd, bisecting QQ' at V. Drop the ordinate from R to point U on PCp, so \( RU \parallel QQ' \parallel DCd \). Also drop the ordinate from R to point W on DCd, so \( RW \parallel PCp \). The diagram here shows the construction, with the orange lines being conjugate diameters.

By Proposition XX:

\[ {{dW \cdot WD} \over RW^2} = {CD^2 \over CP^2}. \]

Because of the parallelogram in the figure, RW = CU and the factors in the numerator expand as:

\[ {dW = {dC + CW} = {dC + RU} = {CD + RU}}, \hspace{16pt} {WD = {CD - CW} = {CD - RU}}, \]

so plugging into the fraction gives:

\[ \begin{equation}{{{dW \cdot WD} \over RW^2} = {{{(CD + RU)} \cdot {(CD - RU)}} \over CU^2} = {{CD^2 - RU^2} \over CU^2}= {CD^2 \over CP^2}.} \tag{1} \end{equation} \]

The last two expressions being equated illustrate an alternative phrasing for Proposition XX, which involves running an ordinate down form a point on the ellipse like here from R to U. Substituting Q for R and V for U yields a similar equation:

\[ \begin{equation}{{{CD^2 - QV^2} \over CV^2}= {CD^2 \over CP^2}.} \tag{2} \end{equation} \]

Also:

\[ \begin{equation}{{RU \over CU} = {OV \over CV}, \hspace{10pt} {RU^2 \over CU^2} = {OV^2 \over CV^2},} \tag{3} \end{equation} \]

the first one because of similar triangles. Putting these together:

\[ {{{CD^2 - QV^2} \over CV^2} + {OV^2 \over CV^2}} = {{CD^2 \over CP^2} + {OV^2 \over CV^2}} = {{CD^2 \over CP^2} + {RU^2 \over CU^2}} = {{{CD^2 -RU^2} \over CU^2} + {RU^2 \over CU^2}} = {CD^2 \over CU^2}. \]

The first equality is by (2), the second by (3), and the third by (1). Connecting the first expression in this chain with the last one and rearranging:

\[ {CV^2 \over CU^2} = {{CD^2 + OV^2 - QV^2} \over CD^2}, \]

which, considering that CV / CU = CO / CR by similar triangles, can be written as:

\[ {CO^2 \over CR^2} = {{CD^2 + OV^2 - QV^2} \over CD^2}. \]

Subtract 1 from each side and change the sign to get:

\[ {{CR^2 - CO^2} \over CR^2} = {{QV^2 - OV^2} \over CD^2}. \]

Then factor the numerators:

\[ \begin{equation}{{{{(CR + CO)} \cdot {(CR - CO)}} \over CR^2} = {{{(QV + OV)} \cdot {(QV - OV)}} \over CD^2}.} \tag{4} \end{equation} \]

But:

\[ {CR + CO} = OR', \hspace{8pt} {CR - CO} = OR', \hspace{8pt} {QV + OV} = OQ', \hspace{8pt} {QV - OV} = OQ. \]

Plugging these four into (4):

\[ \begin{equation}{{{OR' \cdot OR} \over CR^2} = {{OQ' \cdot OQ} \over CD^2}.} \tag{5} \end{equation} \]

Just about done. Consider any other chord through O, meeting the ellipse at q and q'. Treating this chord just like the last one leads to:

\[ \begin{equation}{{{OR' \cdot OR} \over CR^2} = {{Oq' \cdot Oq} \over Cd^2},} \tag{6} \end{equation} \]

where Cd is the second chord's semi-diameter. Equating the right sides of (5) and (6) results in:

\[ {{OQ' \cdot OQ} \over {Oq' \cdot Oq}} = {CD^2 \over Cd^2}, \]

which was to be proved, QED.

A couple points about this theorem. First is that O can be outside the ellipse and the proof is the same - Besant's figure actually shows it that way. Second is that since CD and Cd are simply semi-diameters in the directions of the two chords, the chord's directions determine the ratio \( {{OQ' \cdot OQ}} : {{Oq' \cdot Oq}} \).

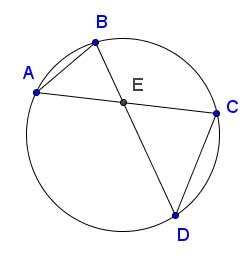
The chord theorem for circles falls out of Proposition XXIX for ellipses:

\[ {AE \cdot EC} = {BE \cdot ED}. \]

There is a two-line proof using similar triangles. It seems like you should be able to go from the circle to the ellipse with an affinity like the first theorem above, but I don't see it. The chord theorem for circles is Euclid III, 35, and he uses a more involved approach relying on the Pythagorean Theorem (Euclid I, 47). Triangle similarity is not elementary in Euclid's development and is not taken up until Book VI - see this helpful discussion.

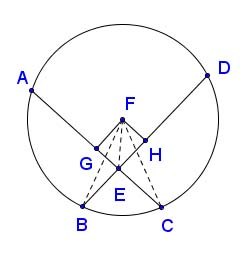
Here is Euclid's proof. Let AC and BD be the two chords meeting at E. Let F be the center of the circle and assume E ≠ F, otherwise the proof is trivial because each chord segment is a radius. Drop the perpendicular from F to chord AC, meeting AC at G; also drop the perpendicular from F to chord BD, meeting BD at H. Connect F to B, E and C.In such a construction, AG = GC because the perpendicular to a chord from the center bisects it. Therefore:

\[ AE = {AG + GE} = {GC + EG}. \]

Considering that GC - EG = EC:

\[ {AE \cdot EC} = {(GC + EG) (GC - EG)}. \]

Multiplying out and rearranging:

\[ {AE \cdot EC + EG^2} = GC^2. \]

Add GF² to both sides:

\[ {AE \cdot EC + (EG^2 + GF^2)} = {GC^2 + GF^2}. \]

Pythagoras says that EG² + GF² = EF² and GC² + GF² = FC², so:

\[ {AE \cdot EC + EF^2} = FC^2. \]

Exactly the same argument on the other chord establishes that:

\[ {DE \cdot EB + EF^2} = FB^2. \]

FC and FB are each radii of the circle, so equal. It follows that;

\[ {AE \cdot EC} = {FC^2 - EF^2} = {FB^2 - EF^2} = {DE \cdot EB}, \]

which was to be proved, QED.

There are a few more canonical theorems amenable to proof with these techniques and we might need them for the Newton work.

Theorem 1: In a given ellipse, the sum of the squares of conjugate half-diameters equals a² + b², where a and b are the major and minor axes respectively.

Of course a and b are themselves conjugate half-diameters. Theorem 1 is Apollonius VII, 12 and Besant Article 79, Proposition XXII. The diagram and proof here are from Besant, Article 78, Proposition XXI. Let ACA' and BCB' be a pair of conjugate diameters, PCP' and DCD' another pair, and PN, DM be ordinates of ACA' (meaning they connect points on the ellipse to ACA' along lines parallel to the conjugate of ACA' - BCB' in this case). Let the tangents at P and D meet ACA' at T and t. First show:

\[ \begin{equation}{{CN^2 + CM^2} = AC^2.} \tag{7} \end{equation} \]

By Besant, XVII above, applied twice:

\[ {CN \cdot CT} = AC^2 = {CM \cdot Ct}. \]

This leads to the following, relying on all the parallelism and the fact that \( \bigtriangleup tDC \sim \bigtriangleup CPT \):

\[ {CM \over CN} = {CT \over Ct} = {PT \over CD} = {PN \over DM} = {CN \over Mt}. \]

\[ \therefore CN^2 = {CM \cdot Mt} = {AC^2 - CM^2}. \]

The first equality is obtained by cross multiplying; the second mirrors the long series of equalities in the proof of Proposition XX above. This proves (7). Analogously, if Pn and Dm are ordinates of BCB':

\[ {Cn^2 + Cm^2} = BC^2. \]

\[ \begin{equation}{\therefore {PN^2 + DM^2} = BC^2,} \tag{8} \end{equation} \]

the second line because Cn = PN and Cm = DM, being opposite sides of parallelograms. If AC = a and BC = b are the principal semi-diameters (ie., the axes), ΔACB is a right triangle, so:

\[ \begin{equation}{{PN^2 + CN^2} = CP^2, \hspace{20pt} {DM^2 + CM^2} = CD^2.} \tag{9} \end{equation} \]

Adding (7) and (8) and substituting from (9):

\[ {CP^2 + CD^2} = {AC^2 + BC^2} ={a^2 + b^2}, \]

which was to be proved, QED.

Here is another well-known theorem from Apollonius (VII, 31). Besant includes it as Article 81, Proposition XXIV:

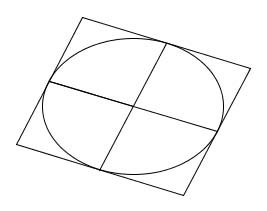
Theorem 2: In a given ellipse, the area of the circumscribing parallelogram touching the ellipse at the ends of conjugate diameters equals 4ab, where a and b are the major and minor axes respectively.

Newton needs this theorem and gives it as Lemma 12 of the Principia, noting that "this is demonstrated by the writers on the conic sections". He puts it like this:

Lemma XII: All parallelograms circumscribed about any conjugate diameters of a given ellipsis or hyperbola are equal among themselves.

The affine approach is productive here. The affinity mapping the ellipse to a circle maps the parallelogram to a circumscribing square, and all such parallelograms are mapped to circumscribing squares. All these squares are congruent and have the same area and since an affinity preserves the ratio of areas, all the parallelograms circumscribing the ellipse have the same area. The one that is a rectangle whose sides are parallel to the axes has area 4ab, so they all do. That's all there is to the proof!

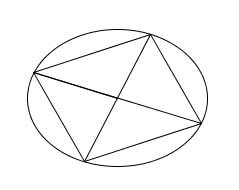
In the same vein as Theorem 2:

Theorem 3: In a given ellipse, the area of the inscribed parallelogram connecting the intersections of conjugate diameters equals 2ab, where a and b are he major and minor axes respectively.

The proof is similar to that for Theorem 2. In this case the parallelogram maps to a square inscribed in a circle. A square inscribed in a circle is half the area of a circumscribed square, which carries over to the ellipse - the inscribed parallelogram has half the area of the circumscribed one. Another approach is to draw diagonals on the four smaller parallelograms in the figure in Theorem 2, diagonals roughly in the same direction as the ellipse arc connecting the diagonal endpoints. Each of the little parallelograms is broken into two congruent triangles; simply removing the outer triangles results in the figure for Theorem 3. QED.

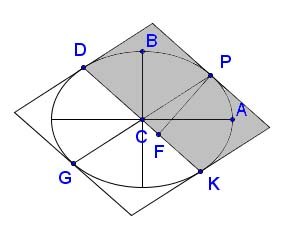
Newton needs this one in Proposition X, Problem V of the Principia:

Theorem 4: In a given ellipse, let PG and DK be conjugate diameters, AC = ½a and BC = ½b the semi-major and semi-minor axes of the ellipse respectively, and P any point on the ellipse. Drop the perpendicular from P to DK, meeting DK at F. Then CD·PF = ¼ab = CA·CB = constant.

The gray parallelogram has base DK and height PF, so by Theorem 2:

\[ {CD \cdot PF} = {1/2 \cdot DK \cdot PF} = {1/2 \cdot \text{Area(gray fig.)}} = {1/4 \cdot \text{Area(whole fig.)}} = {1/4 \cdot ab} = {CA \cdot CB}, \]

which was to be proved, QED.

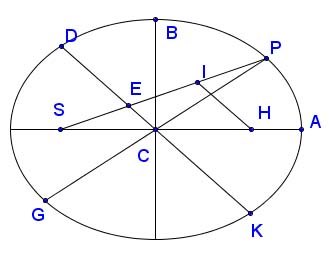
Here is another theorem Newton requires:

Theorem 5: In a given ellipse, let PG and DK be conjugate diameters, AC and BC the semi-major and semi-minor axes respectively, and S a fous, where PS crosses the minor axis and DK as pictured. Let E be the intersection of DK and PS. Then EP = AC.

Theorem 5 is used in Proposition XI, Problem VI of the Principia, arguably its most important, where Newton proves that elliptical orbits imply an inverse square law of attraction. He says "it is evident", but indulges us with a short proof as part of the proposition, as fleshed out here, again with Brackenridge's help. Note that:

\[ EP = {EI + PI} = {ES + PI}, \]

the second equality because EI = ES. That is because ΔSEC ~ ΔSIH due to EC being parallel to IH. Similar triangles and the smaller one is half as large as the bigger one because points S and H are situated symmetrically around ellipse center C, being foci.

\[ \therefore 2EP = {(ES + EP) + PI} = {PS + PI}. \]

But:

\[ {PS + PI} = {PS + PH} = 2AC. \]

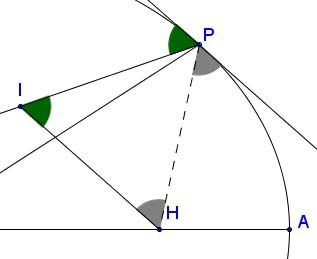
The second equality is because of the (sometimes defining) property of an ellipse that the sum of the distances from a point on the ellipse to the two foci is constant and equals the length of the major axis, 2AC. The first equality is because PI = PH. Consider the zoomed-in part of the diagram here to see why. The green angles are equal because they are alternate interior angles of a traversal cutting parallel lines. Ditto the gray angles. But the two colored angles at P are themselves equal because of the focal reflecting property of ellipses: the angle of incidence equals the angle of reflection for line segments connecting the foci to a point on the ellipse (that fact we still learn in high school today). So the colored angles at I and H are equal, ΔPIH is isosceles, and PI = PH as claimed. Therefore 2EP = 2AC, and so EP = AC, which was to be proved, QED.

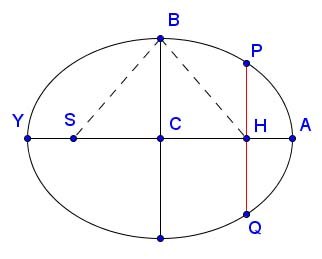
And finally a theorem concerning an ellipse's latus rectum, also used in Proposition XI, Problem VI of the Principia. An ellipse's latus rectum is a double ordinate of the major axis going through a focus, shown here in red - that is, a chord through a focus perpendicular to the major axis (a given ellipse has two of them).

Theorem 6: If a = AC and b = BC are the major and minor axes of an ellipse, respectively, then the length of the latus rectum is given by:

L = 2 · b ² / a = 2 · BC ² / AC.

Referring to the diagram, the first chord theorem proven above says:

\[ \begin{equation}{{{AH \cdot HY} \over PH^2} = {AC^2 \over BC^2}.} \tag{10} \end{equation} \]

For a circle, the right side is radius² / radius² = 1, which follows from the chord theorem for circles. The formula implies that the point H and the vertical chord through it can run along the ellipse's major axis and the expression on the left is constant for the ellipse. From the focal property of ellipses:

\[ {BH + BS} = 2AC \]

\[ \therefore 2BH = 2AC , \hspace{15pt} \text{so} \hspace{5pt} BH = AC. \]

Pythagoras says:

\[ {BC^2 + CH^2} = BH^2 = AC^2. \]

\[ \therefore BC^2 = {AC^2 - CH^2} = {(AC - CH)(AC + CH)} = {AH(AC + CS)} = {AH \cdot AS} = {AH \cdot HY}. \]

Substituting BC² = AH · HY into (10):

\[ {BC^2 \over PH^2} = {AC^2 \over BC^2}, \hspace{15pt} \text{or} \hspace{5pt} {BC \over PH} = {AC \over BC}. \]

Therefore if L is the length of the latus rectum:

\[ L = 2 \cdot PH = 2 \cdot {BC^2 \over AC}, \]

which was to be proved, QED.

Mike Bertrand

August 9, 2014

---

^ 1. The Key to Newton's Dynamics: The Kepler Problem and the Principia, by J. Bruce Brackenridge, University of California Press (1995), ISBN 0-520-20217-1.

^ 2. Conic Sections, Treated Geometrically, by W. H. Besant, HardPress Publishing (2013), ISBN 978-1314604559 (originally published 1890).

^ 3. Methods for Euclidean Geometry, by Owen Byer, Felix Lazebnik and Deirdre L. Smeltzer, Mathematical Association of America (2010), ISBN 978-0883857632.