Eratosthenes Measures the Earth

Eratosthenes Measures the Earth

Like Aristotle^[1] before him and in keeping with virtually all educated opinion in ancient Greece^[2], Eratosthenes (c. 276 BC - c. 194 BC) assumed the earth was spherical. He set out to measure its size using a sound method that has stood the test of time. His results were good (about \( 5.4\% \) too high) and no one did better for over a thousand years. His near correct result was ignored well into the modern era, including by Columbus. Snellius and Picard finally nailed down the earth's circumference in the seventeenth century using Eratosthenes' experimental design and taking advantage of advances in mathematics and instrumentation that had accrued over the intervening \( 1900 \) years.

Like so many ancient works, virtually nothing remains of Eratosthenes' The Measurement of the World^[3]. What a tragedy, and not just for the antiquarian, considering how much good thought they often contained (Aristarchus of Samos, a contemporary of Eratosthenes, posited a heliocentric theory some 1800 years before Copernicus, for example). The first extant reference to Eratosthenes' earth-measuring appeared in a handbook of the Stoic Cleomedes, The Heavens, recently published in a heavily annotated English translation by Alan Bowen and Robert Todd^[4]. According to these leading experts, The Heavens was likely written in the late second century AD, conceivably as early as 50 AD, almost certainly not much after 200 AD (Bowen and Todd, pp. 2-4) — 300+ years after Eratosthenes. Such handbooks were common in that day and for years to come in Christian Europe — diluted, confused, and plagiarized but sometimes extensive third-hand accounts for educated but non-expert readers as a barren dark age descended.^[5]. Much like Christians of later ages, Stoics were interested in celestial phenomena as evidence for their world-view. It's as if historians far in the future had only a tendentious freshman-level Physics for Poets textbook used by home-schoolers to learn about present-day understanding of nuclear physics. No one would care about Cleomedes if there were anything better, but there isn't, so thank the gods for this early and reasonably competent handbook. But read Cleomedes for yourself, as translated by Bowen and Todd (pp. 81-84)::

Eratosthenes' calculation, by contrast, involves a geodesic procedure, and is considered to possess a greater degree of obscurity. But the following assumptions, when stated by us as presuppositions, will clarify his account.

Let us first assume here too that Syene and Alexandria are located below the same meridian; second that the distance between the two cities is 5,000 stades. Third, assume that the rays sent down from different parts of the Sun to different parts of the Earth are parallel, as geometers assume to be the case. Fourth, let the following assumption demonstrated by geometers be made: that straight lines intersecting with parallel lines make the alternate angles equal. Fifth, assume that the arcs of circles standing on equal angles are similar, that is, have the same proportion (namely, the same ratio) to their own circles, as is also demonstrated by geometers. (For example, when arcs stand on equal angles, then if one of them is one-tenth part of its own circle, all the remaining arcs will also be one-tenth parts of their own circles.)

Someone who has mastered these assumptions would have no difficulty in learning Eratosthenes' procedure, which is as follows. He says that Syene and Alexandria are located below the sane meridian. So since the meridians are included among the great circles in the cosmos, the circles of the Earth located below them are necessarily also great circles. Thus the size that this procedure demonstrates for the arc of the circle of the Earth through Syene and Alexandria will be in a ratio with the great circle of the Earth.

Eratosthenes says, and it is the case, that Syene is located below the summer tropical circle. So when the Sun, as it enters Cancer and produces the summer solstice, is precisely at this meridian, the pointers on the sundials are necessarily shadowless, since the Sun is located vertically above them. (This shadowless area is reportedly 300 states in diameter.) But in Alexandria at the same hour pointers on sundials do cast a shadow, since this city is located further north than Syene. Now since the two cities are located below a meridian (a great circle), if we draw an arc from the tip of the pointer's shadow on the sundial at Alexandria round to the base of the pointer, this arc will be a section of the great circle in the sundial's bowl, since the sundial's bowl is located beneath a great circle.

If we next conceive of straight lines produced through the Earth from each of the pointers, they will coincide at the center of the Earth. So since the sundial at Syene is located directly below the Sun, then if we also conceive of a straight line going from the Sun to the tip of the sundial's pointer, the line going from the Sun to the center of the Earth will be a single straight line. If we conceive of a second straight line drawn from the bowl at Alexandria, that is, from the tip of the pointer's shadow up to the Sun, this line and the first one will be parallel, since they extend from different parts of the Sun to different parts of the Earth.

Now a third straight line extending from the center of the Earth to the pointer at Alexandria meets these parallel lines, and as a consequence makes the alternate angles equal. One of these angles is at the center of the Earth where the lines drawn from the sundials to the center of the Earth coincide. The other is where the tip of the pointer at Alexandria and the line drawn from the tip of the pointer's shadow up to the Sun through the point where the line touches the tip coincide. The arc drawn from the tip of that pointer's shadow round to its base stands on this second angle, while the arc extending from Syene to Alexandria stands on the angle at the center of the Earth.

Now the arcs are similar to one another, since they stand on angles that are equal. Thus the ratio that the arc in the bowl at Alexandria has to its own circle is the same as the ratio of the arc from Syene to Alexandria to its own circle. The arc in the bowl is certainly determined as one-fiftieth part of its own circle. So the distance from Syene to Alexandria is necessarily one-fiftieth part of the great circle of the Earth: namely 5,000 stades. Therefore, the great circle of the Earth totals 250,000 stades. And that is Eratosthenes' procedure.

Also, at winter solstices sundials are positioned in each of these cities, and when each sundial casts shadows, the shadow at Alexandria is necessarily determined as the longer because this city is at a greater distance from the winter tropic. So by taking the amount by which the shadow at Syene is exceeded by that at Alexandria, they also determine this amount as one-fiftieth part of the great circle in the sundial. So it is evident from this calculation too that the great circle of the Earth is 250,000 stades. Thus the diameter of the Earth will exceed 80,000 stades, given that it must certainly be 1/3 of the great circles of the Earth.

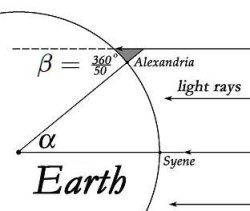
Noting that the sun was directly overhead at noon in Syene (modern day Aswan) on the summer solstice, Eratosthenes measured the shadow cast by a vertical stick in Alexandria at noon that same day. Assuming that the sun's rays at the two locations are parallel and given the distance between Syene and Aswan, simple geometry involving similarity led to an estimate of the earth's diameter. He assumed the distance between Syene and Alexandria was 5000 stades, the stadion being a unit of distance in those days. Presumably the distance was provided by the surveyors of the Egyptian ruler of the day. As suggested by the figure at the top, he measured angle \( \beta \) as \( 1 / 50 \)^th of a circle. By alternate interior angles, that would also equal angle \( \alpha \), the angle between Syene and Alexandria from the center of the earth. Therefore \( \alpha \) is \( 1 / 50 \)^th of its big circle around the earth, that is, the earth's circumference. It follows that the the earth's circumference is \( 50 \times 5000 \) stades = \( 250,000 \) stades.

The science here is absolutely solid and elegantly simple. Cleomedes' fifth item, that arcs over equal angles are similar, is so fundamental that it is a definition in Euclid (Euclid III, definition 11). His fourth item, that a transversal to parallel lines has equal alternate interior angles, is a staple from Book I of Euclid, and has been for 2300 years (Euclid I, 29). That is the required geometry, all of it. That there is a shadow at Alexandria itself provides good evidence that the surface of the earth is curved.

There are a number of empirical issues affecting the experiment's outcome. Cleomedes' first assumption is that Syene and Alexandria lie on the same meridian, that is, that Alexandria is directly north of Syene, that they have the same longitude. This is not the case or even terribly close (Alexandria \( 29^{\circ} 55' \text{ E} \), Aswan \( 32^{\circ} 54' \text{ E} \) ). But the point is irrelevant, since the experiment will measure the great circle connecting Syene and Aswan, whether a meridian or not.

The closeness of Syene to the "summer tropic" is more to the point — that's the Tropic of Cancer at \( 23^{\circ} 26' 13.3'' \text{ N} \), the most northerly circle of latitude on the earth at which the sun can be directly overhead. In fact, Syene / Aswan is at \( 24^{\circ} 05' 20'' \text{ N} \), and Eratosthenes would have been hard pressed to detect that difference. Cleomedes himself notes that the shadowless belt extends over three hundred stades. Syene is close to the tropic though, the exact location where the sun is directly overhead at noon on the summer solstice, the day experimenters far to the north could check the shadow.

Cleomedes' third assumption, that the rays of the sun all strike the earth in parallel, is also an approximation, the sun's disk extending over about 30 minutes of arc (half a degree) as viewed from the earth — this is called the sun's angular diameter. An approximation, but one made from that day till this by astronomers as being close to reality:

One of the postulates of spherical astronomy is that the earth can be considered as a mere point in relation to the spheres of the heavenly bodies. From this it follows that the sun's rays striking the earth are parallel, even at locations far removed from each other.^[6]

Eratosthenes needed the distance between Syene and Alexandria, which he took to be \( 5000 \) stades. There has been a great deal of discussion over the years as to how long a stade was. The term "stade" or "stadion" (Greek: στάδιον, Latin: stadium) was used over the centuries for widely varying distances and that should not be surprising in earlier eras without standardization or even stable states over time. The key point is that, for the sake of gauging Eratosthenes' error, it doesn't matter. Eratosthenes calculated that the circumference of the earth is \( 50 \) times the distance from Syene / Aswan to Alexandria, which is \( 843 \) km. (use this online calculator with Syene / Aswan at \( (24^{\circ} 05' 20'' \text{ N}, \; 32^{\circ} 53' 59'' \text{ E}) \) and Alexandria at \( (31^{\circ} 12' 00'' \text{ N}, \; 29^{\circ} 55' 00'' \text{ E}) \)). So the key calculation is:

\[ \text{circumference of earth} = (843 \text{ km.}) \times 50 = 42,150 \text{ km.}. \]

The actual figure for the polar circumference of the earth is \( 40,008 \) km., so:

\[ \text{Eratosthenes' error} = {{42,150 - 40,008} \over 40,008} = 5.4\% \hskip{12pt} \text{(high)} \]

Another way to look at this is that the proper multiplier is \( 40,008 / 843 = 47.46 \) rather that Eratosthenes' \( 50 \). Or that the correct angle is \( 843 / 40,008 \times 360^{\circ} = 7.59^{\circ} \) rather that Eratosthenes' \( 7.2^{\circ}. \)

Gratwick points out that deep vertical wells at Syene were likely used to tell when the sun was directly overhead. Vertical was not a problem even in those days with plumb lines — narrow might have been with the tools at hand, deep too with a low water table. But in principle you would know that the sun was overhead if you could see its reflection at the bottom. Modern timepieces were lacking, so noon had to be approximated at Alexandria when the shadow was measured.

Eratosthenes' experiment was an approximation, something he would have been well aware of. Some modern accounts diminish the accomplishment — why, he didn't even know that the earth is really closer to an oblate ellipsoid than an sphere! How anachronistic. The point is to determine if his method was sound (it was) and if his results were good (they were).

Eratosthenes did have scientific instruments — the sundial Cleomedes mentions was likely the the σκάφη / scaphe, a hemispherical bowl which had a vertical γνώμων / gnomon, or pointer, placed inside it. They were not machine-tooled or exact. That is the wonder of ancient astronomy, that they could do much of anything with their mostly eyeball techniques (more on this in Dicks, p. 9) That Eratosthenes could get the angle at Alexandria within a degree (and he did) is a small miracle, considering the tools at hand.

Gratwick explains how averages were probably taken on the scaphe to account for the half degree or so of the sun's angular diameter. Generally speaking, the ancients were capable of producing exacting scientific instruments, as the Romans did in engineering their impressive roads, straight and flat over long distances. Or take their aqueducts, including stretches falling at a grade of 1 in 5,000 at the time of Eratosthenes^[7]. Reverse-engineering the experiment, Eratosthenes was off by \( 7.59^{\circ} - 7.2^{\circ} = 0.39^{\circ} \), about \( 1/3^{\circ} \), so it seems his instruments were capable of accuracy on that order.

The next notable effort was that commissioned by the scholar-caliph al-Ma'mūn, who reigned at Baghdad from 813 till 833. al-Ma'mūn presided over an Islamic renaissance much like that later in Europe, featuring translation of and exegesis of the old Greek classics. By all accounts al-Ma'mūn had Eratosthenes' results from a thousand years earlier much in mind when he sent his astronomers into the field. Their method was to measure one degree of the earth's circumference by taking the angle of the North Star along a meridian in the desert. They concluded that one degree is \( 56 {2 \over 3} \) Arab miles (mil), leading to a circumference of \( 360 \times 56 {2 \over 3} = 20,400 \) Arab miles. Like with Eratosthenes' stadion, the question then becomes what exactly is an Arab mile. An influential article in 1892 concluded that \( 56 {2 \over 3} \) Arabic miles equates to \( 111.8 \) km, suspiciously close to the real value of \( 1^{\circ} = 111.3 \) km, though earlier investigators gave the value as anywhere between \( 104.7 \) km and \( 133.3 \) km. Whatever the exact truth, al-Ma'mūn's result is "probably rather good" in the words of Edward Kennedy^[8], probably better than Eratosthenes.

al-Bīrūnī Measures the Earth

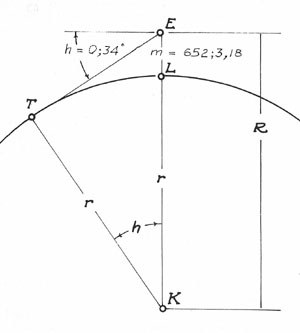
Around 1020, al-Bīrūnī took an entirely different approach. He measured the height of a hill rising from a flat desert and used trigonometry to calculate the radius of the earth. The diagram here is from Edward Kennedy's commentary on Al-Bīrūnī's Kitab Tahdid al-Amakin (“Determination of the Coordinates of Positions for the Correction of Distances Between Cities”)^[9]. Al-Bīrūnī speaks of a "high mountain"^[10], but it doesn't look like much of one at \( 652 \) cubits high (a cubit was about \( 0.5 \) meters). Note the height is labeled as \( m = 652;3,18 \), which equals \( 652 + 3/60 + 18/3600 = \) \( 652.055 \) cubits, using the sexagesimal notation used in astronomy since time immemorial for distances as well as angles and time. Angle \( h = 0;34 = 34' = 34/60^{\circ} \) is the angle of depression of the horizon from the top of the hill, as measured with an alidade. If \( r \) is the earth's radius, then \( \cos{h} = {r / (r+m)} \). Solving for \( r \) gives:
\[ r = {m \cdot {\cos{h} \over {1 - \cos{h}}}}. \]
The problem with this approach is the error introduced by the function:
\[ f(x) = {\cos{x} \over {1 - \cos{x}}}, \]
which has a very steep slope in the vicinity of zero (of course it is not defined at \( 0 \) — the vertical y-axis is an asymptote). That is, a small change in \( x \) around \( x = 34/60 \times \pi / 180 \) (converting to radians) leads to a big change in \( f(x) \), as shown in this chart:
\[ \begin{array}{l|l|cr}
x \; \text{ (deg)} & \hskip{30pt} x \text{ (rad)} & f(x)\\[6pt]
\hline
\;\; 33' & {33 \over 60} \cdot {\pi \over 180} = 0.0095993 & 21,704\\[4pt]
\;\; 34' & {34 \over 60} \cdot {\pi \over 180} = 0.0098902 & 20,446\\[4pt]
\;\; 35' & {35 \over 60} \cdot {\pi \over 180} = 0.0101811 & 19,294
\end{array} \]
Suppose the actual angle were \( 35' \) rather than the reported \( 34' \). Then the error in \( f(x) \) would be:
\[ \text{error } = {{20,446 - 19,294} \over 19,294} = {1152 \over 19,294} = 5.97\%, \]
which is larger than Eratosthenes' entire error, even assuming that \( m \) and \( \cos{h} \) are exactly correct. Yet Kennedy says that "for man-sized pre-telescopic instruments the accuracy of angular measurements can hardly be better than \( 0;5^{\circ} \)" — that is, \( 5/60^{\circ} = 1/12^{\circ} \), or five times the error just hypothesized. (Kennedy Commentary, p 37) al-Bīrūnī's gives two values for the earth's radius in different places: \( 12,803,337;2,9 \) cubits and \( 12,851,369;50,42 \) cubits. (Kennedy Commentary, p 143) From the foregoing, this is nonsense, accuracy within \( 10\% \) being very much in doubt, not to say accuracy to within \( 1 / 3600 \) cubit, the length of this unit too being open to question as with the stadion and Arab mile.

The point is not to deprecate the great al-Bīrūnī, whose real interest in the Kitab Tahdid was the accurate determination of cities' latitudes and longitudes, so faithful throughout the caliphate could be confident they were facing Mecca in prayer. This he did with a scientific rigor matching anything in Laplace, his simpler tools notwithstanding. The point is rather to highlight Eratosthenes' (and al-Ma'mūn's) prescience, indeed their wisdom, in looking at the inclination of celestial bodies to measure the earth.

First this from the Admiral's biographer Samuel Morison concerning the environment he faced in the 1480s:

The Portuguese were sailing southward, along Africa. Why not try sailing west, to Japan, China and India? What would prevent it? No flat-earth theory certainly; for of all the vulgar errors connected with Columbus, the most persistent and the most absurd is that he had to convince people "the world was round." Every educated man in his day believed the world to be a sphere, every European university so taught geography, and seamen, though they might doubt the practical possibility of sailing "down under" or holding on when you got there, knew perfectly well from seeing ships "hull down" (that is, seeing the mast in the distance before the lower body) and "raising" mountains as they approached, that the surface of the globe was curved.^[11]

In pressing his case for a western route to the Indies with the Portuguese and Spanish sovereigns, Columbus followed Marco Polo in adding some \( 30^{\circ} \) of longitude to Asia. He accepted al-Ma'mūn's figure of \( 56 {2 \over 3} \) miles for a degree, which had come to Europe through the influential Latin translation of al-Farghānī (Latin, Alfraganus), available since the twelfth century. As mentioned above, this is very close to being correct, assuming Arab miles. This implies that \( 56 {2 \over 3} \) Arab miles \( \sim 69.1 \) modern miles, the actual figure for one degree of arc along the earth's surface. In an epic sleight-of-hand, Columbus took the \( 56 {2 \over 3} \) as modern miles, thus underestimating a degree of arc (and the earth's circumference) by about \( 22\% \). All to make the case that the Indies aren't that far west, they can be reached by a \( 70' \) caravel in a few weeks. The combined error was massive, Japan being closer to Spain to the east than to the west. Columbus's sailors were at their wit's end just before landfall on the first voyage, the man was lucky beyond understanding. (Morison, p 86-87, 285)

The idea behind triangulation is that if you know one side of a triangle and all its angles, then you can solve the triangle, that is, find the other sides. If \( a, b, c \) are the three sides of a triangle, and \( A, B, C \) the corresponding angles, then the Law of Sines says that:
\[ a = {{b \cdot \sin{A}} \over {\sin{B}}}, \hskip{20pt} c = {{b \cdot \sin{C}} \over {\sin{B}}}.\]
If \( b \) is the known side, then sides \( a \) and \( c \) can be calculated by these formula using the sines of the angles. Consider a series of abutting triangles across the landscape, vertices at prominent high spots like hilltops, church steeples, even artificial obelisks if that's what it takes. The single measured line — the baseline — is the only distance needing to be measured as long as all the angles in the configuration are known, because the triangle containing the baseline can be solved, then a triangle abutting the first triangle can be solved, triangles adjacent to that one can be solved, and so on.

Two-triangle triangulation

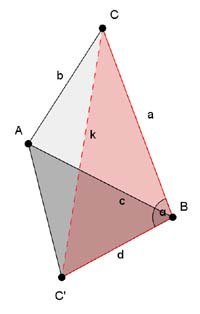
More trig can be brought into play to locate every vertex with respect to every other one. To see this, consider the simple two-triangle configuration pictured here — \( \bigtriangleup ABC \) above and \( \bigtriangleup ABC' \) below, sharing common side \( AB \). Suppose that side \( b \) is the baseline and all angles are known. \( a, c \), and the other lines in the two original triangles can be calculated as explained above. Angle \( \alpha \) between sides \( a \) and \( d \) is known, being the sum of two known angles, so now the Law of Cosines can be applied to the red triangle to calculate side \( k \):
\[ k^2 = a^2 + d^2 - 2ad \cos{\alpha}.\]
One more application of the Law of Sines leads to the other angles in the red triangle. So the two-triangle configuration can be replaced by a single triangle, though one of the original vertices is lost. Repeated applications of this method allow any two points in an initial configuration with any number of triangles to be located in a single triangle all of whose sides and angles are known.

The idea was developed by Willebrord Snellius (he of Snell's law) in his book Eratosthenes Batavus de terrae ambitûs vera quantitate (The Dutch Eratosthenes on the True Size of the Earth)^[12], published in 1617. Snellius overtly retraced Eratosthenes, introducing triangulation as a good way to measure distances on earth. He executed a large-scale triangulation in the Netherlands and produced a figure of \( 38,653 \) km. for the earth's circumference, \( 3.5\% \) low. His quadrant was accurate to approximately two minutes of arc. To appreciate his accomplishment, consider that triangulation much as he proposed it was the exclusive method used for large-scale surveying through the 1960s, when earth-orbiting satellites started coming into play.

Picard's triangulation

Snellius had a large quadrant, but still used eyeball techniques. Further progress required the incorporation of telescopic sights into the instruments — remember that Galileo's pioneering work using a telescope to identify Jupiter's moons was in 1610. The screw micrometer was another major innovation percolating as the 17th century advanced. Logarithms were crucial for extensive and exact trigonometric calculations; the key dates here being 1624 for Briggs's log table and 1628 for Vlacq's. Jean Picard used all these technologies in his triangulation of the meridian through Paris in 1668. He reported on his methods and results in Mesure de la Terre (Measure of the Earth)^[13] in 1671. He identifies the triangles in his triangulation, shown here, to the nearest five seconds of latitude and longitude; presumably his accuracy was within ten seconds. That's over ten times the accuracy of Snellius and his figure for the earth's circumference was \( 20,541,600 \) toises; that is, \( 40,036 \) km., considering that the French toise of the time equaled \( 1.949 \) meters. The earth is an oblate ellipsoid as Newton deduced from his theory of gravitation, squashed down a bit at the poles like a grapefruit. Its circumference at the equator is \( 40,075 \) km. and along a meridian \( 40,008 \) km., Picard's figure being a few kilometers from the average of those two. His error is \( 28 \) km., comparing his figure for the Paris meridian with the actual one, an error of \( 0.07\% \). Picard used his instruments to measure the latitude of two points at the ends of his triangulation by sighting celestial objects. His basic concept was identical to that of Eratosthenes; it's just that now the earth surveying and celestial measurements were being done in a highly refined way based on new technologies.

The design of Eratosthenes' experiment has held up as well as any in the history of science — the result too considering the tools at hand. al-Ma'mūn probably came closer a thousand years later with the same method and Snellius also with decidedly modern instruments and mathematics. It remained for Picard to finish the work 1900 years after Eratosthenes, that is an impressive record.

Mike Bertrand

July 29, 2017

^ 1. De Caelo, by Aristotle. Aristotle's main argument for the earth's being a sphere is philosophical and aesthetic, appealing to a form of gravity, that everything seeks the center and the elements of the earth did so at its time of formation. Secondly, eclipses of the moon suggest that an earth of circular cross-section interposes between sun and moon. Finally that different stars are visible at different locations on earth, suggesting that its surface is curved (also that the earth is small compared to the cosmos).

^ 2. Early Greek Astronomy to Arstotle, by D. R. Dicks, Cornell University Press (1970), SBN 8014-0561-0. "After the fifth century BC no Greek writer of any repute (with the exception of the atomists, Leucippus and Democritus, who held somewhat reactionary views on astronomy) conceived of the earth as anything other than a globe.", p. 72.

^ 3. Alexandria, Syene, Meroe: Symmetry in Eratosthenes' Measurement of the World, by A. S. Gratwick; Chapter 12 in The Passionate Intellect: Essays on the Transformation of Classical Traditions, by Lewis Ayres (ed.), Transaction Publishers (1995), ISBN 1-56000-210-7.

^ 4. Cleomedes' Lectures On Astronomy : A Translation of The Heavens, by Alan C. Bowen and Robert B. Todd, University of California Press (2004), ISBN 978-0520233256.

^ 5. Physical Science in the Middle Ages, by Edward Grant, Cambridge University Press (1971), ISBN 0-521-21862-4. See p. 5-12 for the handbook tradition. "There is no denying that a scientific dark age had descended on western Europe", p. 12. The foremost mathematical authorities in Europe for hundreds of years were Boethius (d. 524 / 525) and the Venerable Bede (d. 735); the first held forth on figurate numbers, the second on finger counting (Mathematics, by Michael S. Mahoney; Chapter 5 in Science in the Middle Ages, by David C. Lindberg (ed.), University of Chicago Press (1978), ISBN 0-226-48232-4).

^ 6. Measuring the Universe: Cosmic Dimensions from Aristarchus to Halley, by Albert Van Helden, University of Chicago Press (1985), ISBN 0-226-84881-7.

^ 7. Surveying Instruments of Greece and Rome, by M. J. T. Lewis, Cambridge University Press (2001), ISBN 0-521-79297-5. "a grade of \( 1 \) in \( 5,000 \)": p 115.

^ 8. Mathematical Geography, by Edward S. Kennedy; Chapter 5 in Encyclopedia of the History of Arabic Science, Vol 1, by Roshdi Rashad (ed.), Routledge (1996), ISBN 0-415-12410-7. The technical details in this paragraph come from this article.

^ 9. A Commentary upon Bīrūnī's Kitab Tahdid al-Amakin, by Edward S. Kennedy, American University of Beirut (1973).

^ 10. The Determination of the Coordinates of Positions for the Correction of Distances Between Cities: a Translation from the Arabic of al-Bīrūnī's Kitab Tahdid, by Jamil Ali, American University of Beirut (1967). "High mountain": p 188.

^ 11. Admiral of the Ocean Sea: A Life of Christopher Columbus, by Samuel Eliot Morison, Little, Brown and Company (1942). Quote is at p 45.

^ 12. Eratosthenes Batavus de terrae ambitûs vera quantitate (The Dutch Eratosthenes on the True Size of the Earth), by Willebrord Snellius (1617).

^ 13. Mesure de la Terre (Measure of the Earth), by Jean Picard (1671).