Chinese Remainder Theorem Calculator

A system of three congruences is shown on the right, but start with the simpler system:
\[ \begin{align*}
x &\equiv 1 \hspace{-.6em} {\pmod{2}}\\
x &\equiv 2 \hspace{-.6em} {\pmod{3}}.
\end{align*} \]
Values congruent \( \text{mod} \; 6 \) are certainly congruent \( \text{mod} \; 2 \) and \( \text{mod} \; 3, \) so in looking for an \( x \) solving both congruences simultaneously, it suffices to consider congruence classes \( \text{mod} \; 6 \) and in particular their smallest positive residues, namely \( 0, 1, 2, 3, 4, 5. \) We're seeking an odd number among those \( 6 \) since \( x \equiv 1{\pmod{2}}, \) one that is also congruent to \( 2 \; \text{mod} \; 3. \) \( x = 1 \) won't do, since \( 1 \equiv 1{\pmod{3}} \) neither will \( x = 3, \) since \( 3 \equiv 0{\pmod{3}}. \) \( x = 5 \) is the solution, since it satisfies both congruences, and it is the only solution \( \text{mod} \; 6. \)

Generally speaking, \( x \) can be congruent to \( 0 \) or \( 1 \) \( \text{mod} \; 2 \) and to \( 0, 1, \) or \( 2 \) \( \text{mod} \; 3 \), so there are \( 6 \) different combinations, and each one of them is congruent to a different solution \( \text{mod} \; 6 \). This situation is characteristic and exemplifies the Chinese Remainder Theorem. Any number of congruences can be brought in and there will be exactly one solution mod their product as long as the moduli are pairwise relatively prime.

Let \(n_1, n_2, \ldots n_r \) be positive integers that are pairwise relatively prime and \(a_1, a_2, \ldots a_r \) any integers. Then the system of congruences \[ \begin{align*} x &\equiv a_1 \hspace{-.6em} {\pmod{n_1}}\\ x &\equiv a_2 \hspace{-.6em} {\pmod{n_2}}\\ &\vdots\\ x &\equiv a_r \hspace{-.6em} {\pmod{n_r}}\\ \end{align*} \] has a unique simultaneous solution \( \text{mod} \) the product \( n = n_1 n_2 \cdots n_r. \)

Proof. For \( k = 1, 2, \ldots r, \) put \( N_k = n / n_k; \) that is, \( N_k \) is the product of all the \( n_i \) except for the \( k^{\text{th}} \) one. For each \( k, \) let \( x_k = N_k^{-1} \pmod{n_k}, \) which exists since \( N_k \) and \( n_k \) are relatively prime by construction. Another way of putting this is that \( N_k x_k \equiv 1{\pmod{n_k}}. \) Note that \( x_k \) is unique \( \text{mod} \; n_k\), so we can choose \( x_k \) between \( 0 \) and \( n_k - 1. \) Put:

\[ x' = a_1 N_1 x_1 + a_2 N_2 x_2 + \cdots + a_r N_r x_r. \]

The claim is that \( x' \) is the unique solution of the system \( \text{mod} \; n. \) Note that \( n_1 \) divides all the \( N_k \) except \( N_1 \) and consequently \( a_k N_k x_k \equiv 0 {\pmod{n_1}} \) for \( k \neq 0, \) and so:

\[ x' \equiv a_1 N_1 x_1 + 0 \equiv a_1 \cdot 1 \equiv a_1 \hspace{-.6em} {\pmod{n_1}}. \]

In exactly the same way, \( x' \) satisfies all the other congruences. To establish uniqueness, suppose that \( x'' \) is another solution. Then for all \( k \):

\[ \begin{align*}
x' &\equiv x'' \equiv a_k \hspace{-.6em} {\pmod{n_k}},\\
\therefore x' &- x'' \equiv 0 \hspace{-.6em} {\pmod{n_k}}.
\end{align*} \]

That is, \( n_k | x' - x'' \) for all \( k, \) and so \( n = n_1 n_2 \cdots n_r | x' - x'' \) since the \( n_i \) are relatively prime and \( x' \equiv x'' {\pmod{n}}. \) QED.

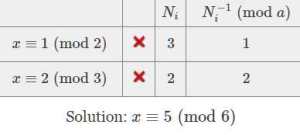
The nice thing about this proof is that it provides a blueprint for solving a system. Go back to the simple system at the start, entering it into the calculator and solving like this:

• Enter \( 1,2 \) in the text field, click Add Congruence.
• Enter \( 2,3 \) in the text field, click Add Congruence.
• Click Solve.

Putting \( a_1 = 1 \) and \( a_2 = 2, \) and plugging in the key auxiliary values derived by the calculator:

\[ x' = a_1 N_1 N_1^{-1} + a_2 N_2 N_2^{-1} = 1 \cdot 3 \cdot 1 + 2 \cdot 2 \cdot 2 = 3 + 8 = 11 \equiv 5 \hspace{-.6em} {\pmod{6}}.\]

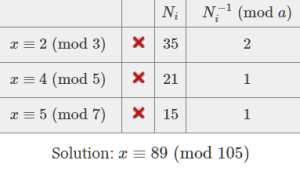
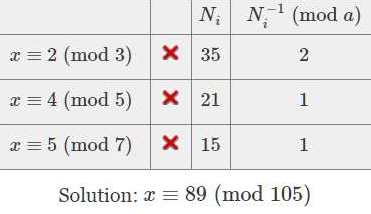
Let's try another. In the calculator, you can remove a congruence by clicking the little red X in that row. So do that for any congruences currently showing to clear the slate. Then enter this system:

• Enter \( 2,3 \) in the text field, click Add Congruence.
• Enter \( 4,5 \) in the text field, click Add Congruence.
• Enter \( 5,7 \) in the text field, click Add Congruence.
• Click Solve.

Were you doing this by hand, you'd need to solve \( 35 x \equiv 1 {\pmod{3}}, \) which looks forbidding, but not when you consider that \( 35 \equiv 2 {\pmod{3}}, \) so it amounts to solving \( 2 x \equiv 1 {\pmod{3}}, \) which trial-and-error reduces to \( x \equiv 2 {\pmod{3}}. \) The other two reciprocals are easy too, in fact they're both \( 1. \) The final solution is:

\[ x' = \sum_1^3{a_i N_i N_i^{-1}} = 2 \cdot 35 \cdot 2 + 4 \cdot 21 \cdot 1 + 5 \cdot 15 \cdot 1 = 299 \equiv 89 \hspace{-.6em} {\pmod{3 \cdot 5 \cdot 7}}. \]

Simple calculations check that \( x = 89 \) solves all three congruences — for example, \( 89 \equiv 5 {\pmod{7}}. \)

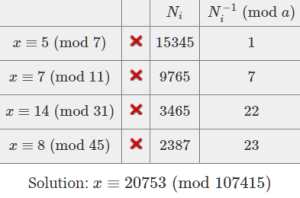
Calculating the inverses by trial-and-error becomes onerous for systems with large moduli. Take this example where we need to solve \( 3465 x \equiv 1 {\pmod{31}} \) in connection with the third congruence, or \( 24 x \equiv 1 {\pmod{31}}, \) after reducing \( 3465 \) to \( 24 {\pmod{31}}. \) The general scheme for calculating inverses is the Euclidean Algorithm, which for any \( u \) and \( v, \) provides a way to calculate multipliers \( a \) and \( b \) such that:

\[ au + bv = \text{gcd}(u, v). \]

Let's proceed by example with \( u = 24 \) and \( v = 31, \) so \( \text{gcd}(u, v) = \text{gcd}(24, 31) = 1, \) as it always will be in this setup. Applying the Euclidean Algorithm to \( 31 \) and \( 24 \):

\[ \begin{align*}
31 &= 1 \cdot 24 + 7\\
24 &= 3 \cdot 7 + 3\\
7 &= 2 \cdot 3 + 1\\
\end{align*} \]

Work from the bottom up in this calculation to express \( 1 \) as a linear combination of \( 7 \) and \( 3, \) then \( 24 \) and \( 7, \) and finally \( 31 \) and \( 24 \):

\[ \begin{align*}
1 &= 7 - 2 \cdot 3\\
&= 7 - 2 \cdot (24 - 3 \cdot 7)\\
&= 7 \cdot 7 - 2 \cdot 24\\
&= 7 \cdot (31 - 24) - 2 \cdot 24\\
&= 7 \cdot 31 - 9 \cdot 24.
\end{align*} \]

That is, \( 1 = 7 \cdot 31 - 9 \cdot 24, \) so \( (- 9) \cdot 24 \equiv 22 \cdot 24 \equiv 1 {\pmod{31}} \) showing that \( 24^{-1} \equiv 22{\pmod{31}}. \)

Here is a graphical representation of the system:

\[ \begin{align*}
x &\equiv a_1 \hspace{-.6em} {\pmod{2}},\\
x &\equiv a_2 \hspace{-.6em} {\pmod{3}},\\
x &\equiv a_3 \hspace{-.6em} {\pmod{5}}.
\end{align*} \]

All three \( N_i^{-1} = 1 \) for this combination of moduli, so the general solution is:

\[ x' = \sum_1^3{a_i N_i N_i^{-1}} = a_1 \cdot 15 \cdot 1 + a_2 \cdot 10 \cdot 1 + a_3 \cdot 6 \cdot1 = 15a_1 + 10a_2 + 6a_3 \hspace{-.6em} {\pmod{30}}. \]

There are \( 2 \cdot 3 \cdot 5 = 30 \) different configurations for the clocks, taking all combinations of settings into account. The Chinese Remainder Theorem says that the set of configurations is in one-to-one correspondence with values \( \text{mod } 30, \) and this little app lets you explore the correspondence.

Mike Bertrand

January 7, 2017