Cauchy's Memoire Sur le Nombre des Valeurs

MM. Lagrange and Vandermonde are, I believe, the first who considered functions of several variables relative to the number of values they can return, when these variables are substituted for each other.

They gave several interesting theorems relating to this subject in two papers published in 1771, one in Berlin, the other in Paris. Since that time, some Italian mathematicians have been busy successfully pressing this matter, particularly M. Ruffini, who recorded the results of his research in Volume XII of the Memoirs of the Italian Society, and in his Theory of Numerical Equations. One of the most remarkable consequences of the work of these mathematicians, is that with a given number of letters one cannot always form a function which returns a predetermined number of values. The characteristics causing this failure are not always easy to grasp; but one can at least, for a given number of letters, set limits that the number of values may not exceed, and further determine a large number of exceptions. I will discuss in this paper the most important things that have already been found on this subject, and what my own research has led me to add. I will examine more specifically the case where the number of values of a function is assumed to be smaller than the number of letters, because it is knowledge of functions of this kind that is most useful in analysis.

---

Consider a function of several variables, and assume that these variables are substituted with each other one or more times in succession. If the function is of the kind called symmetric, the value will not change as a result of such transpositions between variables it contains; but if it is not symmetric, multiple different values can be obtained by applying these same transpositions and the number of different values is determined by the nature of the function in question. If the functions are divided into different orders depending on the number of variables they contain, so that a second order function is one that contains two variables, a function of the third order one that contains three, and so on, it will be easy to recognize that there is a necessary connection between the number of values that can be obtained from a non-symmetric function and the order of that same function. For example, a function of the second order can never take more than two values, which may be derived from one another by a transposition of the two variables that compose it. Similarly, a function of the third order cannot take more than six values; a function of the fourth order no more than twenty-four values, and so on. In general, the maximum number of values that can be obtained from a function of order n will clearly be equal to the product:

\[ 1 . 2 . 3 ... n; \]

because this product represents the number of different ways of arranging the variables which make up the function. This already limits the number of values which may not be exceeded: but for each order, one may form functions for which the number of values is equal to a whole number below this limit. A little reflection is enough to show that no number below the limit can fulfill the required condition, at least if it is not a divisor of this limit. This is easily verified by the following considerations.

Let \( K \) be any function of order \( n \), and denote by \( a_1, a_2 \cdots a_n \) the variables it contains. If one writes the variables in question one after the other, or, equivalently, just the indices, in the order they appear, from left to right, and taking care to write each index only once, then there will be a permutation of these indices which has a necessary relationship with the function \( K \). For example, let the function \( K \) be of the fourth order, and equal to:

\[ a_1 a_2^m \cos(a_4) + a_4 \sin(a_3), \]

then the related permutation on \( K \) would be:

\[ 1 \ . 2 \ . 4 \ . 3. \]

If below the permutation on \( K \), one writes another permutation formed with the indices \( 1, 2, 3 \cdots n \), and successively replaces in the function \( K \) each of the indices in turn which compose the upper permutation by the corresponding index in the lower permutation, then there appears a new value for \( K \) which may or may not be equivalent to the first, and the permutation for that new value of \( K \) will obviously be the lower permutation just mentioned. By this means one can obtain the values of \( K \) for the various permutations that can be formed with the indices \( 1, 2, 3 \cdots n \); and if one represents them by

\[ K, K', K'', \cdots \]

then the number of values in question will be the product

\[ 1 . 2 . 3 \cdots n \]

and together they provide all the possible values of the function \( K \). To derive these two values from each other, it will suffice to form the permutations on these two values, and to substitute for the indices of the first permutation the corresponding indices from the second one. To indicate this substitution, I will write both permutations in enclosing parentheses, placing the first over the second: thus, for example, the substitution

\[ \begin{pmatrix}
1 \ . 2 \ . 4 \ . 3 \\
2 \ . 4 \ . 3 \ . 1 \\
\end{pmatrix} \]

indicates that in \( K \) one should substitute index 2 for index 1, index 4 for index 2, index 3 for index 4, and index 1 for index 3. Therefore, if one assumes, as above,

\[ K = {a_1 a_2^m \cos(a_4) + a_4 \sin(a_3)}, \]

denoting by \( K' \) the new value of \( K \) obtained by the substitution

\[ \begin{pmatrix}
1 \ . 2 \ . 4 \ . 3 \\
2 \ . 4 \ . 3 \ . 1 \\
\end{pmatrix} \]

one will have

\[ K' = {a_2 a_4^m \cos(a_3) + a_3 \sin(a_1)}. \]

To shorten this, in the following I will represent permutations themselves by capital letters. Thus, if one denotes the permutation

\[ 1 \ . 2 \ . 4 \ . 3 \hskip{20px} \text{ by } \hskip{20px} A_1, \]

and the permutation

\[ 2 \ . 4 \ . 3 \ . 1 \hskip{20px} \text{ by } \hskip{20px} A_2, \]

then the substitution

\[ \begin{pmatrix}
1 \ . 2 \ . 4 \ . 3 \\
2 \ . 4 \ . 3 \ . 1 \\
\end{pmatrix} , \]

is indicated in the following manner,

\[ \begin{pmatrix}
A_1 \\
A_2 \\
\end{pmatrix} \]

That said, \( K \) being an arbitrary function of order \( n \), denote by \( N \) the product \( 1 . 2 . 3 \cdots n \) and let

\[ A_1, A_2, A_3, \cdots A_N, \]

be all \( N \) permutations that can be formed with the indices \( 1, 2, 3, \cdots n \), where \( N \) is the total number of values of the function \( K \) under the action of all these permutations. Let

\[ K_1, K_2, K_3 \cdots K_N \]

be these corresponding values. If they are all different from each other, then the number of different values taken by the function is \( N \), but in the contrary case where the number of such values taken is less than \( N \), the number of values is necessarily a divisor of \( N \), as will be seen.

Assume that, among the possible values

\[ K_1, K_2, K_3 ..... K_N \]

taken by the function, some become equal to each other, so that one has, for example,

\[ K_{\alpha} = K_{\beta} = K_{\gamma} = \cdots . \]

Denote by \( M \) the total number of values \( K_{\alpha}, K_{\beta}, K_{\gamma} \), etc., which are equal to each other. The permutations on these values, \( A_{\alpha}, A_{\beta}, A_{\gamma} \), etc., will also be equal in number to \( M \). To derive these permutations individually from \( A_{\alpha} \), for example, it is sufficient to exchange between them in a certain way so that the indices of that permutation occupy appropriate places; and it is easily seen that if these changes do not affect the corresponding value \( K_{\alpha} \) of the function \( K \), then significance lies not in the values of the indices, but in the space that each occupies in its respective permutation.

That said, let \( K_{\lambda} \) be new value of \( K \), which is not equal to \( K_{\alpha} \): and still denote by \( A_{\lambda} \) the permutation on \( K_{\lambda} \). If one subjects indices simultaneously occupying the same positions in permutations \( A_{\alpha} \) and \( A_{\lambda} \) to the changes just discussed, then the second permutation \( A_{\lambda} \) is found successively changed to several others — \( A_{\mu}, A_{\nu} \), and so on, while the first \( A_{\alpha} \) becomes successively \( A_{\beta}, A_{\gamma} \), and so on; and according to the principle above, it is clear that the equation

\[ K_{\alpha} = K_{\beta} = K_{\gamma} = \cdots . \]

results in

\[ K_{\lambda} = K_{\mu} = K_{\nu} = \cdots . \]

It is easy to conclude that among the values of \( K \) for all possible permutations, that is,

\[ K_1, K_2, K_3 \cdots K_N, \]

the number that will be equivalent to \( K_{\lambda} \) is the same as the number of values equivalent to \( K_{\alpha} \). Thus, if one represents by \( R \) the total number of substantially different values of the function \( K \), where \( M \) is the number of values equal to \( K_{\alpha} \), then \( R \cdot M \) will be the total number of values for all the permutations. We thus obtain \( {R \cdot M} = N \), and consequently:

\[ R = {N \over M}. \]

So \( R \), the number of different values of the function \( K \), must be a divisor of \( N \); that is to say, of the product \( 1 . 2 . 3 \cdots n \). The theorem which we present as the first fact in the theory of combinations was already known; but it was necessary to recall for understanding what follows. In short, I now call the index of the function \( K \) the number \( R \) which indicates how many essentially different values this function can take, and I call the number \( M \) the indicative divisor which divides into \( N \), the product of the indices \( 1, 2, 3 \cdots n \) contained in the function, to get the index of the function itself.

We have seen that the number of different values of a function of order \( n \) is necessarily a divisor of the product,

\[ N = {1 . 2 . 3 ... n}. \]

The smallest divisor of the product is always equal to 2, and it is easy to ensure that for any order, functions can be formed which have only two different values. Vandermonde has the means to compose functions of this type. In general, to form a function of order \( n \) with the quantities

\[ a_1, a_2 \cdots a_n \]

whose index is equal to 2, it suffices to consider the positive part or the negative part of the product

\[ (a_1 - a_2)(a_1 - a_3) \cdots (a_1 - a_n)(a_2 - a_3) \cdots (a_2 - a_n) \cdots (a_{n-1} - a_n), \]

where the factors with the differences of the variables \( a_1, a_2, \cdots a_n \) are taken in pairs.

Indeed, suppose that after having developed this product, one represents by \( P \) the sum of positive terms, and by \( Q \) the sum of negative terms, then the product in question is represented by:

\[ P - Q; \]

and as this can never change value, but only sign, under any substitutions made between the indices of the variables contained therein, the substitutions in question can only transform \( P - Q \) into \( Q - P \), that is to say, change \( P \) into \( Q \), and vice versa. \( P \) and \( Q \) are the two values of the function that can take only each value of P and Q as values. Assuming \( n = 3 \), you find

\[ P = {a_1^2 a_2 + a_2^2 a_3 + a_3^2 a_1} \\
Q = {a_1 a_2^2 + a_2 a_3^2 + a_3 a_1^2}. \]

We would still arrive at similar conclusions if we had multiplied the product

\[ (a_1 - a_2)(a_1 - a_3) \cdots (a_1 - a_n)(a_2 - a_3) \cdots (a_2 - a_n) \cdots (a_{n-1} - a_n) \]

by any symmetric function of the quantities

\[ a_1, a_2 \cdots a_n. \]

What has been noted in relation to the divisor \( 2 \) in the product \( 1 . 2 . 3 \cdots n \) is not true in general with respect to other divisors of the product, and it is not always possible to form a function of order \( n \), the number of whose different values are one of these divisors chosen at will. Suppose, for example, that \( K \) is a type of function with only three different values. If \( n \) is equal to 3, one will find an infinite number of functions fulfilling the required condition, including:

\[ a_1 a_2 + a_3, \\
a_1 (a_2 + a_3), \\
etc. \]

One could also form the functions in the case that n equals 4, for example:

\[ a_1 a_2 + a_3 a_4, \\
(a_1 + a_2)(a_3 + a_4), \\
etc. \]

But if \( n \) is equal to 5, or exceeds 5, the situation is not similar: you can not even, in this case, form functions with only four values. Both propositions have been demonstrated by M. Paolo Ruffini, in the Memoirs of the Italian Society Volume XII, and in his Theory of Equations. Having been led by this numerical research to take up the theory of combinations, I came to the demonstration of a more general theorem containing the two earlier results, and which determines a limit below which the number of values of a non-symmetric function of order \( n \) can never go, without being equal to 2. This theorem can be stated as follows:

The number of different values of a non-symmetric function of \( n \) variables cannot be less than the largest prime number \( p \) contained in \( n \) without being equal to 2.

Since, to prove this theorem, it is necessary to know the nature of the operation that I designated as a substitution, I will start by developing this subject.

Let \( K \) be a function of order \( n \); let the index of \( R \) be the number of essentially different values it can take under the substitution operations of the variables of which it is composed. Finally denote by \( N \) the product \( 1 . 2. 3 \cdots n \), \( R \) being necessarily a divisor of \( N \) which I can represent by

\[ N \over M, \]

where \( M \) is the indicative divisor of the function \( K \). That said, let \( A_1, A_2, ... A_N \) be the \( N \) permutations that can be formed with indices contained in \( K \), and denote by

\[ K_1, K_2, \cdots K_N \]

the corresponding values of the same function; to derive one of these values from the other, or equivalently the permutations which correspond to them — for example, \( A_1 \) and \( A_2 \) — it will suffice to replace respectively the indices included in the permutation \( A_1 \) by the corresponding indices in permutation \( A_2 \). This operation, which I call substitution, will, according to established conventions, be indicated as follows,

\[ \begin{pmatrix}
A_1 \\
A_2 \\
\end{pmatrix} \]

The two permutations \( A_1 \) and \( A_2 \) will be called respectively the first and second term of this substitution. Swap the first term \( A_1 \) of this substitution, so that the order of the indices \( 1, 2, 3, \cdots \) is interwoven in the same way that the corresponding indices are ordered in \( A_2 \). It is therefore possible to give successively the first term of each proposed substitution of the permutations \( A_1, A_2, A_3, \cdots A_N \) and thus to put them below a number equal to \( N \) different forms which are all equivalent to each other.

I will say that a substitution is the product of many others, when it gives the same result when the others are applied successively. For example, if by applying successively to the permutation \( A_1 \) the two substitutions \( \Large \bigl(\begin{smallmatrix} A_2 \\ A_3 \end{smallmatrix}\bigr) \) and \( \Large \bigl(\begin{smallmatrix} A_4 \\ A_5 \end{smallmatrix}\bigr) \), you obtain the resulting permutation \( A_6 \); then the substitution \( \Large \bigl(\begin{smallmatrix} A_1 \\ A_6 \end{smallmatrix}\bigr) \) is equivalent to the product of the two others, and I will show this equivalence as follows:

\[ \begin{pmatrix}
A_1 \\
A_6
\end{pmatrix} =
\begin{pmatrix}
A_2 \\
A_3
\end{pmatrix}
\begin{pmatrix}
A_4 \\
A_5
\end{pmatrix} \]

An identical substitution is one with two terms that are identical. The substitutions

\[ \begin{pmatrix}
A_1 \\
A_1
\end{pmatrix} ,
\begin{pmatrix}
A_2 \\
A_2
\end{pmatrix}
\cdots
\begin{pmatrix}
A_N \\
A_N
\end{pmatrix} \]

are all identical.

I will say that two substitutions are contiguous when the second term of the first is equal to the first term of the second. The two contiguous substitutions \( \Large \bigl(\begin{smallmatrix} A_1 \\ A_2 \end{smallmatrix}\bigr) \), \( \Large \bigl(\begin{smallmatrix} A_2 \\ A_3 \end{smallmatrix}\bigr) \) acting successively give the same result as the single substitution \( \Large \bigl(\begin{smallmatrix} A_1 \\ A_3 \end{smallmatrix}\bigr) \), and therefore:

\[ \begin{pmatrix}
A_1 \\
A_3
\end{pmatrix} =
\begin{pmatrix}
A_1 \\
A_2
\end{pmatrix}
\begin{pmatrix}
A_2 \\
A_3
\end{pmatrix} \]

You even have, in general:

\[ \begin{pmatrix}
A_1 \\
A_r
\end{pmatrix} =
\begin{pmatrix}
A_1 \\
A_2
\end{pmatrix}
\begin{pmatrix}
A_2 \\
A_3
\end{pmatrix}
\begin{pmatrix}
A_3 \\
A_4
\end{pmatrix} \cdots
\begin{pmatrix}
A_{r-1} \\
A_r
\end{pmatrix} \]

Finally, I would say that a substitution is derived from another, or is a power of another, if it is equivalent to the other repeated several times. I will show the power \( r \) of a substitution \( \Large \bigl(\begin{smallmatrix} A_1 \\ A_2 \end{smallmatrix}\bigr) \) in the following way:

\[ \begin{pmatrix}
A_1 \\
A_2
\end{pmatrix}^r \]

When contiguous substitutions

\[ \begin{pmatrix}
A_1 \\
A_2
\end{pmatrix} ,
\begin{pmatrix}
A_2 \\
A_3
\end{pmatrix} ,
\begin{pmatrix}
A_3 \\
A_4
\end{pmatrix} , \cdots
\begin{pmatrix}
A_{r-1} \\
A_r
\end{pmatrix} \]

are all equivalent to each other, then:

\[ \begin{pmatrix}
A_1 \\
A_2
\end{pmatrix}^r =
\begin{pmatrix}
A_1 \\
A_2
\end{pmatrix}
\begin{pmatrix}
A_2 \\
A_3
\end{pmatrix}
\begin{pmatrix}
A_3 \\
A_4
\end{pmatrix} \cdots
\begin{pmatrix}
A_{r-1} \\
A_r
\end{pmatrix} =
\begin{pmatrix}
A_1 \\
A_r
\end{pmatrix} \]

Suppose the substitution \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \) is applied repeatedly to the permutation \( A_1 \), so that the substitution is first applied to \( A_1 \), giving permutation \( A_2 \) as the result, then the substitution is applied to \( A_2 \), giving permutation \( A_3 \) as the result, and so on. The series of permutations

\[ A_1, A_2, A_3, etc. \cdots \]

will necessarily be composed of a finite number of terms; and if one puts m for the number of terms and \( A_m \) for the final permutation obtained, then the substitution \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \) applied to the last permutation reproduces anew the term \( A_1 \). That said, if one arranges the permutations in a circle, or rather a regular polygon, the permutations

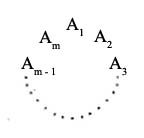
\[ A_1, A_2, A_3, \cdots A_{m-1}, A_m \]

look as follows:

then all substitutions that can be formed with two permutations taken following one another from east to west in the polygon in question will be equivalent to each other and to \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \), and all those that one can form with two permutations separated from one another by a number \( r \) of sides in the same polygon will be equivalent to a power \( r \) of the substitution \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \).

It goes like this:

\[ \begin{pmatrix}
A_s \\
A_t
\end{pmatrix} =
\begin{pmatrix}
A_1 \\
A_2
\end{pmatrix} =
\begin{pmatrix}
A_2 \\
A_3
\end{pmatrix} = \hskip{10pt} \text {etc. } \cdots \hskip{10pt} =
\begin{pmatrix}
A_m \\
A_1
\end{pmatrix} , \]

\[ \begin{pmatrix}
A_s \\
A_t
\end{pmatrix}^2 =
\begin{pmatrix}
A_1 \\
A_3
\end{pmatrix} =
\begin{pmatrix}
A_2 \\
A_4
\end{pmatrix} = \hskip{10pt} \text {etc. } \cdots \hskip{10pt} =
\begin{pmatrix}
A_m \\
A_2
\end{pmatrix} , \]

\[ \begin{pmatrix}
A_s \\
A_t
\end{pmatrix}^3 =
\begin{pmatrix}
A_1 \\
A_4
\end{pmatrix} =
\begin{pmatrix}
A_2 \\
A_5
\end{pmatrix} = \hskip{10pt} \text {etc. } \cdots \hskip{10pt} =
\begin{pmatrix}
A_m \\
A_3
\end{pmatrix} , \]

\[ \hskip{-120pt} \text{etc.} \cdots \]

\[ \begin{pmatrix}
A_s \\
A_t
\end{pmatrix}^m =
\begin{pmatrix}
A_1 \\
A_1
\end{pmatrix} =
\begin{pmatrix}
A_2 \\
A_2
\end{pmatrix} = \hskip{10pt} \text {etc. } \cdots \hskip{10pt} =
\begin{pmatrix}
A_m \\
A_m
\end{pmatrix} , \]

\[ \begin{pmatrix}
A_s \\
A_t
\end{pmatrix}^{m+1} =
\begin{pmatrix}
A_1 \\
A_2
\end{pmatrix} =
\begin{pmatrix}
A_2 \\
A_3
\end{pmatrix} = \hskip{10pt} \text {etc. } \cdots \hskip{10pt} =
\begin{pmatrix}
A_m \\
A_1
\end{pmatrix} , \]

\[ \hskip{-125pt} \text{etc.} \cdots \]

It follows from these considerations 1st that the power m of the substitution \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \) is equivalent to the substitution \( \Large \bigl(\begin{smallmatrix} A_1 \\ A_1 \end{smallmatrix}\bigr) \) itself; 2nd, that if \( x \) is any integer, then \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr)^{\normalsize mx} \) will again be that same substitution; 3rd that by the same hypothesis, the substitutions \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr)^{\normalsize mx+\gamma} \) and \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr)^{\normalsize \gamma} \) are equivalent; 4th that the notation \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr)^{\normalsize 0} \) indicates the identity substitution; 5th that of all the distinct substitutions derived from \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \) by taking powers, only those of power less than m are different, namely, the substitutions:

\[ \begin{pmatrix}
A_1 \\
A_1
\end{pmatrix} ,
\begin{pmatrix}
A_1 \\
A_2
\end{pmatrix} ,
\begin{pmatrix}
A_1 \\
A_3
\end{pmatrix} , \cdots
\begin{pmatrix}
A_1 \\
A_m
\end{pmatrix} . \]

The number of such substitutions, like the permutations \( A_1, A_2, A_3, \cdots A_m \), equals \( m \). This number will be called the degree of substitution \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \). Repeatedly applying substitution \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \) to the permutation \( A_1 \), one starts by getting more permutations \( A_1, A_2, A_3, \cdots A_m \); and when it comes to this point, the same permutations recur in the same order in a periodic manner. That is why I say that the previous permutations form a period corresponding to the substitution \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \). That said, the degree of substitution \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \) indicates the smallest positive power equivalent to the identity substitution, and the number of permutations included in the period resulting from the substitution by applying a specific permutation.

The simplest way to represent a period is to arrange the permutations that compose it around a circle, or rather a regular polygon, as we have already done above.

I would say that the circle formed, as we have said, is one of the circles of permutations corresponding to the substitution \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \). Any substitution having as terms two permutations included in this circle is one of the powers of the substitution \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \).

Given the previous circle or polygon corresponding to the substitution \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \); to derive a polygon corresponding to the substitution \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \), one simply joins the vertices of the given polygon from \( r \) to \( r \), going east to west, and writes permutations encountered in the order in which they arise. When \( r \) and \( m \) are relatively prime, one moves in this way along the vertices of the first polygon so that the second polygon contains all permutations included in the first; consequently the substitution \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr)^{\normalsize r} \) is of degree \( m \), as is the given substitution \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \); and the second substitution may then be considered as a power of the other. This fact always holds where \( m \) is a prime number, whatever the value of \( r \).

If one successively applies the substitution \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \) to different values of the function \( K \) or, what amounts to the same thing, to the permutations:

\[ A_1, A_2, A_3, \cdots A_N \]

to which they correspond, one gets a whole number equal to \( N/m \) of polygons or circles different from each other, which are each composed of \( m \) different permutations.

That said, designate under the name of equivalent permutations those that correspond to equivalent values ​​of the function \( K \); the permutations equivalent to \( A \) are assumed to be \( M \) in number, and it is evident that for \( M > N/m \), it is possible, among all circles thus formed, to find at least one that contains two equivalent permutations of those in question. Let \( A_x, A_y \) be these two permutations, the substitution \( \Large \bigl(\begin{smallmatrix} A_x \\ A_y \end{smallmatrix}\bigr) \) one of the powers of the substitution \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \), and if \( m \) is a prime number then \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \) is a power of the substitution \( \Large \bigl(\begin{smallmatrix} A_x \\ A_y \end{smallmatrix}\bigr) \). Moreover, the two permutations \( A_x , A_y \) being equivalent to each other and to the permutation \( A_1 \), the the substitution \( \Large \bigl(\begin{smallmatrix} A_x \\ A_y \end{smallmatrix}\bigr) \) will not change the value \( K_1 \) of the function \( K \). As a result, the same value will not be changed by the substitution \( \Large \bigl(\begin{smallmatrix} A_x \\ A_y \end{smallmatrix}\bigr) \) repeated several times; it will therefore not be changed by the substitution \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \) if \( m \) is a prime number. If one represents by \( p \) the largest prime number contained in \( n \), it can be assumed in the foregoing that

\[ m = p. \]

We are thus led by the above considerations to this remarkable result, that relative to the function \( K \), we cannot assume that \( M > N/p \), or, equivalently, that \( R < p \), unless we assume at the same time that the value \( K_1 \) of this function cannot be changed by any substitutions of degree \( p \). We see that to satisfy this condition, we must make the function symmetric or assume

\[ R = 2. \]

Before going further, it is necessary to examine with some care the nature of the substitutions of degree p, that can be formed with indices \( 1, 2, 3, \cdots n \).

We observe first of all that if a substitution \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \) is formed by two permutations taken at will from

\[ A_1, A_2, A_3, \cdots A_N, \]

where the two terms \( A_s, A_t \) contain corresponding indices that are equal, respectively, one can conveniently remove these indices and retain only those corresponding indices which are unequal. For example, if one lets \( n = 5 \), then the two substitutions

\[ \begin{pmatrix}
1 \ . 2 \ . 3 \ . 4 \ . 5 \\
2 \ . 3 \ . 1 \ . 4 \ . 5 \\
\end{pmatrix} and
\begin{pmatrix}
1 \ . 2 \ . 3 \\
2 \ . 3 \ . 1 \\
\end{pmatrix} \]

are equivalent to each other. I say that a substitution has been reduced to its simplest form, when one removes all terms where corresponding indices are equal.

Now let \( \alpha, \beta, \gamma, \cdots \zeta, \eta \) be several indices, \( p \) in number, taken from \( 1, 2, 3, \cdots n \); and suppose that the substitution \( \Large \bigl(\begin{smallmatrix} A_s \\ A_t \end{smallmatrix}\bigr) \) reduces to a simple expression of the form

\[ \begin{pmatrix}
\alpha \ \beta \ \gamma \ \cdots \ \zeta \ \eta \\
\beta \ \gamma \ \delta \ \cdots \ \eta \ \alpha
\end{pmatrix} , \]

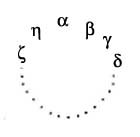
so that to derive the second term from the first, it is enough to arrange them on a circle, or rather a regular polygon, displaying the indices \( \alpha, \beta, \gamma, \cdots \zeta, \eta \) like this, then replace each index by the next one in place when rotating ​​the polygon east to west. It is easy to see that to get the power \( r \) of the given substitution, simply replace each index of the polygon by the one taking its place after rotating by \( r \) sides, when turning the polygon east to west. If one wants to obtain the identity substitution in this way, it will be assumed that \( r \) equals \( p \) or a multiple of \( p \); because each index will return to its original position after making one or more turns around the polygon. It follows that the degree of the given substitution is equal to \( p \). I'll denote as the indicated polygon or indicated circle the polygon or circle made up of the indices from this substitution and will designate this by the name circular substitution. For a substitution to be circular, it suffices that after being reduced to its simplest expression, one can review all its indices, comparing as pairs the indices that correspond within the two terms. The degree of circular substitution is always equal to the number of indices it contains.

Let

\[ \begin{pmatrix}
\alpha \ \beta \ \gamma \ \delta \ \cdots \ \zeta \ \eta \\
\beta \ \gamma \ \delta \ \epsilon \cdots \ \eta \ \alpha
\end{pmatrix} \]

be a circular substitution of degree \( p \),

\[ \begin{pmatrix}
\beta \ \gamma \ \delta \ \epsilon \ \cdots \ \eta \ \alpha \\
\gamma \ \alpha \ \beta \ \delta \ \cdots \ \zeta \ \eta
\end{pmatrix} \]

another circular substitution degree \( p \), and as it is contiguous to the first, these two substitutions acting successively will be equivalent to the single substitution:

\[ \begin{pmatrix}
\alpha \ \beta \ \gamma \ \delta \ \cdots \ \zeta \ \eta \\
\gamma \ \alpha \ \beta \ \delta \ \cdots \ \zeta \ \eta
\end{pmatrix} =
\begin{pmatrix}
\alpha \ \beta \ \gamma \\
\gamma \ \alpha \ \beta
\end{pmatrix} . \]

So if the first two substitutions do not change the value \( K_1 \) of the function \( K \), this value will not be changed by the circular substitution of the third degree

\[ \begin{pmatrix}
\alpha \ \beta \ \gamma \\
\gamma \ \alpha \ \beta
\end{pmatrix} . \]

It follows that if the value of \( K_1 \) is not changed by any of the circular substitutions of degree \( p \), then it cannot be changed by any circular substitutions of degree three; it only remains to develop the consequences of the latter situation.

If one designates by the name transposition a circular substitution of the second degree, such as \( \Large \bigl(\begin{smallmatrix} \alpha \ \beta \\ \beta \ \alpha \end{smallmatrix}\bigr) \), or, equivalently, an operation which exchanges two indices \( \alpha \) and \( \beta \) and which we indicate by \( (\alpha, \beta) \), then each circular substitution of the third degree is equivalent to two transpositions successively applied. Thus, for example, the substitution

\[ \begin{pmatrix}
\alpha \ \beta \ \gamma \\
\gamma \ \alpha \ \beta
\end{pmatrix} \]

will be equivalent to the product of two contiguous substitutions,

\[ \begin{pmatrix}
\alpha \ \beta \ \gamma \\
\beta \ \alpha \ \gamma \
\end{pmatrix}
\begin{pmatrix}
\beta \ \alpha \ \gamma \\
\gamma \ \alpha \ \beta
\end{pmatrix} , \]

which can also be represented by

\[ (\alpha, \beta), (\beta, \gamma). \]

So if the value \( K_1 \) is not changed by the circular substitution \( \Large \bigl(\begin{smallmatrix} \alpha \ \beta \ \gamma\\ \beta \ \gamma \ \alpha \end{smallmatrix}\bigr) \), the same value will not be changed by the transpositions \( (\alpha, \beta), (\beta, \gamma) \) applied successively; and therefore the transposition \( (\alpha, \beta) \) will not change \( K_1 \) to \( K_2 \) unless at the same time transposition \( (\beta, \gamma) \) changes \( K_2 \) into \( K_1 \) and therefore also \( K_1\) into \( K_2 \); so the two transpositions \( (\alpha, \beta), (\beta, \gamma) \), which have the index \( \beta \) in common, give the same result \( K_2 \) when applied to \( K_1 \). We'll see if the same value \( K_1 \) is not changed by the circular substitution of the third degree:

\[ \begin{pmatrix}
\beta \ \gamma \ \delta \\
\delta \ \beta \ \gamma
\end{pmatrix} . \]

Then the transpositions \( (\beta, \gamma) \) and \( (\gamma, \delta) \), which have the common index \( \gamma \), both change \( K_1 \) into \( K_2 \). As a result, the transpositions

\[ (\alpha, \beta), (\gamma, \delta), \]

which have no common indices, still lead to the same result.

It follows from what has just been said, that if the value \( K_1 \) of the function \( K \) cannot be changed by any of the third-degree circular substitutions made ​​among the indices \( 1, 2, 3, \cdots n \), and that we represent as \( K_2 \) the value is derived from \( K_1 \) by the transposition \( (1, 2) \), then all other transpositions will change \( K_1 \) to \( K_2 \) and consequently \( K_2 \) to \( K_1 \). Accordingly, two successive transpositions do not change the value \( K_1 \). Thus, in the event that one considers the number of different values ​​of the function \( K \), values ​​that can always be derived from \( K_1 \) by transpositions operating on indices \( 1, 2, 3, \cdots n \), it is at most equal to \( 2 \); moreover, it could be reduced to one only in the case where this function becomes symmetric. This proves that if the function \( K \) is not symmetric, then the number of its values ​cannot be less than \( p \), without being equal to \( 2 \).

For example, excluding the symmetric functions and those that have only two values, one finds that a function of the fifth or sixth order cannot take less than five values; a function of the seventh, eighth, ninth or tenth order less than seven values; a function of the eleventh or twelfth order, less than thirteen values, and so on. Moreover, assuming that \( n = 3 \) or \( n = 4 \), one has \( p = 3 \), and it is seen from the previous theorem that the third and fourth order does not rule out functions with three values.

When the order of the function is itself a prime number, one has \( p = n \); thus, any function whose order is a prime number cannot take fewer values than the number of variables, provided that functions without more than two variables are excluded.

Besides, it is not always possible to lower the index​​, that is to say, the number of values ​​of a function, to the limit that we have just assigned; and if one excepts functions of the fourth order that can take three values, I do not know of any non-symmetric functions whose index is less than the order, other than for index \( 2 \). The above theorem shows at least that such functions do not exist when the order of the function is a prime number, since then the limit found is the same as that number. You can still prove this assertion for \( n = 6 \) by showing that a function of six letters cannot take less than six values, assuming it has more than two. This is done with the help of the following considerations.

Let \( K \) be a function of the sixth order and denote by \( 1, 2, 3, 4, 5, 6 \), the indices of the six variables; the total number of possible values ​​of the function \( K \) will be equal to the product:

\[ 1.2.3.4.5.6 = 720. \]

Let now \( \alpha, \beta, \gamma \) be three of six indexes taken at will, and \( K_1 \) a value ​​of \( K \). The number of permutations that can be formed with the three indices \( \alpha, \beta, \gamma \) will equal the product:

\[ 1.2.3 = 6. \]

and one can always derive from the value \( K_1 \) five other values ​​of the function \( K \) through transposition or circular substitutions of the third degree made ​​between the indices \( \alpha, \beta, \gamma \). Let

\[ K_2, K_3, K_4, K_5, K_6 \]

be the new values ​​in question; the six values

\[ K_1, K_2, K_3, K_4, K_5, K_6 \]

are all different from each other, or else will be equal two by two, three by three, or all equal. In the first case, the number of different values ​​of the given function will equal at least \( 6 \). In the three other cases, at least one of the values

\[ K_2, K_3, K_4, K_5, K_6 \]

will be equal to \( K_1 \); and therefore, one can, without altering the value \( K_1 \), exchange two or three of the indices \( \alpha, \beta, \gamma \) by means of a simple transposition or by means of a circular substitution of the third degree.

Suppose now that one divides six indexes \( 1, 2, 3, 4, 5, 6 \) into groups so as to include in the same group two indices that are both at once either in a transposition or in a circular substitution of the third degree that does not change the value \( K_1 \). According to the above, for the particular function to have ​​less than six values, it is necessary that, for the three indices \( \alpha, \beta, \gamma \) taken at will, at least two are included in the same group; and in this case, one can obviously form only two different groups, and one of these two groups may be composed of a single index. It remains to be seen how the function \( K \) can get different values when the number of groups formed is equal to \( 2 \) and when that number is reduced to \( 1 \); the order established among three randomly chosen indices will be inverted in a certain way, without the value \( K_1 \) being altered.

Assume first that the indices are divided into two groups. Let \( \alpha, \beta \) be two indexes taken from one of the groups and \( \gamma \) an index from the other group. Since one can exchange two of the three indexes without changing the value \( K_1 \), and the index \( \gamma \) cannot be exchanged with one of the other two, it is clear that the value \( K_1 \) will not be altered by transposition \( (\alpha, \beta) \). As a result, the value cannot be changed by any substitutions made ​​between the indices of the same group; but it would be altered by substitutions and transpositions moving some of the indices of one group with indices from inside another group: one can even ensure that two values ​​of \( K \), where the composition of the two groups is different, are certainly unequal; because if they weren't, then the values ​​of \( K \) for the various ways in which one can compose the two groups in question, would be equal two by two, three by three, and so on, or all equal to each other. One of them would be equal to the value \( K_1 \) of the function \( K \), and in relation to the same value, there would be several ways to compose the two groups, which is absurd. Thus, to obtain the different values, it suffices to traverse in succession all the indices of one group in the other, or exchange the two groups altogether. That said, one obtains the following results.

If one of the groups consists of five indices and the other one; one traverses successively in the latter group each of the indices \( 1, 2, 3, 4, 5, 6 \), obtaining a total of six different values ​​of the function \( K \).

If one of the groups consists of four indices, and the other two; one traverses successively in the latter group all combinations of the six indices, taken in pairs, to get in all fifteen different values ​​of the function.

Finally, if the two groups are each formed of three indices, and one cannot exchange these two groups; then traversing successively in one of them all combinations of indices taken three by three, one obtains a total of twenty different values ​​of the given function. The number of these values ​​would be halved and reduce to ten if one could exchange the two groups, that is to say, substitute at the same time all the indices of the first group with the second, and vice versa.

So when the indices can be divided into two groups, so that the transposition of two indices included in a group do not change the value \( K_1 \), the number of different values ​​that the function \( K \) can take is necessarily one of these:

\[ 6, 15, 20, 10. \]

To provide examples of these different cases, it is sufficient to cite the following four functions,

\[ a_1 a_2 a_3 a_4 a_5 + a_6 \\
a_1 a_2 a_3 a_4 + a_5 a_6 \\
a_1 a_2 a_3 + 2a_4 a_5 a_6 \\
a_1 a_2 a_3 + a_4 a_5 a_6. \]

In each of these functions, the indices are divided into two groups; when included together in the same group, those transpositions or third-degree circular substitutions do not change the value of the function. Let us now see what would happen if all the indices were brought back in one group.

In the latter case, given a circular substitution of the second or third degree that does not change the value \( K_1 \) of the function \( K \), one can always find another substitution of the same type that does not change the value, which has one or two indices in common with the first. That said, it is easy to see that all transpositions acting on \( K \) between two indices taken at will in the two substitutions in question, will lead to the same value of the function \( K \). And indeed, if the two substitutions in question have two common indices \( \alpha \) and \( \beta \), it may happen that one of them is of the second degree and the other of the third, or they are both third degree. In the first case, they may be represented by

\[ \Biggl( \begin{matrix}
\alpha \ \beta \\
\beta \ \alpha
\end{matrix} \Biggr) ,
\left( \begin{matrix}
\alpha \ \beta \ \gamma \\
\beta \ \gamma \ \alpha
\end{matrix} \right) , \]

where \( \gamma \) is the third index; and since the second does not change the value \( K_1 \), we shall prove by reasoning similar to that we have already made ​​in such circumstances that the three substitutions or transpositions

\[ (\alpha, \beta), (\alpha, \gamma), (\beta, \gamma) \]

give the same value of \( K \). In the second case, the two substitutions may be represented by:

\[ \begin{pmatrix}
\alpha \ \beta \ \gamma \\
\beta \ \gamma \ \alpha
\end{pmatrix} ,
\Biggl( \begin{matrix}
\alpha \ \beta \ \delta \\
\beta \ \delta \ \alpha
\end{matrix} \Biggr) , \]

where \( \gamma \) and \( \delta \) are two new indices. Under the first, the three transpositions

\[ (\alpha, \beta), (\alpha, \gamma), (\beta, \gamma) \]

give the same value of \( K \). Under the second, the three transpositions

\[ (\alpha, \beta), (\alpha, \delta), (\beta, \delta) \]

will also give the same value of \( K \); and as transposition \( (\alpha, \beta) \) can only give a single value of \( K \); it follows that the five transpositions

\[ (\alpha, \beta), (\alpha, \gamma), (\beta, \gamma), (\alpha, \delta), (\beta, \delta) \]

lead to the same result.

Now suppose that the two substitutions have a single index in common. It may happen that the two substitutions are of the second degree, or one of the second degree and one of the third, or both are of the third degree.

To give an example of the first case, let:

\[ \Biggl( \begin{matrix}
\alpha \ \beta \\
\beta \ \alpha
\end{matrix} \Biggr) ,
\begin{pmatrix}
\alpha \ \gamma \\
\gamma \ \alpha
\end{pmatrix} , \]

be two substitutions that do not change the value \( K_1 \): these two substitutions are equivalent to the two transpositions \( (\alpha , \beta), (\alpha , \gamma) \); and as, by virtue of the first, one can pass over the index \( \beta \) in place of the index \( \alpha \) without moving the index \( \gamma \), it is clear that the indices \( \beta \) and \( \gamma \) will have the same properties respectively as the indices \( \alpha \) and \( \gamma \), such that the transposition

\[ (\beta, \gamma) \]

will not change the value \( K_1 \).

Let, in the second case,

\[ \Biggl( \begin{matrix}
\alpha \ \beta \\
\beta \ \alpha
\end{matrix} \Biggr) ,
\begin{pmatrix}
\alpha \ \gamma \ \delta \\
\gamma \ \delta \ \alpha
\end{pmatrix} , \]

be two given substitutions; one can, by executing once or twice in a row the second substitution, successively replace the index \( \gamma \) and the index \( \delta \) in place of the index \( \alpha \) without moving the index \( \beta \). For example, the following three transpositions

\[ (\alpha, \beta), (\beta, \gamma), (\beta, \delta) \]

will not change the value \( K_1 \); and in conclusion, as in the previous case, the transpositions

\[ (\alpha, \gamma), (\alpha, \delta), (\gamma, \delta) \]

do not change as well.

Finally, in the third case, let

\[ \Biggl( \begin{matrix}
\alpha \ \beta \ \gamma \\
\beta \ \gamma \ \alpha
\end{matrix} \Biggr) ,
\Biggl( \begin{matrix}
\alpha \ \gamma \ \delta \\
\gamma \ \delta \ \alpha
\end{matrix} \Biggr) , \]

be two given substitutions; one can, by executing once or twice in a row the second substitution, successively place the indices \( \delta \) and \( \epsilon \) in place of the index \( \alpha \) without moving the indices \( \beta \) and \( \gamma \); and one concludes that the substitutions

\[ \begin{pmatrix}
\alpha \ \beta \ \gamma \\
\beta \ \gamma \ \alpha
\end{pmatrix} , \]

\[ \begin{pmatrix}
\delta \ \beta \ \gamma \\
\beta \ \gamma \ \delta
\end{pmatrix} , \]

\[ \begin{pmatrix}
\epsilon \ \beta \ \gamma \\
\beta \ \gamma \ \epsilon
\end{pmatrix} , \]

do not change the value \( K_1 \); for example, the transpositions between any two of the indices \( \alpha, \beta, \gamma, \delta, \epsilon \) give the same value to the function \( K \).

If one extends the step-by-step reasoning we just made to ​​the indices of any substitutions, which, in theory, do not change the value \( K_1 \), we conclude that the transpositions performed on \( K_1 \) with the six indices \( 1, 2, 3, 4, 5, 6 \), taken in pairs, all lead to the same value of the function \( K \), which we denote by \( K_2 \); consequently \( K_1 \) retains the same value after an even number of successive transpositions, and changes value after an odd number of transpositions. The function will have two values if \( K_1 \) and \( K_2 \) are different from each other; one value if they are the same: that is to say, it becomes symmetric if:

\[ K_2 = K_1. \]

Summarizing what has been said above, it is seen that a function of the sixth order can have no fewer than six values, unless the number of these values is \( 2 \) or \( 1 \).

All the theorems stated in this paper would still subsist even if some of the variables contained in these functions that are considered are multiplied by zero; but then these last variables dropping out, to determine the order of each function, it would be necessary to focus not on the number of variables it contains, but on the number of these variables augmented by the number of those that we can substitute in their place. For example, if one denotes by \( a_1, a_2, a_3, a_4 \) the four roots of an equation of the fourth degree, the quantity

\[ a_2 + a_4, \]

considered as a function of these roots, will be of the fourth order, and this function will take six values ​​that will be respectively

\[ a_1 + a_2, \;\; a_1 + a_3, \;\; a_1 + a_4, \;\; a_2 + a_3, \;\; a_2 + a_4, \;\; a_3 + a_4. \]

It will perhaps be useful to mention here the conditions which a function must satisfy, so that the number of its values ​​is reduced to \( 2 \). Let \( K \) be a function of this nature, and denote by \( K_1, K_2 \) the two values ​​in question. The number of these values ​​being equal to \( 2 \), and therefore less than \( 6 \), if the indices contained in the function are divided into several groups, so as to contain in the same group two indices that are at the same time within either a transposition or a circular substitution of the third degree that does not change the value \( K_1 \); then we will see, as above, taking three indices chosen at will, at least two will be included in the same group, from which it follows that we can form no more than two different groups. Moreover, applying the reasoning already used here, it develops that the number of groups can not be equal to \( 2 \), unless the different values ​​of the function determined by the different ways in which one can compose these two groups swapping the indices with one another, are all unequal; and in this case, the number of function values ​​would be necessarily greater than \( 2 \), contrary to hypothesis. As a result, for this hypothesis to hold, it is necessary that all the indices are contained in a single group; from which one can conclude, using the theory presented above, that \( K_1 \) must retain the same sign after an even number of transpositions of indices, and become \( K_2 \) after an odd number of transpositions. For example, any function such as the following:

\[ (a_1 - a_2)(a_1 - a_3) \cdots (a_1 - a_n)(a_2 - a_3) \cdots (a_2 - a_n) ... (a_{n-1} - a_n) \]

can only acquire two equal values ​with ​opposite signs, always keeping the same sign after an even number of transpositions of indices, always changing sign after an odd number of transpositions; from which it follows that each of its terms subject to transpositions, considered alternatively, receive the plus sign and the minus sign.

- finis -

---

Translated by Mike Bertrand and Stephen Gaschignard (Dec 13, 2014).