The Calculus of Finite Differences

Progressive differences of the first few cubes.

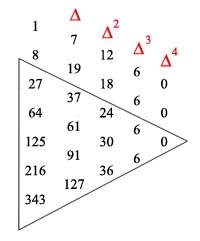
Write down the first few cubes, then put their differences \( \Delta \) in the second column, the differences of those differences \( \Delta^2 \) in the third column, and so on. Remarkably, \( \Delta^3 = 6 \), and that is true for any contiguous sequence of cubes (obviously \( \Delta^4 = 0 \)). Do that with the fourth powers and you find that \( \Delta^4 = 24, \) and in general for contiguous \( n^{th} \) powers, \( \Delta^n = n!. \) The key to unlocking this mystery is the Calculus of Finite Differences, out of vogue now apparently, but with a hallowed history going back to Newton and before and studied in depth by George Boole in 1860.^[1] His book can still be read with profit, as can C. H Richardson's little text from 1954. ^[2]

Euler used \( \Delta^n x^n = n! \) in 1755 to prove the two squares theorem. Boole and those following him employed the term "calculus" advisedly, many theorems in the finite case matching similar ones in the familiar infinitesimal calculus. Which stands to reason, considering all there is in common, it's just that now \( \Delta x = 1. \)

Following Boole, denote a real function, or perhaps one just defined on the integers, by \( U_x \) rather than the standard \( U(x) \) — \( U_x = x^3, \) for example. Then define \( \Delta U_x = {U_{x + 1} - U_x}. \) For example:

\[ \begin{align*}
{\Delta x^2} &= {{(x+1)}^2 - x^2} &&= {2x + 1,} \\
{\Delta x^3} &= {{(x+1)}^3 - x^3} &&= {3x^2 + 3x + 1,} \\
{\Delta a^x} &= {a^{x+1} - a^x} &&= {(a-1)a^x.}
\end{align*} \]

The following theorems are from Richardson (p. 7-8):

Theorem 1. If \( c \) is a constant, \( \Delta c = 0. \)

Theorem 2. \( \Delta^n(U_x \pm V_x) = {\Delta^n U_x \pm \Delta^n V_x}. \)

Theorem 3. If \( c \) is a constant, \( \Delta^n(c U_x) = {c \Delta^n U_x}. \)

Theorem 3'. If \( p_x \) is a polynomial, then \( \text{deg} (\Delta p_x) = \text{deg} (p_x) - 1. \)

Theorem 1 is obvious and Theorems 2 and 3 almost so by applying \( \Delta \) repeatedly. For Theorem 3', note that:

\[ \begin{equation}{\Delta x^m = {{(x + 1)}^m - x^m} = {mx^{m-1} + {{m(m-1)} \over 2!} x^{m-2} + \cdots + mx + 1 }.} \tag{1} \end{equation} \]

Since a polynomial \( p_x \) is a linear combination of \( x^m \)s, Theorems 1 — 3 with \( n = 1 \) imply Theorem 3'. Now with little fuss we have the result mentioned above:

Theorem 4. \( \Delta x^n = n! \) when \( n \) is a positive integer.

Proof. Take the differences of \( x^n, \) then the differences of the differences, and so on. \( \Delta x^n \) is just (1) with \( m = n. \) Write it this way:

\[ \Delta x^n = {n x^{n-1} + \text{polynomial of degree} \; n - 2}. \]

\[ \begin{align*}
\therefore \Delta^2 x^n &= \Delta({n x^{n-1} + \text{polynomial of degree} \; n - 2)} \\
&= n \Delta x^{n-1} + \Delta(\text{polynomial of degree} \; n - 2) \\
&= n [{(n-1) x^{n-2} + \text{polynomial of degree} \; n - 3}] + \text{polynomial of degree} \; n - 3 \\
&= n (n-1) x^{n-2} + \text{polynomial of degree} \; n - 3.
\end{align*} \]

Continue to take differences. At each step, the degrees of the polynomials in each summand decrease by one and a new multiplier comes in for the first summand: \( (n-2), (n-3), \) and so on, eventually reducing to \( \Delta x^n = n!. \) QED.

Let \( n \) be a positive integer and take successive forward differences:

\[\Delta = \left\{
\begin{array}{lr}
(n+1)^3 - n^3 \\
(n+2)^3 - (n+1)^3 \\
(n+3)^3 - (n+2)^3
\end{array}
\right.
\]

\[\Delta^2 = \left\{
\begin{array}{lr}
[(n+2)^3 - (n+1)^3] - [(n+1)^3 - n^3] \\
[(n+3)^3 - (n+2)^3] - [(n+2)^3 - (n+1)^3]
\end{array}
\right.
\]

\[ \Delta^3 = (n+3)^3 - 3(n+2)^3 + 3(n+1)^3 - n^3. \]

The appearance of the binomial coefficients here is not coincidental, arising from the way the differences are formed. Recasting and bringing in Theorem 4:

\[ {\sum_{k=0}^3 (-1)^{k+1} {3 \choose k} (n+k)^3} = 3! = 6. \]

In fact there is nothing special about \( 3 \), the general version for positive integer \( m \) being:

\[ {\sum_{k=0}^m (-1)^{k+1} {m \choose k} (n+k)^m} = m!. \]

Taking \( n = 0, \) for example:

\[ {\sum_{k=0}^m (-1)^{k+1} {m \choose k} k^m} = m!, \]

which sums the first \( m \) powers, but alternating the signs and weighting with binomial coefficients. Put \( m = 5 \) in this last expression to see the kind of thing:

\[ \begin{align*}
{\sum_{k=0}^5 (-1)^{k+1} {5 \choose k} k^5} &= -1 \cdot 0^5 + 5 \cdot 1^5 - 10 \cdot 2^5 + 10 \cdot 3^5 - 5 \cdot 4^5 + 1 \cdot 5^5 \\
&= 5 -320 + 2430 -5120 +3125 \\[0.7ex]
&= 120 = 5!.
\end{align*} \]

If \( n \neq 0 \) those powers become large quickly, but in such a way as to mostly offset. Try to prove these identities any other way!

The Maclaurin series for a polynomial is finite, having as many terms as the degree of the polynomial:

\[ f(x) = {f(0) + f'(0)x + {f''(0) \over 2!} x^2 + {f'''(0) \over 3!} x^3 + \cdots + {f^{(n)}(0) \over n!} x^n}. \]

Amazingly, there is a finite difference version defined in terms of the factorial function:

\[ x^{(n)} = x(x-1)(x-2) \cdots (x - n + 1). \]

Note there are as many factors as the value of the exponent and the degree is \( n, \) just like with ordinary powers, and they difference like powers differentiate:

\[ \begin{align*}
\Delta x^{(n)} &= {(x+1)}^{(n)} - x^{(n)} \\[0.7ex]
&= (x+1)(x)(x-1) \cdots (x-n+2) - (x)(x-1) \cdots (x-n+1) \\[0.7ex]
&= \big[(x+1) - (x-n+1)\big](x)(x-1) \cdots (x-n+2) \\[0.7ex]
&= n x^{(n-1)}.
\end{align*} \]

The Newton series is strictly analogous and is proven in the same way, by progressive differencing and coefficient assignment, the key being that the formula for differencing factorials is identical to that for differentiating powers, as just pointed out. Here is the Newton series for a polynomial \( U_x: \)

\[ \begin{equation}{U_x = {U_0 + \Delta U_0 x^{(1)} + \Delta^2 U_0 {x^{(2)} \over 2!} + \Delta^3 U_0 {x^{(3)} \over 3!} + \cdots + \Delta^n U_0 {x^{(n)} \over n!}}.} \tag{2} \end{equation} \]

Newton's work on finite difference is legendary and a germinal version of (2) appears in the Principia in order to interpolate cometary positions. According to Herman Goldstine ^[3], a foremost authority on this subject, Thomas Harriot and the logarithmic genius Henry Briggs anticipated Newton (p. 70), and James Gregory virtually put (2) in its now canonical form (p. 75). The \( \Delta \)s at \( 0 \) for a given polynomial in (2) are easily calculated, enabling the polynomial to be expressed in terms of factorials. Then the Newton series can be used to interpolate a set of data points with a polynomial or (what amounts to the same thing) find a polynomial formula fitting the data points. Suppose we want a polynomial formula for \( U_x \), for example, where \( U_0 = 5, \; U_1 = 4, \; U_2 = 5 \) and \( U_3 = 14. \) First build the differences table:

\[ \begin{array}{l|cr}
x & U_x & \Delta U_x & \Delta^2 U_x & \Delta^3 U_x \\
\hline
\color{red}{0} & \color{red}{5} & \color{red}{-1} & \color{red}{2} & \color{red}{6} \\
1 & 4 & 1 & 8 \\
2 & 5 & 9 \\
3 & 14
\end{array} \]

Plugging into the Newton series:

\[ \begin{align*}
U_x &= U_0 + \Delta U_0 x^{(1)} + \Delta^2 U_0 {x^{(2)} \over 2!} + \Delta^3 U_0 {x^{(3)} \over 3!} \\[0.7ex]
&= \color{red}{5} \color{red}{-1} \cdot x^{(1)} + {\color{red}{2} \over 2!} x^{(2)} + {\color{red}{6} \over 3!} x^{(3)} \\[0.7ex]
&= 5 - x + x(x-1) + x(x-1)(x-2) \\[0.7ex]
&= 5 - x + (x^2 - x) + (x^3-3x^2+2x) \\[0.7ex]
&= x^3 - 2x^2 + 5
\end{align*} \]

If thinking of this as a formula-finding exercise for the sequence whose first four terms are \( a_0 = 5, a_1 = 4, a_2 = 5, a_3 = 14,\; a_n = n^3 - 2 n^2 + 5 \) fits the bill.

Suppose \( V_x \) is a function whose difference is \( U_x. \) By definition, \( \Delta V_x = U_x, \) and we put \( V_x = \Delta^{-1} U_x. \) Since \( U_x = V_{x+1} - V_x \) for all \( x \):

\[ \begin{align*}
U_0 &= V_1 - V_0 \\
U_1 &= V_2 - V_1 \\
U_2 &= V_3 - V_2 \\
\vdots \\
U_n &= V_{n+1} - V_n
\end{align*} \]

A telescoping effect shrinks the differences on the right when adding these equations: \( \sum_{k=1}^n U_k = {V_{n+1} - V_0} = \left.V_x\right|_0^{n+1} = \left.\Delta^{-1}U_x\right|_0^{n+1}. \) As the formulas suggest, anti-differencing is summing, just as anti-differentiating is integrating. Let's start with an easy example from Richardson (p 26, Ex 2), to find a formula for:

\[ S_n = 1 \cdot 2 + 2 \cdot 3 + 3 \cdot 4 + \cdots + n(n+1). \]

Here \( U_x = x(x+1) = (1+x)^{(2)}\) and a calculation virtually identical to definite integration can be carried out, considering that \( \Delta (1+x)^{(3)} = 3 (1+x)^{(2)} \) and so \( \Delta^{-1} (1+x)^{(2)} = {1 \over 3} (1+x)^{(3)}: \)

\[ \begin{align*}
S_n &= \sum_{k=1}^n U_k \\[0.7ex]
&= \sum_{k=1}^n (1+k)^{(2)} \\[0.7ex]
&= \left. \Delta^{-1} (1+k)^{(2)} \right|_1^{n+1} \\[0.7ex]
&= \textstyle \left. {1 \over 3}(1+k)^{(3)} \right|_1^{n+1} \\[0.7ex]
&= \textstyle {1 \over 3} [(n+2)^{(3)} - 2^{(3)}] \\[0.7ex]
&= \textstyle {1 \over 3} n(n+1)(n+2).
\end{align*} \]

The difference of a product is easily calculated by expanding each side of:

\[ \Delta (U_x V_x) = U_x \cdot \Delta V_x + V_{x+1} \cdot \Delta U_x. \]

Transposing and anti-differencing (integrating) leads to the formula for finite integration by parts:

\[ \Delta^{-1} (U_x \cdot \Delta V_x) = U_x V_x - \Delta^{-1} (V_{x+1} \cdot \Delta U_x). \]

Integration by parts enables summation of more complex expressions beyond polynomials, like \( S_n = \sum_{k=1}^n k 3^k \) (Richardson, p 29, Ex 1). Using \( k \) instead of \( x \), put

\[ U_k = k, \hskip{30px} \Delta V_k = 3^k. \]

\[ \textstyle \therefore \Delta U_k = 1, \hskip{30px} V_k = \Delta^{-1} 3^k = {1 \over 2} 3^k, \]

\[ \textstyle V_{k+1} = {1 \over 2} 3^{k+1} = {3 \over 2} 3^k. \]

We'll also need:

\[ \begin{align*}
\Delta^{-1}(V_{k+1} \cdot \Delta U_k) &= \Delta^{-1} ({3 \over 2} 3^k \cdot 1) \\[0.7ex]
&= {3 \over 2} \Delta^{-1} 3^k \\[0.7ex]
&= {3 \over 2} \cdot {3^k \over 2}
\end{align*} \]

Proceed to apply integration by parts:

\[ \begin{align*}
S_n &= \sum_{k=1}^n k 3^k \\[0.7ex]
&= \left. \Delta^{-1} (U_k \cdot \Delta V_k) \right|_1^{n+1} \\[0.7ex]
&= [U_k V_k - \Delta^{-1} (V_{k+1} \cdot \Delta U_k)]_1^{n+1} \\[0.7ex]
&= \left[k \cdot {3^k \over 2} - {3 \over 2} \cdot {3^k \over 2}\right]_1^{n+1} \\[0.7ex]
&= \textstyle \left[{1 \over 4} \cdot 3^k \cdot (2k-3)\right]_1^{n+1} \\[0.7ex]
&= \textstyle {1 \over 4} \cdot 3^{n+1} \cdot (2(n+1)-3) - {1 \over 4} \cdot 3^1 \cdot (2 \cdot 1 - 3) \\[0.7ex]
&= \textstyle {1 \over 4} \cdot 3^{n+1} \cdot (2n-1) + {3 \over 4}. \\
\end{align*} \]

What would you do with a nasty sum like \( \sum_{i=1}^n \sum_{j=1}^n (i+j)^2 \)? The very words of David Gleich, from whose work this example is taken. Perhaps unsurprisingly, this sum devolves to a polynomial in \( n, \) which could be nailed down using a Newton series, or you could expand the square within the summation signs, leading to simpler sums. But here is another approach using finite integration. Note we are using \( \Delta^{-1} (u + c)^{(n)} = {1 \over {n+1}} (u + c)^{(n+1)} \), also that \( u^2 = u^{(2)} + u^{(1)}: \)

\[ \begin{align*}
S_n &= \sum_{i=1}^n \sum_{j=1}^n (i+j)^2 \\
&= \sum_{i=1}^n \sum_{j=1}^n \left((i+j)^{(2)} + (i+j)^{(1)}\right) \\
&= \Delta_i^{-1} \left[ \Delta_j^{-1} \left[(i+j)^{(2)} + (i+j)^{(1)}\right]_{j=1}^{n+1} \right]_{i=1}^{n+1} \\[0.7ex]
&= \textstyle \Delta_i^{-1} \left[\left({1 \over 3} (i+n+1)^{(3)} + {1 \over 2} (i+n+1)^{(2)}\right) - \left({1 \over 3} (i+1)^{(3)} + {1 \over 2} (i+1)^{(2)}\right)\right]_{i=1}^{n+1} \\[0.7ex]
&= \textstyle \left[{1 \over 4} \cdot {1 \over 3}(2n+2)^{(4)} + {1 \over 3} \cdot {1 \over 2}(2n+2)^{(3)} - \left\{{1 \over 4} \cdot {1 \over 3}(n+2)^{(4)} + {1 \over 3} \cdot {1 \over 2}(n+2)^{(3)} \right\} \right] \\[0.7ex]
&\phantom{{}={}} \textstyle - \left[{1 \over 4} \cdot {1 \over 3}(n+2)^{(4)} + {1 \over 3} \cdot {1 \over 2}(n+2)^{(3)} - \left\{{1 \over 4} \cdot {1 \over 3}2^{(4)} + {1 \over 3} \cdot {1 \over 2}2^{(3)} \right\} \right]. \\
\end{align*} \]

This last monster isn't as bad as it looks. Of the eight terms, the last two involving constants drop out, because each of them includes factors \( (2-2). \) The first two remain as is and the middle four combine into two, with final result:

\[ \begin{align*}
S_n &= \textstyle {1 \over 12}(2n+2)^{(4)} + {1 \over 6}(2n+2)^{(3)} - {1 \over 6} (n+2)^{(4)} - {1 \over 3} (n+2)^{(3)} \\[0.7ex]
&= \textstyle {1 \over 6} n^2 (n+1)(7n+5).
\end{align*} \]

The conversion to standard polynomial notation is courtesy of Wolfram Alpha. Way too much work, you say, but this approach could be used to find \( S_{n,m} = \sum_{i=1}^n \sum_{j=1}^m (i+j)^2 \) with little change and other daunting sums as well, while easier methods might stall.

The calculus of Finite Differences is uncannily like its infinite counterpart, a fact recognized and exploited by investigators. George Boole had this to say in the preface to his highly readable book on the subject published in 1860:

In the following exposition of the Calculus of Finite Differences, particular attention has been paid to the connexion of its methods with those of the Differential Calculus — a connexion which in some instances involves far more than a merely formal analogy.

As recently as the 1950s the finite calculus was taught at university in the United States, initially for actuaries and statisticians, then electrical engineers and physicists too according to Professor Richardson. It's fallen out of favor for some reason, which is a shame considering its beauty and utility. From a strictly logical point of view, it's bizarre that such a deep and sophisticated subject as infinite calculus is taught so early in the curriculum; the finite version would be a great substitute, inherently interesting and useful, yet serving as a gateway for those going on.

There is a small resurgence of interest with the renewed attention to finite matters triggered by computer science. What's old is new, which in and of itself is pleasing to a certain kind of person. Interpolation may not be the life and death subject it was before computers, but it still has its uses. Numerical integration like with the trapezoidal rule is one offshoot, so are Stirling numbers and the gamma function. Generating functions too, beloved by the old analysts according to Boole. The entire subject of the finite calculus goes back centuries, with Newton doing profound and lasting work. It's time for a rebirth.

Mike Bertrand

July 5, 2016

^ 1. A Treatise on the Calculus of Finite Differences, by George Boole (1860).

^ 2. An Introduction to the Calculus of Finite Differences, by C. H. Richardson (1954).

^ 3. A History of Numerical Analysis from the 16^th through the 19^th Century, by Herman H. Goldstine, Springer-Verlag (1977), ISBN 0-387-90277-5.